|
Tent Map
In mathematics, the tent map with parameter μ is the real-valued function ''f''μ defined by :f_\mu(x) := \mu\min\, the name being due to the tent-like shape of the graph of ''f''μ. For the values of the parameter μ within 0 and 2, ''f''μ maps the unit interval , 1into itself, thus defining a discrete-time dynamical system on it (equivalently, a recurrence relation). In particular, iterating a point ''x''0 in , 1gives rise to a sequence x_n: :x_ = f_\mu(x_n) = \begin \mu x_n & \mathrm~~ x_n . The \mu = 2 case of the tent map is the present case of a= \tfrac. A sequence will have the same autocorrelation function as will data from the first-order autoregressive process In statistics, econometrics, and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it can be used to describe certain time-varying processes in nature, economics, behavior, etc. The autoregre ... w_ = (2a-1)w_n + u_ with in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tent Map 2
A tent is a Shelter (building), shelter consisting of sheets of fabric or other material draped over or attached to a frame of poles or a supporting rope. While smaller tents may be free-standing or attached to the ground, large tents are usually anchored using guy ropes tied to stakes or tent pegs. First used as portable homes by nomads, tents are now more often used for recreational camping (recreation), camping and as temporary shelters. Tents range in size from "Bivouac shelter, bivouac" structures, just big enough for one person to sleep in, up to huge circus tents capable of seating thousands of people. Tents for recreational camping fall into two categories. Tents intended to be carried by backpackers are the smallest and lightest type. Small tents may be sufficiently light that they can be carried for long distances on a touring bicycle, a boat, or when backpacking (wilderness), backpacking. The second type are larger, heavier tents which are usually carried in a car or o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean-Pierre Eckmann
Jean-Pierre Eckmann (born 27 January 1944) is a Swiss mathematical physicist in the department of theoretical physics at the University of Geneva and a pioneer of chaos theory and social network analysis.. Eckmann is the son of mathematician Beno Eckmann. He completed his PhD in 1970 under the supervision of Marcel Guenin at the University of Geneva. He has been a member of the Academia Europaea since 2001. In 2012, he became a fellow of the American Mathematical Society. He is also a member of the Göttingen Academy of Sciences and Humanities. With Pierre Collet and Oscar Lanford, Eckmann was the first to find a rigorous mathematical argument for the universality of period-doubling bifurcations in dynamical systems, with scaling ratio given by the Feigenbaum constants. In a highly cited 1985 review paper with David Ruelle, he bridged the contributions of mathematicians and physicists to dynamical systems theory and ergodic theory, put the varied work on dimension-like not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Number
A binary number is a number expressed in the Radix, base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computer, computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thoma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dense Set
In topology and related areas of mathematics, a subset ''A'' of a topological space ''X'' is said to be dense in ''X'' if every point of ''X'' either belongs to ''A'' or else is arbitrarily "close" to a member of ''A'' — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it (see Diophantine approximation). Formally, A is dense in X if the smallest closed subset of X containing A is X itself. The of a topological space X is the least cardinality of a dense subset of X. Definition A subset A of a topological space X is said to be a of X if any of the following equivalent conditions are satisfied: The smallest closed subset of X containing A is X itself. The closure of A in X is equal to X. That is, \operatorname_X A = X. The interior of the complement of A is empty. That is, \operatorname_X (X \setminus A) = \varnothing. Every point in X eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
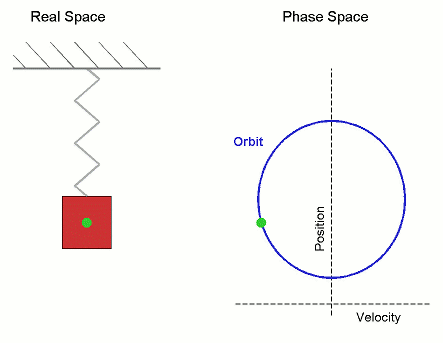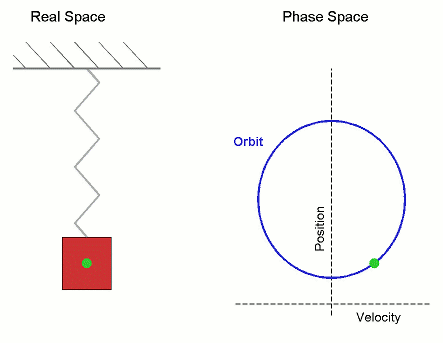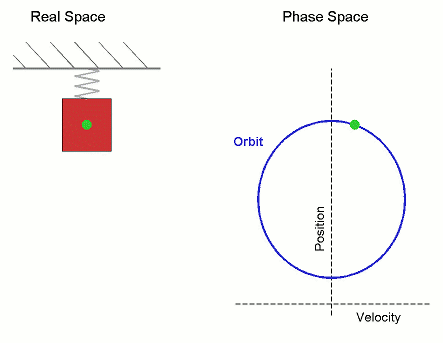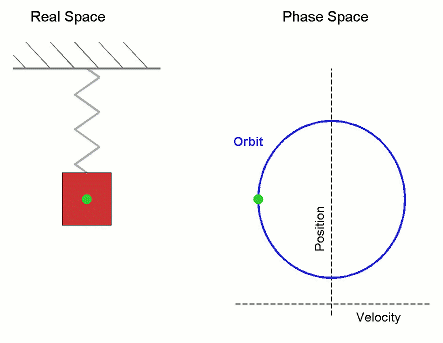
Orbit (dynamics)
In mathematics, specifically in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. It can be understood as the subset of phase space covered by the trajectory of the dynamical system under a particular set of initial conditions, as the system evolves. As a phase space trajectory is uniquely determined for any given set of phase space coordinates, it is not possible for different orbits to intersect in phase space, therefore the set of all orbits of a dynamical system is a partition of the phase space. Understanding the properties of orbits by using topological methods is one of the objectives of the modern theory of dynamical systems. For discrete-time dynamical systems, the orbits are sequences; for real dynamical systems, the orbits are curves; and for holomorphic dynamical systems, the orbits are Riemann surfaces. Definition Given a dynamical system (''T'', ''M'', Φ) with ''T'' a group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julia Set
In complex dynamics, the Julia set and the Classification of Fatou components, Fatou set are two complement set, complementary sets (Julia "laces" and Fatou "dusts") defined from a function (mathematics), function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under iterated function, repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small Perturbation theory, perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaos theory, chaotic". The Julia set of a function is commonly denoted \operatorname(f), and the Fatou set is denoted \operatorname(f). These sets are named after the French mathematicians Gaston Julia and Pierre Fatou whose work began the study of complex dynamics during the early 20th century. Form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root Of 2
The square root of 2 (approximately 1.4142) is the positive real number that, when multiplied by itself or squared, equals the number 2. It may be written as \sqrt or 2^. It is an algebraic number, and therefore not a transcendental number. Technically, it should be called the ''principal'' square root of 2, to distinguish it from the negative number with the same property. Geometrically, the square root of 2 is the length of a diagonal across a Unit square, square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational number, irrational. The fraction (≈ 1.4142857) is sometimes used as a good Diophantine approximation, rational approximation with a reasonably small denominator. Sequence in the On-Line Encyclopedia of Integer Sequences consists of the digits in the decimal expansion of the square root of 2, here truncated to 60 decimal places: : History The Babylonian clay tablet YBC 7289 (–1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation (mathematics), transformation. Specifically, for function (mathematics), functions, a fixed point is an element that is mapped to itself by the function. Any set of fixed points of a transformation is also an invariant set. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain of a function, domain and the codomain of , and . In particular, cannot have any fixed point if its domain is disjoint from its codomain. If is defined on the real numbers, it corresponds, in graphical terms, to a curve in the Euclidean plane, and each fixed-point corresponds to an intersection of the curve with the line , cf. picture. For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |