|
Template Matching
Template matching is a technique in digital image processing for finding small parts of an image which match a template image. It can be used for quality control in manufacturing, navigation of mobile robots, or edge detection in images. The main challenges in a template matching task are detection of occlusion, when a sought-after object is partly hidden in an image; detection of non-rigid transformations, when an object is distorted or imaged from different angles; sensitivity to illumination and background changes; background clutter; and scale changes. Feature-based approach The feature-based approach to template matching relies on the extraction of image features, such as shapes, textures, and colors, that match the target image or frame. This approach is usually achieved using neural networks and deep-learning classifiers such as VGG, AlexNet, and ResNet.Convolutional neural networks (CNNs), which many modern classifiers are based on, process an image by passing it th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landmark Point
In morphometrics, landmark point or shortly landmark is a point in a shape object in which correspondences between and within the populations of the object are preserved. In other disciplines, landmarks may be known as vertices, anchor points, control points, sites, profile points, 'sampling' points, nodes, markers, fiducial markers, etc. Landmarks can be defined either manually by experts or automatically by a computer program. There are three basic types of landmarks: anatomical landmarks, mathematical landmarks or pseudo-landmarks. An anatomical landmark is a biologically-meaningful point in an organism. Usually experts define anatomical points to ensure their correspondences within the same species. Examples of anatomical landmark in shape of a skull are the eye corner, tip of the nose, jaw, etc. Anatomical landmarks determine homologous parts of an organism, which share a common ancestry. Mathematical landmarks are points in a shape that are located according to some ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
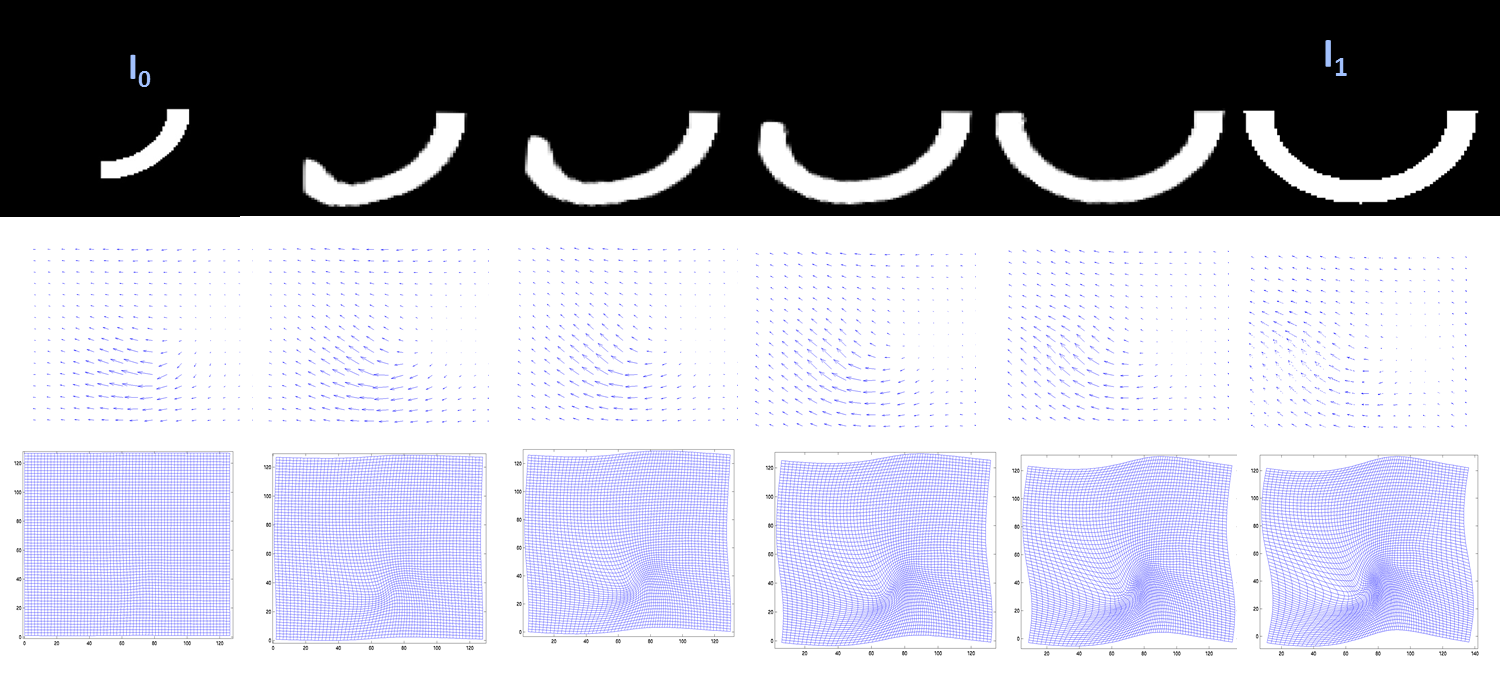
Large Deformation Diffeomorphic Metric Mapping
Large deformation diffeomorphic metric mapping (LDDMM) is a specific suite of algorithms used for diffeomorphic mapping and manipulating dense imagery based on diffeomorphic metric mapping within the academic discipline of computational anatomy, to be distinguished from its precursor based on diffeomorphic mapping. The distinction between the two is that diffeomorphic metric maps satisfy the property that the length associated to their flow away from the identity induces a metric on the group of diffeomorphisms, which in turn induces a metric on the orbit of shapes and forms within the field of computational anatomy. The study of shapes and forms with the metric of diffeomorphic metric mapping is called diffeomorphometry. A diffeomorphic mapping system is a system designed to map, manipulate, and transfer information which is stored in many types of spatially distributed medical imagery. Diffeomorphic mapping is the underlying technology for mapping and analyzing information me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable. Definition Given two differentiable manifolds M and N, a Differentiable manifold#Differentiability of mappings between manifolds, continuously differentiable map f \colon M \rightarrow N is a diffeomorphism if it is a bijection and its inverse f^ \colon N \rightarrow M is differentiable as well. If these functions are r times continuously differentiable, f is called a C^r-diffeomorphism. Two manifolds M and N are diffeomorphic (usually denoted M \simeq N) if there is a diffeomorphism f from M to N. Two C^r-differentiable manifolds are C^r-diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable. Diffeomorphisms of subsets of manifolds Given a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit (control Theory)
The notion of orbit of a control system used in mathematical control theory is a particular case of the notion of orbit in group theory. Definition Let \dot q=f(q,u) be a \ ^\infty control system, where belongs to a finite-dimensional manifold \ M and \ u belongs to a control set \ U. Consider the family =\ and assume that every vector field in is complete. For every f\in and every real \ t, denote by \ e^ the flow of \ f at time \ t. The orbit of the control system \dot q=f(q,u) through a point q_0\in M is the subset _ of \ M defined by :_=\. ;Remarks The difference between orbits and attainable sets is that, whereas for attainable sets only forward-in-time motions are allowed, both forward and backward motions are permitted for orbits. In particular, if the family is symmetric (i.e., f\in if and only if -f\in ), then orbits and attainable sets coincide. The hypothesis that every vector field of is complete simplifies the notations but can be dropped. In this case ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Anatomy
Computational anatomy is an interdisciplinary field of biology focused on quantitative investigation and modelling of anatomical shapes variability. It involves the development and application of mathematical, statistical and data-analytical methods for modelling and simulation of biological structures. The field is broadly defined and includes foundations in anatomy, applied mathematics and pure mathematics, machine learning, computational mechanics, computational science, biological imaging, neuroscience, physics, probability, and statistics; it also has strong connections with fluid mechanics and geometric mechanics. Additionally, it complements newer, interdisciplinary fields like bioinformatics and neuroinformatics in the sense that its interpretation uses metadata derived from the original sensor imaging modalities (of which magnetic resonance imaging is one example). It focuses on the anatomical structures being imaged, rather than the medical imaging devices. It is similar i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pose (computer Vision)
In the fields of computing and computer vision, pose (or spatial pose) represents the position and the orientation of an object, each usually in three dimensions. Poses are often stored internally as transformation matrices. The term “pose” is largely synonymous with the term “transform”, but a transform may often include scale, whereas pose does not. In computer vision, the pose of an object is often estimated from camera input by the process of '' pose estimation''. This information can then be used, for example, to allow a robot to manipulate an object or to avoid moving into the object based on its perceived position and orientation in the environment. Other applications include skeletal action recognition. Pose estimation The specific task of determining the pose of an object in an image (or stereo images, image sequence) is referred to as ''pose estimation''. Pose estimation problems can be solved in different ways depending on the image sensor configuration, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contrast (vision)
Contrast is the difference in luminance or color that makes an object (or its representation in an image or display) visible against a background of different luminance or color. The human visual system is more sensitive to contrast than to absolute luminance; thus, we can perceive the world similarly despite significant changes in illumination throughout the day or across different locations. The maximum contrast of an image is termed the contrast ratio or dynamic range. In images where the contrast ratio approaches the maximum possible for the medium, there is a ''conservation of contrast''. In such cases, increasing contrast in certain parts of the image will necessarily result in a decrease in contrast elsewhere. Brightening an image increases contrast in darker areas but decreases it in brighter areas; conversely, darkening the image will have the opposite effect. Bleach bypass reduces contrast in the darkest and brightest parts of an image while enhancing luminance contr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenspace
In linear algebra, an eigenvector ( ) or characteristic vector is a Vector (mathematics and physics), vector that has its direction (geometry), direction unchanged (or reversed) by a given linear map, linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scalar multiplication, scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative number, negative or complex number, complex number). Euclidean vector, Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation Rotation (mathematics), rotates, Scaling (geometry), stretches, or Shear mapping, shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with nei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |