|
Taylor–Maccoll Flow
Taylor–Maccoll flow refers to the steady flow behind a conical shock wave that is attached to a solid cone. The flow is named after G. I. Taylor and J. W. Maccoll, whom described the flow in 1933, guided by an earlier work of Theodore von Kármán.Von Karman, T., & Moore, N. B. (1932). Resistance of slender bodies moving with supersonic velocities, with special reference to projectiles. Transactions of the American Society of Mechanical Engineers, 54(2), 303-310.Maccoll, J. W. (1937). The conical shock wave formed by a cone moving at a high speed. Proceedings of the Royal Society of London. Series A-Mathematical and Physical Sciences, 159(898), 459-472. Mathematical description Consider a steady supersonic flow past a solid cone that has a semi-vertical angle \chi. A conical shock wave can form in this situation, with the vertex of the shock wave lying at the vertex of the solid cone. If it were a two-dimensional problem, i.e., for a supersonic flow past a wedge, then the incom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shock Wave
In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a medium, but is characterized by an abrupt, nearly discontinuous, change in pressure, temperature, and density of the medium. For the purpose of comparison, in supersonic speed, supersonic flows, additional increased expansion may be achieved through an expansion fan, also known as a Prandtl–Meyer expansion fan. The accompanying expansion wave may approach and eventually collide and recombine with the shock wave, creating a process of destructive interference. The sonic boom associated with the passage of a supersonic aircraft is a type of sound wave produced by Wave interference, constructive interference. Unlike solitons (another kind of nonlinear wave), the energy and speed of a shock wave alone dissipates relatively quickly with distan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theodore Von Kármán
Theodore von Kármán ( , May 11, 1881May 6, 1963) was a Hungarian-American mathematician, aerospace engineer, and physicist who worked in aeronautics and astronautics. He was responsible for crucial advances in aerodynamics characterizing supersonic and hypersonic airflow. The human-defined threshold of outer space is named the " Kármán line" in recognition of his work. Kármán is regarded as an outstanding aerodynamic theoretician of the 20th century. Early life Theodore von Kármán was born into a Jewish family in Budapest, then part of Austria-Hungary, as Kármán Tódor, the son of Helene (Konn or Kohn, ) and . Among his ancestors were Rabbi Judah Loew ben Bezalel, who was said to be the creator of the Golem of Prague, and Rabbi , who wrote about Zohar. His father, Mór, was a well-known educator, who reformed the Hungarian school system and founded Minta Gymnasium in Budapest. He became an influential figure and became a commissioner of the Ministry of Educa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
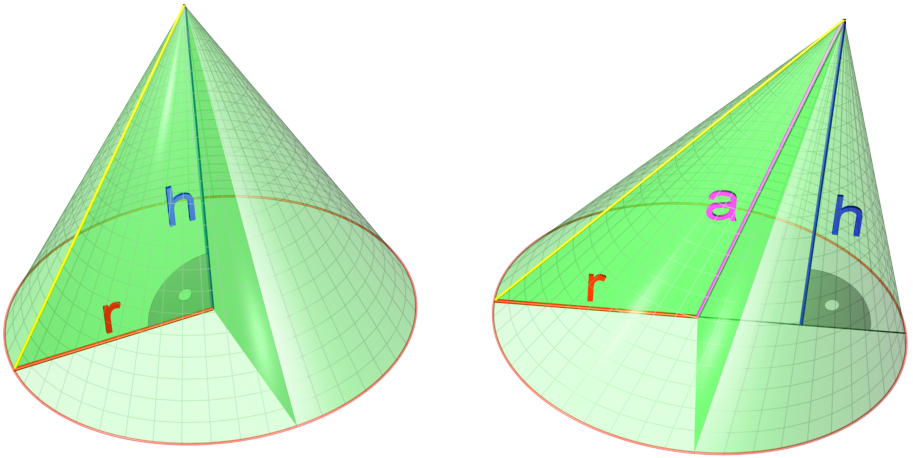
Conical
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supersonic
Supersonic speed is the speed of an object that exceeds the speed of sound (Mach 1). For objects traveling in dry air of a temperature of 20 °C (68 °F) at sea level, this speed is approximately . Speeds greater than five times the speed of sound (Mach 5) are often referred to as hypersonic. Flights during which only some parts of the air surrounding an object, such as the ends of rotor blades, reach supersonic speeds are called transonic. This occurs typically somewhere between Mach 0.8 and Mach 1.2. Sounds are traveling vibrations in the form of pressure waves in an elastic medium. Objects move at supersonic speed when the objects move faster than the speed at which sound propagates through the medium. In gases, sound travels longitudinally at different speeds, mostly depending on the molecular mass and temperature of the gas, and pressure has little effect. Since air temperature and composition varies significantly with altitude, the speed of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shock Polar
The term ''shock polar'' is generally used with the graphical representation of the Rankine–Hugoniot equations in either the hodograph plane or the pressure ratio-flow deflection angle plane. The polar itself is the locus of all possible states after an oblique shock. The shock polar was first introduced by Adolf Busemann in 1929.Busemann, A. 1929. Verdichtungsstosse in ebenen Gasstromungen. In Vortraye aus dem Gebiet der Aerodynamik, Aachen, ed. A. Gilles, L. Hopf, T. von Karman, p. 162. Berlin: Springer-Verlag Shock polar in the (''φ'', ''p'') plane The minimum angle, \theta, which an oblique shock can have is the Mach angle \mu =\sin^(1/M), where M is the initial Mach number before the shock and the greatest angle corresponds to a normal shock. The range of shock angles is therefore \sin^(1/M)\leq\theta\leq\pi /2. To calculate the pressures for this range of angles, the Rankine–Hugoniot equations are solved for pressure: \frac = 1 + \frac \left(M^\sin^\theta - 1\right) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mach Reflection
Mach reflection is a supersonic fluid dynamics effect, named for Ernst Mach, and is a shock wave reflection pattern involving three shocks. Introduction Mach reflection can exist in steady, pseudo-steady and unsteady flows. When a shock wave, which is moving with a constant velocity, propagates over a solid wedge, the flow generated by the shock impinges on the wedge thus generating a second reflected shock, which ensures that the velocity of the flow is parallel to the wedge surface. Viewed in the frame of the reflection point, this flow is locally steady, and the flow is referred to as pseudosteady. When the angle between the wedge and the primary shock is sufficiently large, a single reflected shock is not able to turn the flow to a direction parallel to the wall and a transition to Mach reflection occurs. In a steady flow situation, if a wedge is placed into a steady supersonic flow in such a way that its oblique attached shock impinges on a flat wall parallel to the free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change and information systems including the transmission of information in telecommunication. Entropy is central to the second law of thermodynamics, which states that the entropy of an isolated system left to spontaneous evolution cannot decrease with time. As a result, isolated systems evolve toward thermodynamic equilibrium, where the entropy is highest. A consequence of the second law of thermodynamics is that certain processes are irreversible. The thermodynami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Flow
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity present in the flow. Potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an Conservative vector field#Irrotational vector fields, irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the Curl (mathematics), curl of the gradient of a Scalar (physics), scalar always being equal to zero. In the case of an incompressible flow the velocity potential satisfies Laplace's equation, and potential theory is applicable. However, potential flows also have been used to describe compressible flows and Hele-Shaw flows. The potential flow approach occurs in the modeling of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sound Speed
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. More simply, the speed of sound is how fast vibrations travel. At , the speed of sound in air is about , or in or one mile in . It depends strongly on temperature as well as the medium through which a sound wave is propagating. At , the speed of sound in dry air (sea level 14.7 psi) is about . The speed of sound in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in dry air, deviating slightly from ideal behavior. In colloquial speech, ''speed of sound'' refers to the speed of sound waves in air. However, the speed of sound varies from substance to substance: typically, sound travels most slowly in gases, faster in liquids, and fastest in solids. For example, while sound travels at in air, it travels at in water (almost 4.3 times as fast) and at in iron (almost 15 times as fast). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
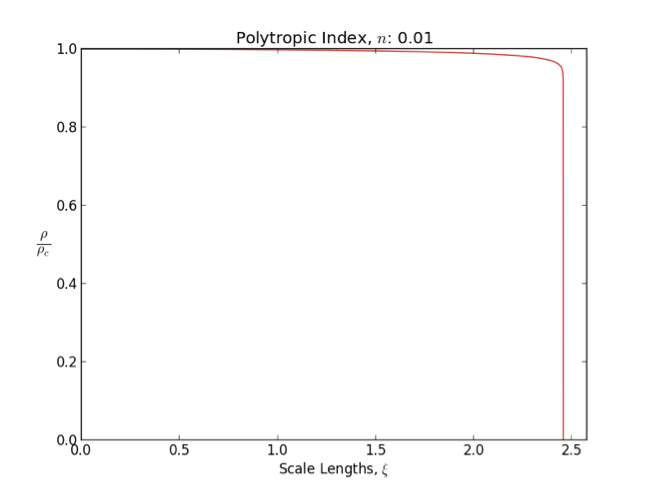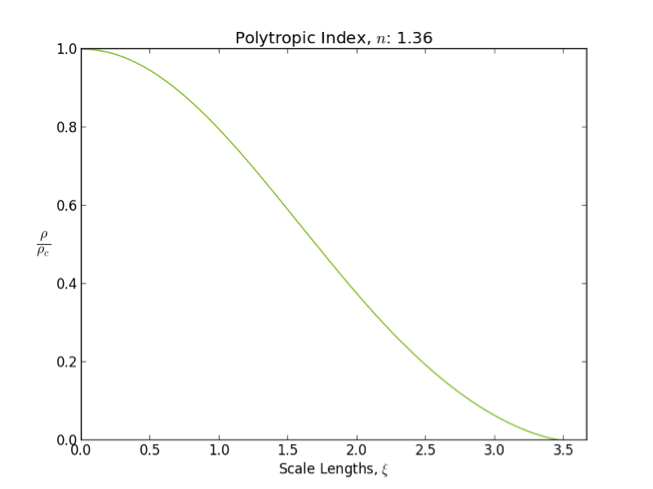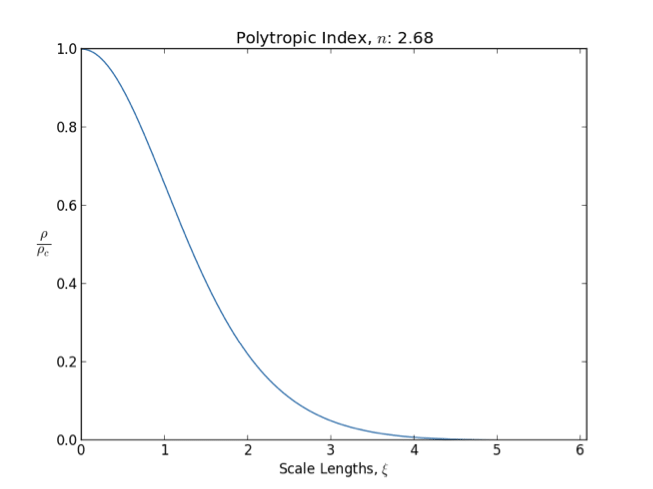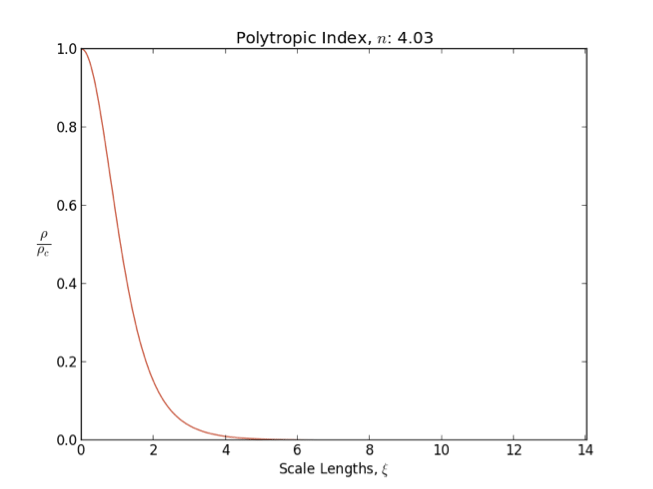
Polytropic Gas
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form P = K \rho^ = K \rho^, where is pressure, is density and is a constant of proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer to an equation of state that looks similar to the ther ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Heat Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the ''isentropic expansion factor'' and is denoted by (gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |