|
Tau Distribution
Tau (; uppercase Τ, lowercase τ or \boldsymbol\tau; ) is the nineteenth letter of the Greek alphabet, representing the voiceless dental or alveolar plosive . In the system of Greek numerals, it has a value of 300. The name in English is pronounced or , but in Greek it is . This is because the pronunciation of the combination of Greek letters αυ can have the pronunciation of either , or , depending on what follows and if a diaeresis is present on the second vowel (see Greek orthography). Tau was derived from the Phoenician letter taw (𐤕). Letters that arose from tau include Roman T and Cyrillic Te (Т, т). Modern usage The lower-case letter τ is used as a symbol for: * Specific tax amount Biology * The expressed period of the freerunning rhythm of an animal, i.e., the length of the daily cycle of an animal when kept in constant light or constant darkness * The dose interval in pharmacokinetics * The core variable in general tau theory * Tau in bioch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Alphabet
The Greek alphabet has been used to write the Greek language since the late 9th or early 8th century BC. It was derived from the earlier Phoenician alphabet, and is the earliest known alphabetic script to systematically write vowels as well as consonants. In Archaic Greece, Archaic and early Classical Greece, Classical times, the Greek alphabet existed in Archaic Greek alphabets, many local variants, but, by the end of the 4th century BC, the Ionia, Ionic-based Euclidean alphabet, with 24 letters, ordered from alpha to omega, had become standard throughout the Greek-speaking world and is the version that is still used for Greek writing today. The letter case, uppercase and lowercase forms of the 24 letters are: : , , , , , , , , , , , , , , , , , , , , , , , The Greek alphabet is the ancestor of several scripts, such as the Latin script, Latin, Gothic alphabet, Gothic, Coptic script, Coptic, and Cyrillic scripts. Throughout antiquity, Greek had only a single uppercas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chronic Traumatic Encephalopathy
Chronic traumatic encephalopathy (CTE) is a neurodegenerative disease linked to repeated trauma to the head. The encephalopathy symptoms can include behavioral problems, mood problems, and problems with thinking. The disease often gets worse over time and can result in dementia. Most documented cases have occurred in athletes involved in striking-based combat sports, such as boxing, kickboxing, mixed martial arts, and contact sports such as rugby union, rugby league, American football, Australian rules football, professional wrestling, and ice hockey. It is also an issue in association football (soccer), but largely as a result of heading the ball rather than player contact. Other risk factors include being in the military ( combat arms), prior domestic violence, and repeated banging of the head. The exact amount of trauma required for the condition to occur is unknown, and as of 2025 definitive diagnosis can only occur at autopsy. The disease is classified as a tauop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Emission
Spontaneous emission is the process in which a Quantum mechanics, quantum mechanical system (such as a molecule, an atom or a subatomic particle) transits from an excited state, excited energy state to a lower energy state (e.g., its ground state) and emits a quantized amount of energy in the form of a photon. Spontaneous emission is ultimately responsible for most of the light we see all around us; it is so ubiquitous that there are many names given to what is essentially the same process. If atoms (or molecules) are excited by some means other than heating, the spontaneous emission is called luminescence. For example, fireflies are luminescent. And there are different forms of luminescence depending on how excited atoms are produced (electroluminescence, chemiluminescence etc.). If the excitation is affected by the absorption of radiation the spontaneous emission is called fluorescence. Sometimes molecules have a metastable level and continue to fluoresce long after the exciting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Stress
Shear stress (often denoted by , Greek alphabet, Greek: tau) is the component of stress (physics), stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. ''Normal stress'', on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts. General shear stress The formula to calculate average shear stress or force per unit area is: \tau = ,where is the force applied and is the cross-sectional area. The area involved corresponds to the material face (geometry), face parallel to the applied force vector, i.e., with surface normal vector perpendicular to the force. Other forms Wall shear stress Wall shear stress expresses the retarding force (per unit area) from a wall in the layers of a fluid flowing next to the wall. It is defined as:\tau_w := \mu\left.\frac\_,where is the dynamic viscosity, is the flow velocity, and is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. The proper time interval between two events on a world line is the change in proper time, which is independent of coordinates, and is a Lorentz scalar. The interval is the quantity of interest, since proper time itself is fixed only up to an arbitrary additive constant, namely the setting of the clock at some event along the world line. The proper time interval between two events depends not only on the events, but also the world line connecting them, and hence on the motion of the clock between the events. It is expressed as an integral over the world line (analogous to arc length in Euclidean space). An accelerated clock will measure a smaller elapsed time between two events than that measured by a non-accelerated ( inertial) clock between the same two events. The twin paradox is an example of this effect. By conventio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prouhet–Thue–Morse Constant
In mathematics, the Prouhet–Thue–Morse constant, named for , Axel Thue, and Marston Morse, is the number—denoted by —whose binary expansion 0.01101001100101101001011001101001... is given by the Prouhet–Thue–Morse sequence. That is, : \tau = \sum_^ \frac = 0.412454033640 \ldots where is the element of the Prouhet–Thue–Morse sequence. Other representations The Prouhet–Thue–Morse constant can also be expressed, without using , as an infinite product, : \tau = \frac\left -\prod_^\left(1-\frac\right)\right This formula is obtained by substituting ''x'' = 1/2 into generating series for : F(x) = \sum_^ (-1)^ x^n = \prod_^ ( 1 - x^ ) The continued fraction expansion of the constant is ; 2, 2, 2, 1, 4, 3, 5, 2, 1, 4, 2, 1, 5, 44, 1, 4, 1, 2, 4, 1, … Yann Bugeaud and Martine Queffélec showed that infinitely many partial quotients of this continued fraction are 4 or 5, and infinitely many partial quotients are greater than or equal to 50. Transcendence Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Translation (geometry)
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same Distance geometry, distance in a given direction (geometry), direction. A translation can also be interpreted as the addition of a constant vector space, vector to every point, or as shifting the Origin (mathematics), origin of the coordinate system. In a Euclidean space, any translation is an isometry. As a function If \mathbf is a fixed vector, known as the ''translation vector'', and \mathbf is the initial position of some object, then the translation function T_ will work as T_(\mathbf)=\mathbf+\mathbf. If T is a translation, then the image (mathematics), image of a subset A under the function (mathematics), function T is the translate of A by T . The translate of A by T_ is often written as A+\mathbf . Application in classical physics In classical physics, translational motion is movement that changes the Position (geometry), positio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
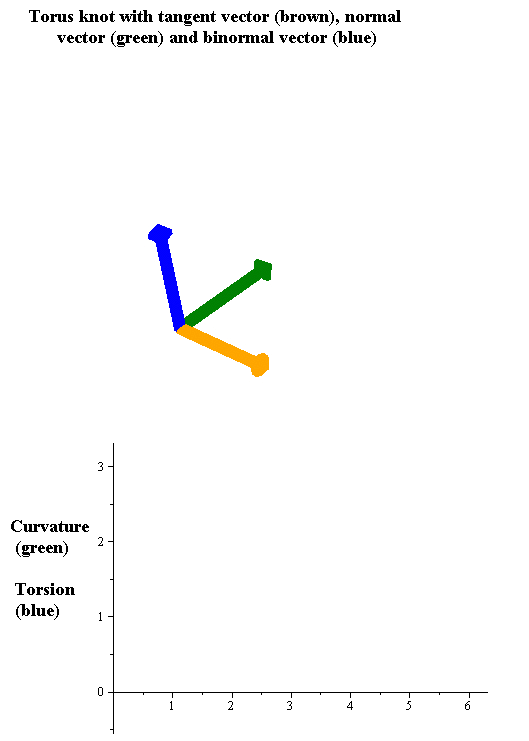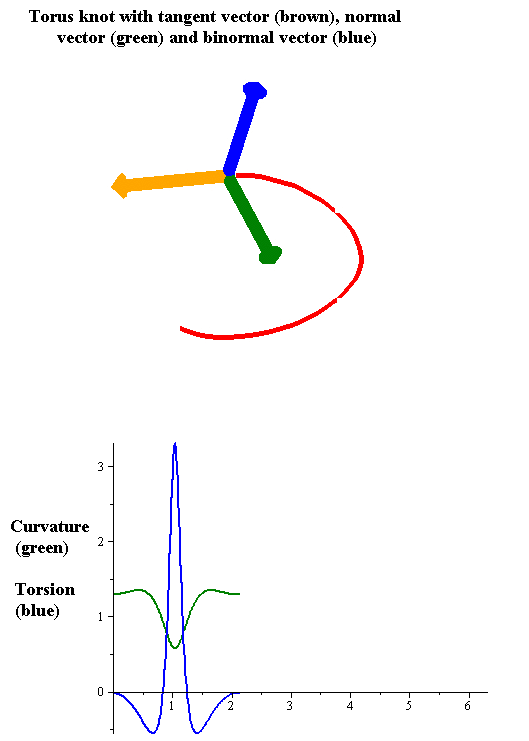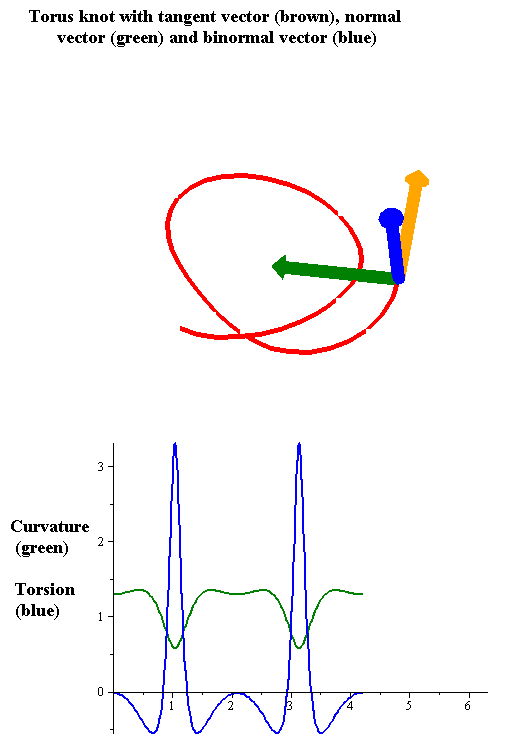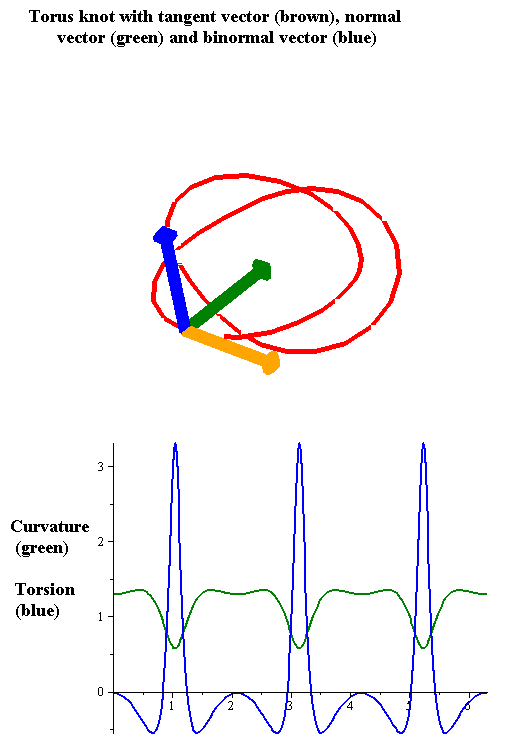
Torsion Of A Curve
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas. Definition Let be a space curve parametrized by arc length and with the unit tangent vector . If the curvature of at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors : \mathbf=\frac, \quad \mathbf=\mathbf\times\mathbf respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation : \mathbf' = -\tau\mathbf. which means : \tau = -\mathbf\cdot\math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tau Function (other) , an arithmetic function giving the number of divisors of an integer
{{disambiguation ...
Tau function may refer to: * Tau function (integrable systems), in integrable systems * Ramanujan tau function, giving the Fourier coefficients of the Ramanujan modular form * Divisor function In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (includi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tau (mathematical Constant)
The number (; spelled out as tau) is a mathematical constant that is the ratio of a circle's circumference to its radius. It is approximately equal to 6.28 and exactly equal to 2Pi, . and are both circle constants relating the circumference of a circle to its linear dimension: the radius in the case of ; the diameter in the case of . While is used almost exclusively in mainstream mathematical education and practice, it has been proposed, most notably by Michael Hartl in 2010, that should be used instead. Hartl and other proponents argue that is the more natural circle constant and its use leads to conceptually simpler and more intuitive mathematical notation. Critics have responded that the benefits of using over are trivial and that given the ubiquity and historical significance of a change is unlikely to occur. The proposal did not initially gain widespread acceptance in the mathematical community, but awareness of has become more widespread, having been added to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stopping Time
In probability theory, in particular in the study of stochastic processes, a stopping time (also Markov time, Markov moment, optional stopping time or optional time ) is a specific type of "random time": a random variable whose value is interpreted as the time at which a given stochastic process exhibits a certain behavior of interest. A stopping time is often defined by a stopping rule, a mechanism for deciding whether to continue or stop a process on the basis of the present position and past events, and which will almost always lead to a decision to stop at some finite time. Stopping times occur in decision theory, and the optional stopping theorem is an important result in this context. Stopping times are also frequently applied in mathematical proofs to "tame the continuum of time", as Chung put it in his book (1982). Definition Discrete time Let \tau be a random variable, which is defined on the filtered probability space (\Omega, \mathcal F, (\mathcal F_n)_, P) w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kendall Tau Rank Correlation Coefficient
In statistics, the Kendall rank correlation coefficient, commonly referred to as Kendall's τ coefficient (after the Greek letter τ, tau), is a statistic used to measure the ordinal association between two measured quantities. A τ test is a non-parametric hypothesis test for statistical dependence based on the τ coefficient. It is a measure of rank correlation: the similarity of the orderings of the data when ranked by each of the quantities. It is named after Maurice Kendall, who developed it in 1938, though Gustav Fechner had proposed a similar measure in the context of time series in 1897. Intuitively, the Kendall correlation between two variables will be high when observations have a similar (or identical for a correlation of 1) rank (i.e. relative position label of the observations within the variable: 1st, 2nd, 3rd, etc.) between the two variables, and low when observations have a dissimilar (or fully different for a correlation of −1) rank between the two variab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |