|
Sum Of Normally Distributed Random Variables
In probability theory, calculation of the sum of normally distributed random variables is an instance of the arithmetic of random variables, which can be quite complex based on the probability distributions of the random variables involved and their relationships. This is not to be confused with the sum of normal distributions which forms a mixture distribution. Independent random variables Let ''X'' and ''Y'' be independent random variables that are normally distributed (and therefore also jointly so), then their sum is also normally distributed. i.e., if :X \sim N(\mu_X, \sigma_X^2) :Y \sim N(\mu_Y, \sigma_Y^2) :Z=X+Y, then :Z \sim N(\mu_X + \mu_Y, \sigma_X^2 + \sigma_Y^2). This means that the sum of two independent normally distributed random variables is normal, with its mean being the sum of the two means, and its variance being the sum of the two variances (i.e., the square of the standard deviation is the sum of the squares of the standard deviations). In order for thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slash Distribution
In probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate. In other words, if the random variable ''Z'' has a normal distribution with zero mean and unit variance, the random variable ''U'' has a uniform distribution on ,1and ''Z'' and ''U'' are statistically independent, then the random variable ''X'' = ''Z'' / ''U'' has a slash distribution. The slash distribution is an example of a ratio distribution. The distribution was named by William H. Rogers and John Tukey in a paper published in 1972. The probability density function (pdf) is : f(x) = \frac. where \varphi(x) is the probability density function of the standard normal distribution. The quotient is undefined at ''x'' = 0, but the discontinuity is removable: : \lim_ f(x) = \frac = \frac The most common use of the slash distribution is in simulation studies. It is a useful distribution in this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Distribution
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables ''X'' and ''Y'', the distribution of the random variable ''Z'' that is formed as the product Z = XY is a ''product distribution''. Algebra of random variables The product is one type of algebra for random variables: Related to the product distribution are the ratio distribution, sum distribution (see List of convolutions of probability distributions) and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios. Many of these distributions are described in Melvin D. Springer's book from 1979 ''The Algebra of Random Variables''. Derivation for independent random variables If X and Y are two independent, continuous random variables, described by probability density functions f_X and f_Y then the probability densi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
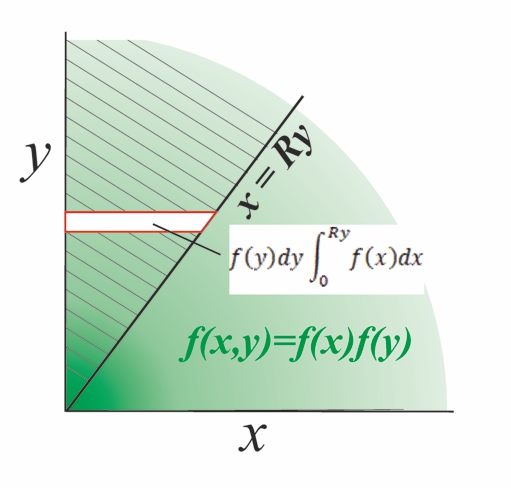
Ratio Distribution
A ratio distribution (also known as a quotient distribution) is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two (usually independent) random variables ''X'' and ''Y'', the distribution of the random variable ''Z'' that is formed as the ratio ''Z'' = ''X''/''Y'' is a ''ratio distribution''. An example is the Cauchy distribution (also called the ''normal ratio distribution''), which comes about as the ratio of two normally distributed variables with zero mean. Two other distributions often used in test-statistics are also ratio distributions: the ''t''-distribution arises from a Gaussian random variable divided by an independent chi-distributed random variable, while the ''F''-distribution originates from the ratio of two independent chi-squared distributed random variables. More general ratio distributions have been considered in the literature. Often the ratio distributions are heavy- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Error (statistics)
The standard error (SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM). The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean. Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Distribution
In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.B. Mandelbrot, The Pareto–Lévy Law and the Distribution of Income, International Economic Review 1960 https://www.jstor.org/stable/2525289 Of the four parameters defining the family, most attention has been focused on the stability parameter, \alpha (see panel). Stable distributions have 0 < \alpha \leq 2, with the upper bound corresponding to the , and to the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Of Random Variables
The algebra of random variables in statistics, provides rules for the symbolic manipulation of random variables, while avoiding delving too deeply into the mathematically sophisticated ideas of probability theory. Its symbolism allows the treatment of sums, products, ratios and general functions of random variables, as well as dealing with operations such as finding the probability distributions and the expectations (or expected values), variances and covariances of such combinations. In principle, the elementary algebra of random variables is equivalent to that of conventional non-random (or deterministic) variables. However, the changes occurring on the probability distribution of a random variable obtained after performing algebraic operations are not straightforward. Therefore, the behavior of the different operators of the probability distribution, such as expected values, variances, covariances, and moments, may be different from that observed for the random variable u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propagation Of Uncertainty
In statistics, propagation of uncertainty (or propagation of error) is the effect of variables' uncertainties (or errors, more specifically random errors) on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations (e.g., instrument precision) which propagate due to the combination of variables in the function. The uncertainty ''u'' can be expressed in a number of ways. It may be defined by the absolute error . Uncertainties can also be defined by the relative error , which is usually written as a percentage. Most commonly, the uncertainty on a quantity is quantified in terms of the standard deviation, , which is the positive square root of the variance. The value of a quantity and its error are then expressed as an interval . If the statistical probability distribution of the variable is known or can be assumed, it is possible to derive confidence limits to describe th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance Matrix
In probability theory and statistics, a covariance matrix (also known as auto-covariance matrix, dispersion matrix, variance matrix, or variance–covariance matrix) is a square matrix giving the covariance between each pair of elements of a given random vector. Any covariance matrix is symmetric and positive semi-definite and its main diagonal contains variances (i.e., the covariance of each element with itself). Intuitively, the covariance matrix generalizes the notion of variance to multiple dimensions. As an example, the variation in a collection of random points in two-dimensional space cannot be characterized fully by a single number, nor would the variances in the x and y directions contain all of the necessary information; a 2 \times 2 matrix would be necessary to fully characterize the two-dimensional variation. The covariance matrix of a random vector \mathbf is typically denoted by \operatorname_ or \Sigma. Definition Throughout this article, boldfaced unsub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. Howev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |