|
Covariance Matrix
In probability theory and statistics, a covariance matrix (also known as auto-covariance matrix, dispersion matrix, variance matrix, or variance–covariance matrix) is a square matrix giving the covariance between each pair of elements of a given random vector. Any covariance matrix is symmetric and positive semi-definite and its main diagonal contains variances (i.e., the covariance of each element with itself). Intuitively, the covariance matrix generalizes the notion of variance to multiple dimensions. As an example, the variation in a collection of random points in two-dimensional space cannot be characterized fully by a single number, nor would the variances in the x and y directions contain all of the necessary information; a 2 \times 2 matrix would be necessary to fully characterize the two-dimensional variation. The covariance matrix of a random vector \mathbf is typically denoted by \operatorname_ or \Sigma. Definition Throughout this article, boldfaced unsub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonal Matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is \left begin 3 & 0 \\ 0 & 2 \end\right/math>, while an example of a 3×3 diagonal matrix is \left begin 6 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end\right/math>. An identity matrix of any size, or any multiple of it (a scalar matrix), is a diagonal matrix. A diagonal matrix is sometimes called a scaling matrix, since matrix multiplication with it results in changing scale (size). Its determinant is the product of its diagonal values. Definition As stated above, a diagonal matrix is a matrix in which all off-diagonal entries are zero. That is, the matrix with ''n'' columns and ''n'' rows is diagonal if \forall i,j \in \, i \ne j \implies d_ = 0. However, the main diagonal entries are unrestricted. The term ''diagonal matrix'' may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
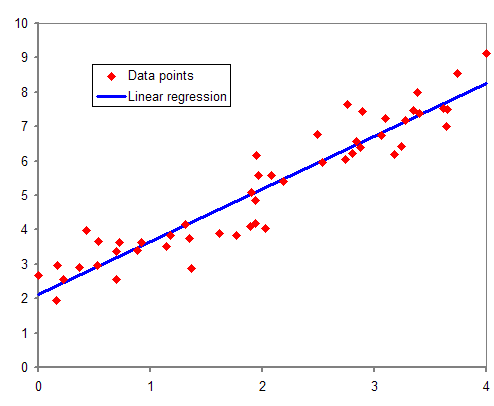
Normal Equations
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown statistical parameter, parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting Statistical estimation, estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regressi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schur Complement
In linear algebra and the theory of matrices, the Schur complement of a block matrix is defined as follows. Suppose ''p'', ''q'' are nonnegative integers, and suppose ''A'', ''B'', ''C'', ''D'' are respectively ''p'' × ''p'', ''p'' × ''q'', ''q'' × ''p'', and ''q'' × ''q'' matrices of complex numbers. Let :M = \left begin A & B \\ C & D \end\right/math> so that ''M'' is a (''p'' + ''q'') × (''p'' + ''q'') matrix. If ''D'' is invertible, then the Schur complement of the block ''D'' of the matrix ''M'' is the ''p'' × ''p'' matrix defined by :M/D := A - BD^C. If ''A'' is invertible, the Schur complement of the block ''A'' of the matrix ''M'' is the ''q'' × ''q'' matrix defined by :M/A := D - CA^B. In the case that ''A'' or ''D'' is singular, substituting a generalized inverse for the inverses on ''M/A'' and ''M/D'' yields the generalized Schur complement. The Schur complement is named after Issai Schur who used it to prove Schur's lemma, although it had been used previous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a give ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Variance
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models. Definition The conditional variance of a random variable ''Y'' given another random variable ''X'' is :\operatorname(Y, X) = \operatorname\Big(\big(Y - \operatorname(Y\mid X)\big)^\mid X\Big). The conditional variance tells us how much variance is left if we use \operatorname(Y\mid X) to "predict" ''Y''. Here, as usual, \operatorname(Y\mid X) stands for the conditional expectation of ''Y'' given ''X'', which we may recall, is a random variable itself (a function of ''X'', determined up to probability one). As a result, \operatorname(Y, X) itself is a random variable (and is a function of ''X''). Explanation, r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Mean
In probability theory, the conditional expectation, conditional expected value, or conditional mean of a random variable is its expected value – the value it would take “on average” over an arbitrarily large number of occurrences – given that a certain set of "conditions" is known to occur. If the random variable can take on only a finite number of values, the “conditions” are that the variable can only take on a subset of those values. More formally, in the case when the random variable is defined over a discrete probability space, the "conditions" are a partition of this probability space. Depending on the context, the conditional expectation can be either a random variable or a function. The random variable is denoted E(X\mid Y) analogously to conditional probability. The function form is either denoted E(X\mid Y=y) or a separate function symbol such as f(y) is introduced with the meaning E(X\mid Y) = f(Y). Examples Example 1: Dice rolling Consider the roll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Distribution
In probability theory and statistics, given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value x of X as a parameter. When both X and Y are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable. If the conditional distribution of Y given X is a continuous distribution, then its probability density function is known as the conditional density function. The properties of a conditional distribution, such as the moments, are often referred to by corresponding names such as the conditional mean and conditional variance. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marginal Distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the subset without reference to the values of the other variables. This contrasts with a conditional distribution, which gives the probabilities contingent upon the values of the other variables. Marginal variables are those variables in the subset of variables being retained. These concepts are "marginal" because they can be found by summing values in a table along rows or columns, and writing the sum in the margins of the table. The distribution of the marginal variables (the marginal distribution) is obtained by marginalizing (that is, focusing on the sums in the margin) over the distribution of the variables being discarded, and the discarded variables are said to have been marginalized out. The context here is that the theore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-semidefinite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z^* Mz is positive for every nonzero complex column vector z, where z^* denotes the conjugate transpose of z. Positive semi-definite matrices are defined similarly, except that the scalars z^\textsfMz and z^* Mz are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called indefinite. A matrix is thus positive-definite if and only if it is the matrix of a positive-definite quadratic form or Hermitian form. In other words, a matrix is positive-definite if and only if it defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Correlation
In probability theory and statistics, partial correlation measures the degree of association between two random variables, with the effect of a set of controlling random variables removed. When determining the numerical relationship between two variables of interest, using their correlation coefficient will give misleading results if there is another confounding variable that is numerically related to both variables of interest. This misleading information can be avoided by controlling for the confounding variable, which is done by computing the partial correlation coefficient. This is precisely the motivation for including other right-side variables in a multiple regression; but while multiple regression gives unbiased results for the effect size, it does not give a numerical value of a measure of the strength of the relationship between the two variables of interest. For example, given economic data on the consumption, income, and wealth of various individuals, consider the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |