|
Structure Of Liquids And Glasses
The structure of liquids, glasses and other non-crystalline solids is characterized by the absence of long-range order which defines crystalline materials. Liquids and amorphous solids do, however, possess a rich and varied array of short to medium range order, which originates from chemical bonding and related interactions. Metallic glasses, for example, are typically well described by the dense random packing of hard spheres, whereas covalent systems, such as silicate glasses, have sparsely packed, strongly bound, tetrahedral network structures. These very different structures result in materials with very different physical properties and applications. The study of liquid and glass structure aims to gain insight into their behavior and physical properties, so that they can be understood, predicted and tailored for specific applications. Since the structure and resulting behavior of liquids and glasses is a complex many body problem, historically it has been too computation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liquid
Liquid is a state of matter with a definite volume but no fixed shape. Liquids adapt to the shape of their container and are nearly incompressible, maintaining their volume even under pressure. The density of a liquid is usually close to that of a solid, and much higher than that of a gas. Therefore, liquid and solid are classified as condensed matter. Meanwhile, since both liquids and gases can flow, they are categorized as fluids. A liquid is composed of atoms or molecules held together by intermolecular bonds of intermediate strength. These forces allow the particles to move around one another while remaining closely packed. In contrast, solids have particles that are tightly bound by strong intermolecular forces, limiting their movement to small vibrations in fixed positions. Gases, on the other hand, consist of widely spaced, freely moving particles with only weak intermolecular forces. As temperature increases, the molecules in a liquid vibrate more intensely, causi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pair Distribution Function
The pair distribution function describes the distribution of distances between pairs of particles contained within a given volume. Mathematically, if ''a'' and ''b'' are two particles, the pair distribution function of ''b'' with respect to ''a'', denoted by g_(\vec) is the probability of finding the particle ''b'' at distance \vec from ''a'', with ''a'' taken as the origin of coordinates. Overview The pair distribution function is used to describe the distribution of objects within a medium (for example, oranges in a crate or nitrogen molecules in a gas cylinder). If the medium is homogeneous (i.e. every spatial location has identical properties), then there is an equal probability density for finding an object at any position \vec: :p(\vec)=1/V, where V is the volume of the container. On the other hand, the likelihood of finding ''pairs of objects'' at given positions (i.e. the two-body probability density) is not uniform. For example, pairs of hard balls must be separated by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pair Correlations
Pair or PAIR or Pairing may refer to: Government and politics * Pair (parliamentary convention), matching of members unable to attend, so as not to change the voting margin * ''Pair'', a member of the Prussian House of Lords * ''Pair'', the French equivalent of peer, holder of a French Pairie, a French high title roughly equivalent to a member of the British peerage Mathematics * 2 (number), two of something, a pair * Unordered pair, or pair set, in mathematics and set theory * Ordered pair, or 2-tuple, in mathematics and set theory * Pairing, in mathematics, an R-bilinear map of modules, where R is the underlying ring * Pair type, in programming languages and type theory, a product type with two component types * Topological pair, an inclusion of topological spaces Science and technology * Couple (app), formerly Pair, a mobile application for two people * PAIR (puncture-aspiration-injection-reaspiration), in medicine * Pairing, a handshaking process in Bluetooth communications ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Distribution Function
In statistical mechanics, the radial distribution function, (or pair correlation function) g(r) in a system of particles (atoms, molecules, colloids, etc.), describes how density varies as a function of distance from a reference particle. If a given particle is taken to be at the origin ''O'', and if \rho = N/V is the average number density of particles, then the local time-averaged density at a distance r from ''O'' is \rho g(r). This simplified definition holds for a homogeneous and isotropic system. A more general case will be considered below. In simplest terms it is a measure of the probability of finding a particle at a distance of r away from a given reference particle, relative to that for an ideal gas. The general algorithm involves determining how many particles are within a distance of r and r+dr away from a particle. This general theme is depicted to the right, where the red particle is our reference particle, and the blue particles are those whose centers are with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of Neutron temperature, thermal or cold neutron radiation, neutrons to obtain a diffraction pattern that provides information of the structure of the material. The technique is similar to X-ray diffraction but due to their different scattering properties, neutrons and X-rays provide complementary information: X-Rays are suited for superficial analysis, strong x-rays from synchrotron radiation are suited for shallow depths or thin specimens, while neutrons having high penetration depth are suited for bulk samples.Measurement of residual stress in materials using neutrons IAEA, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
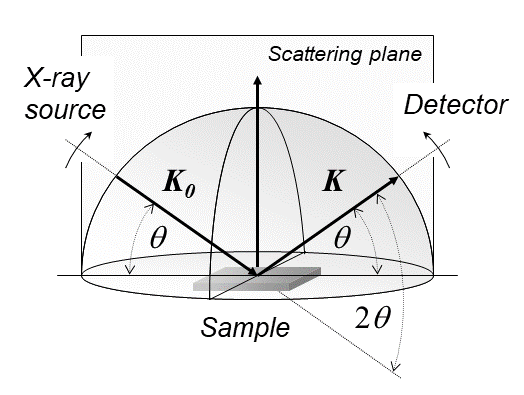
X-ray Diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. The resulting map of the directions of the X-rays far from the sample is called a diffraction pattern. It is different from X-ray crystallography which exploits X-ray diffraction to determine the arrangement of atoms in materials, and also has other components such as ways to map from experimental diffraction measurements to the positions of atoms. This article provides an overview of X-ray diffraction, starting with the early #History, history of x-rays and the discovery that they have the right spacings to be diffracted by crystals. In many cases these diffraction patterns can be #Introduction to x-ray diffraction theory, Interpreted using a single scattering or kinematical theory with conservation of energy (#Ewald's sphere, wave vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bragg Peak
The Bragg peak is a pronounced peak on the Bragg curve which plots the energy loss of ionizing radiation during its travel through matter. For protons, α-rays, and other ion rays, the peak occurs immediately before the particles come to rest. It is named after William Henry Bragg, who discovered it in 1903 using alpha particles from radium, and wrote the first empirical formula for ionization energy loss per distance with Richard Kleeman. When a fast charged particle moves through matter, it ionizes atoms of the material and deposits a dose along its path. A peak occurs because the interaction cross section increases as the charged particle's energy decreases. Energy lost by charged particles is inversely proportional to the square of their velocity, which explains the peak occurring just before the particle comes to a complete stop. In the upper figure, it is the peak for alpha particles of 5.49 MeV moving through air. In the lower figure, it is the narrow peak of the "nat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long-range Order
In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system. In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transitions into less ordered states. Examples for such an order-disorder transition are: * the melting of ice: solid–liquid transition, loss of crystalline order; * the demagnetization of iron by heating above the Curie temperature: ferromagnetic– paramagnetic transition, loss of magnetic order. The degree of freedom that is ordered or disordered can be translational (crystalline ordering), rotational ( ferroelectric ordering), or a spin state ( magnetic ordering). The order can consist either in a full crystalline space group symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of long range order or short range order. If a disordered state is not in thermodynamic e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angstrom
The angstrom (; ) is a unit of length equal to m; that is, one ten-billionth of a metre, a hundred-millionth of a centimetre, 0.1 nanometre, or 100 picometres. The unit is named after the Swedish physicist Anders Jonas Ångström (1814–1874). It was originally spelled with Swedish letters, as Ångström and later as ångström (). The latter spelling is still listed in some dictionaries, but is now rare in English texts. Some popular US dictionaries list only the spelling ''angstrom''. The unit's symbol is Å, which is a letter of the Swedish alphabet, regardless of how the unit is spelled. However, "A" or "A.U." may be used in less formal contexts or typographically limited media. The angstrom is often used in the natural sciences and technology to express sizes of atoms, molecules, microscopic biological structures, and lengths of chemical bonds, arrangement of atoms in crystals, wavelengths of electromagnetic radiation, and dimensions of integrated circuit part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Angle Scattering
Small-angle scattering (SAS) is a scattering technique based on deflection of collimated radiation away from the straight trajectory after it interacts with structures that are much larger than the wavelength of the radiation. The deflection (physics), deflection is small (0.1-10°) hence the name ''small-angle''. SAS techniques can give information about the size, shape and orientation of structures in a sample. SAS is a powerful technique for investigating large-scale structures from 10 Ångström, Å up to thousands and even several tens of thousands of Ångström, angstroms. The most important feature of the SAS method is its potential for analyzing the inner structure of disordered systems, and frequently the application of this method is a unique way to obtain direct structural information on systems with random arrangement of density inhomogeneities in such large-scales. Currently, the SAS technique, with its well-developed experimental and theoretical procedures and wide r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |