|
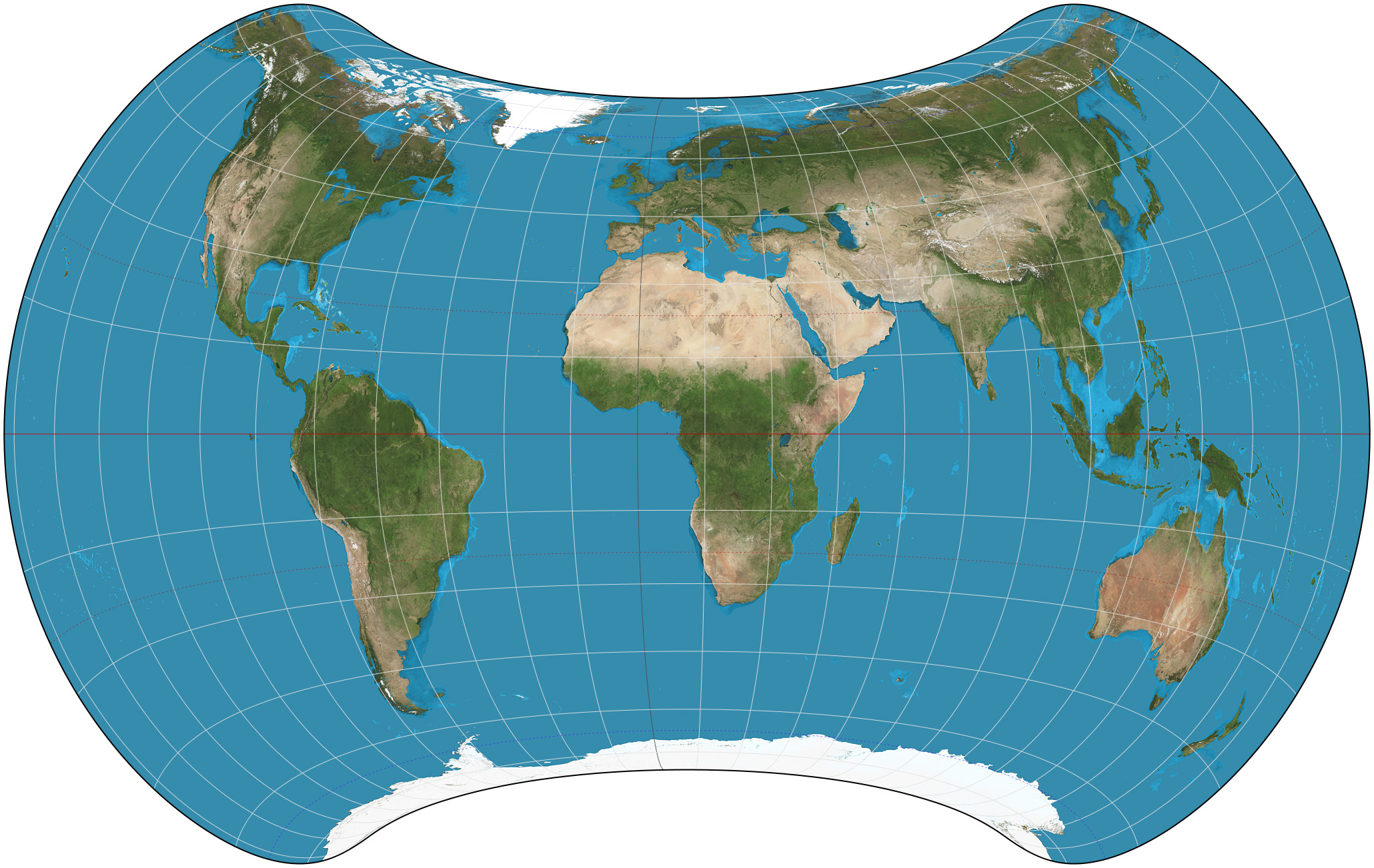
Strebe 1995 Projection
The Strebe 1995 projection, Strebe projection, Strebe lenticular equal-area projection, or Strebe equal-area polyconic projection is an equal-area map projection presented by Daniel "daan" Strebe in 1994. Strebe designed the projection to keep all areas proportionally correct in size; to push as much of the inevitable distortion as feasible away from the continental masses and into the Pacific Ocean; to keep a familiar equatorial orientation; and to do all this without slicing up the map. Description Strebe first presented the projection at a joint meeting of the Canadian Cartographic Association and the North American Cartographic Information Society (NACIS) in August 1994. Its final formulation was completed in 1995. The projection has been available in the map projection software Geocart since Geocart 1.2, released in October 1994. The projection is arrived at by a series of steps, each of which preserves areas. Because each step preserves areas, the entire process preserv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal-area Projection
In cartography, an equivalent, authalic, or equal-area projection is a map projection that preserves relative area measure between any and all map regions. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, and so forth, because an equal-area map does not change apparent density of the phenomenon being mapped. By Carl Friedrich Gauss, Gauss's Theorema Egregium, an equal-area projection cannot be conformal map projection, conformal. This implies that an equal-area projection inevitably distorts shapes. Even though a point or points or a path or paths on a map might have no distortion, the greater the area of the region being mapped, the greater and more obvious the distortion of shapes inevitably becomes. Description In order for a map projection of the sphere to be equal-area, its generating formulae must meet this Cauchy-Riemann equations, Cauchy-Riemann-like condition: :\frac \cdo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
North American Cartographic Information Society
The North American Cartographic Information Society (NACIS) is a US-based cartographic society founded in 1980. It was founded by specialists in cartography, which included government mapmakers, map librarians, cartography professors and cartography lab directors. It now represents a broad mixture of academic, government and commercial interests, with a sizeable proportion of working cartographers. Many NACIS members come from related vocations (e.g. art, design, information visualization, GIS, historical research, and software development.) NACIS offers both volunteer opportunities and travel grants for students and members of the community. Objectives To improve communication, coordination and cooperation among the producers, disseminators, curators, and users of cartographic information. To support and coordinate activities with other professional organizations and institutions involved with cartographic information. To improve the use of cartographic materials through educati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckert IV Projection
The Eckert IV projection is an equal-area pseudocylindrical map projection. The length of the polar lines is half that of the equator, and lines of longitude are semiellipses, or portions of ellipses. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, meridians are the same whereas parallels differ. Odd-numbered projections have parallels spaced equally, whereas even-numbered projections have parallels spaced to preserve area. Eckert IV is paired with Eckert III. Formulas Forward formulae Given a sphere of radius ''R'', central meridian ''λ'' and a point with geographical latitude ''φ'' and longitude ''λ'', plane coordinates ''x'' and ''y'' can be computed using the following formulas: : \begin x & = \frac R\, (\lambda - \lambda_0)(1 + \cos \theta) \approx 0.422\,2382\, R\, (\lambda - \lambda_0)(1 + \cos \theta), \\ pty & = 2 \sqrt R \sin \theta \approx 1.326\,5004\, R \sin \theta, \end where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mollweide Projection
400px, Mollweide projection of the world 400px, The Mollweide projection with Tissot's indicatrix of deformation The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions. The projection was first published by mathematician and astronomer Karl (or Carl) Brandan Mollweide (1774–1825) of Leipzig in 1805. It was reinvented and popularized in 1857 by Jacques Babinet, who gave it the name homalographic projection. The variation homolographic arose from frequent nineteenth-century usage in star atlases. Properties The Mollweide is a pseudocylindrical projection in which the equator is represented as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hammer Projection
The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide. Development Directly inspired by the Aitoff projection, Hammer suggested the use of the equatorial form of the Lambert azimuthal equal-area projection instead of Aitoff's use of the azimuthal equidistant projection: :\begin x &= \operatorname_x\left(\frac, \varphi\right) \\ y &= \tfrac12 \operatorname_y\left(\frac, \varphi\right) \end where laea and laea are the ''x'' and ''y'' components of the equatorial Lambert azimuthal equal-area projection. Written out explicitly: :\begin x &= \frac \\ y &= \frac \end The inverse is calculated with the intermediate variable :z \equiv \sqrt The longitude and latitudes can then be calculated by :\begin \lambda &= 2 \arctan \frac \\ \varphi &= \arcsin zy \end where ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chukchi Peninsula
The Chukchi Peninsula (also Chukotka Peninsula or Chukotski Peninsula; , ''Chukotskiy poluostrov'', short form , ''Chukotka''), at about 66° N 172° W, is the easternmost peninsula of Asia. Its eastern end is at Cape Dezhnev near the village of Uelen. The Chukotka Mountains are located in the central/western part of the peninsula, which is bounded by the Chukchi Sea to the north, the Bering Sea to the south, and the Bering Strait to the east, where at its easternmost point it is only about from Seward Peninsula in Alaska; this is the smallest distance between the land masses of Eurasia and North America. The peninsula is part of Chukotka Autonomous Okrug of Russia. Accessed September 2010. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |