|
Strategic Complements
In economics and game theory, the decisions of two or more players are called strategic complements if they mutually reinforce one another, and they are called strategic substitutes if they mutually offset one another. These terms were originally coined by Bulow, Geanakoplos, and Klemperer (1985). To see what is meant by 'reinforce' or 'offset', consider a situation in which the players all have similar choices to make, as in the paper of Bulow et al., where the players are all imperfectly competitive firms that must each decide how much to produce. Then the production decisions are strategic complements if an increase in the production of one firm increases the marginal revenues of the others, because that gives the others an incentive to produce more too. This tends to be the case if there are sufficiently strong aggregate increasing returns to scale and/or the demand curves for the firms' products have a sufficiently low own-price elasticity. On the other hand, the production d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyses what is viewed as basic elements within economy, economies, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyses economies as systems where production, distribution, consumption, savings, and Expenditure, investment expenditure interact; and the factors of production affecting them, such as: Labour (human activity), labour, Capital (economics), capital, Land (economics), land, and Entrepreneurship, enterprise, inflation, economic growth, and public policies that impact gloss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave Function
In mathematics, a concave function is one for which the function value at any convex combination of elements in the domain is greater than or equal to that convex combination of those domain elements. Equivalently, a concave function is any function for which the hypograph is convex. The class of concave functions is in a sense the opposite of the class of convex functions. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex. Definition A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be ''concave'' if, for any x and y in the interval and for any \alpha \in ,1/math>, :f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y) A function is called ''strictly concave'' if :f((1-\alpha )x+\alpha y) > (1-\alpha ) f(x)+\alpha f(y) for any \alpha \in (0,1) and x \neq y. For a function f: \mathbb \to \mathbb, this second definition merely states that for ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplier (economics)
In macroeconomics, a multiplier is a factor of proportionality that measures how much an endogenous variable changes in response to a change in some exogenous variable. For example, suppose variable ''x'' changes by ''k'' units, which causes another variable ''y'' to change by ''M'' × ''k'' units. Then the multiplier is ''M''. Common uses Two multipliers are commonly discussed in introductory macroeconomics. Commercial banks create money, especially under the fractional-reserve banking system used throughout the world. In this system, money is created whenever a bank gives out a new loan. This is because the loan, when drawn on and spent, mostly finishes up as a deposit back in the banking system and is counted as part of money supply. After putting aside a part of these deposits as mandated bank reserves, the balance is available for the making of further loans by the bank. This process continues multiple times, and is called the multiplier effect. The multiplier m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Failure (economics)
In economics, coordination failure is a concept that can explain recessions through the failure of firms and other price setters to coordinate. In an economic system with multiple equilibria, coordination failure occurs when a group of firms could achieve a more desirable equilibrium but fail to because they do not coordinate their decision making. Coordination failure can result in a self-fulfilling prophecy.Romer, 305. For example, if one firm decides a recession is imminent and fires its workers, other firms might lose demand from the lay-offs and respond by firing their own workers leading to a recession at a new equilibrium. Coordination failure can also be associated with sunspot equilibria (where equilibria are the result of variables that do not have any real impact on fundamentals) and animal spirits. Coordination failure can lead to an underemployment equilibrium. Coordination failure also implies that fiscal policy can mitigate the effects of recessions, or eve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
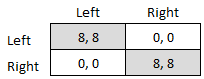
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibrium, Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supermodular
In mathematics, a supermodular function is a function on a lattice that, informally, has the property of being characterized by "increasing differences." Seen from the point of set functions, this can also be viewed as a relationship of "increasing returns", where adding more elements to a subset increases its valuation. In economics, supermodular functions are often used as a formal expression of complementarity in preferences among goods. Supermodular functions are studied and have applications in game theory, economics, lattice theory, combinatorial optimization, and machine learning. Definition Let (X, \preceq) be a lattice. A real-valued function f: X \rightarrow \mathbb is called supermodular if f(x \vee y) + f(x \wedge y) \geq f(x) + f(y) for all x, y \in X. If the inequality is strict, then f is strictly supermodular on X. If -f is (strictly) supermodular then ''f'' is called (strictly) submodular. A function that is both submodular and supermodular is called modula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Submodular Set Function
In mathematics, a submodular set function (also known as a submodular function) is a set function that, informally, describes the relationship between a set of inputs and an output, where adding more of one input has a decreasing additional benefit ( diminishing returns). The natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory (as functions modeling user preferences) and electrical networks. Recently, submodular functions have also found utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains. Definition If \Omega is a finite set, a submodular function is a set function f:2^\rightarrow \mathbb, where 2^\Omega denotes the power set of \Omega, which satisfies one of the following equivalent condit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supermodular
In mathematics, a supermodular function is a function on a lattice that, informally, has the property of being characterized by "increasing differences." Seen from the point of set functions, this can also be viewed as a relationship of "increasing returns", where adding more elements to a subset increases its valuation. In economics, supermodular functions are often used as a formal expression of complementarity in preferences among goods. Supermodular functions are studied and have applications in game theory, economics, lattice theory, combinatorial optimization, and machine learning. Definition Let (X, \preceq) be a lattice. A real-valued function f: X \rightarrow \mathbb is called supermodular if f(x \vee y) + f(x \wedge y) \geq f(x) + f(y) for all x, y \in X. If the inequality is strict, then f is strictly supermodular on X. If -f is (strictly) supermodular then ''f'' is called (strictly) submodular. A function that is both submodular and supermodular is called modula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Game
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. Symmetry can come in different varieties. Ordinally symmetric games are games that are symmetric with respect to the ordinal structure of the payoffs. A game is quantitatively symmetric if and only if it is symmetric with respect to the exact payoffs. A partnership game is a symmetric game where both players receive identical payoffs for any strategy set. That is, the payoff for playing strategy ''a'' against strategy ''b'' receives the same payoff as playing strategy ''b'' against strategy ''a''. Symmetry in 2x2 games Only 12 out of the 144 ordinally distinct 2x2 games are symmetric. However, many of the commonly studied 2x2 games are at least ordinally symmetric. The standard represe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibrium, Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Equilibrium
In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an overall general equilibrium. General equilibrium theory contrasts with the theory of ''partial'' equilibrium, which analyzes a specific part of an economy while its other factors are held constant. General equilibrium theory both studies economies using the model of equilibrium pricing and seeks to determine in which circumstances the assumptions of general equilibrium will hold. The theory dates to the 1870s, particularly the work of French economist Léon Walras in his pioneering 1874 work ''Elements of Pure Economics''. The theory reached its modern form with the work of Lionel W. McKenzie (Walrasian theory), Kenneth Arrow and Gérard Debreu (Hicksian theory) in the 1950s. Overview Broadly speaking, general equilibrium tries to give a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |