|
Slope (geometry)
In mathematics, the slope or gradient of a line is a number that describes the direction of the line on a plane. Often denoted by the letter ''m'', slope is calculated as the ratio of the vertical change to the horizontal change ("rise over run") between two distinct points on the line, giving the same number for any choice of points. The line may be physical – as set by a road surveyor, pictorial as in a diagram of a road or roof, or abstract. An application of the mathematical concept is found in the grade or gradient in geography and civil engineering. The ''steepness'', incline, or grade of a line is the absolute value of its slope: greater absolute value indicates a steeper line. The line trend is defined as follows: *An "increasing" or "ascending" line goes from left to right and has positive slope: m>0. *A "decreasing" or "descending" line goes from left to right and has negative slope: m<0. Special directions are: *A "(square) |
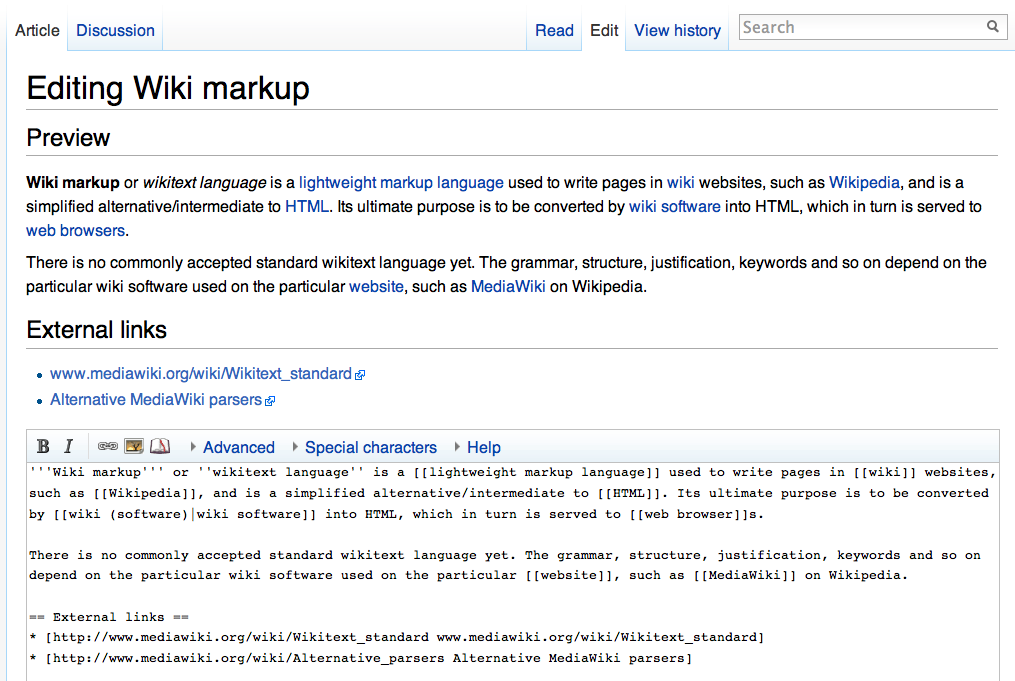
Wiki Slope In 2d
A wiki ( ) is a form of hypertext publication on the internet which is collaboratively edited and managed by its audience directly through a web browser. A typical wiki contains multiple pages that can either be edited by the public or limited to use within an organization for maintaining its internal knowledge base. Its name derives from the first user-editable website called "WikiWikiWeb," with "wiki" being a Hawaiian word meaning "quick." Wikis are powered by wiki software, also known as wiki engines. Being a form of content management system, these differ from other web-based systems such as blog software or static site generators in that the content is created without any defined owner or leader. Wikis have little inherent structure, allowing one to emerge according to the needs of the users. Wiki engines usually allow content to be written using a lightweight markup language and sometimes edited with the help of a rich-text editor. There are dozens of different wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta (letter)
Delta ( ; uppercase Δ, lowercase δ; , ''délta'', ) is the fourth letter of the Greek alphabet. In the system of Greek numerals, it has a value of four. It was derived from the Phoenician alphabet, Phoenician letter Dalet (letter), dalet 𐤃. Letters that come from delta include the Latin alphabet, Latin D and the Cyrillic script, Cyrillic De (Cyrillic), Д. A river delta (originally, the Nile Delta, delta of the Nile River) is named so because its shape approximates the triangular uppercase letter delta. Contrary to a popular legend, this use of the word ''delta'' was not coined by Herodotus. Pronunciation In Ancient Greek, delta represented a voiced dental plosive . In Modern Greek, it represents a voiced dental fricative , like the "''th''" in "''that''" or "''this''" (while in foreign words is instead commonly transcribed as ντ). Delta is romanization of Greek, romanized as ''d'' or ''dh''. Uppercase The uppercase letter Δ is used to denote: * Change of any changeable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Of A Line In Coordinates From -12x+2 To +12x+2
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
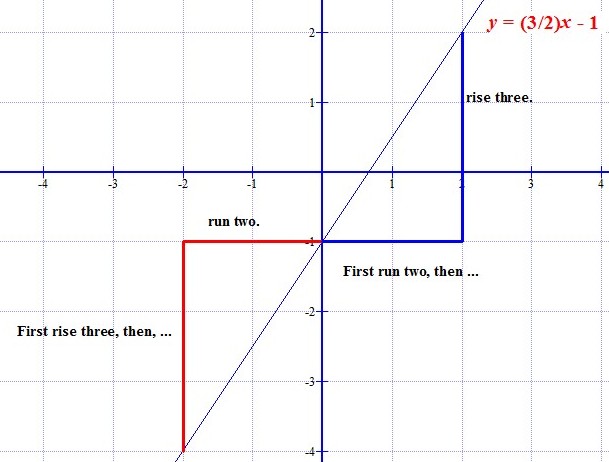
Slope Of Lines Illustrated
In mathematics, the slope or gradient of a Line (mathematics), line is a number that describes the direction (geometry), direction of the line on a plane (geometry), plane. Often denoted by the letter ''m'', slope is calculated as the ratio of the vertical change to the horizontal change ("rise over run") between two distinct points on the line, giving the same number for any choice of points. The line may be physical – as set by a Surveying, road surveyor, pictorial as in a diagram of a road or roof, or Pure mathematics, abstract. An application of the mathematical concept is found in the grade (slope), grade or gradient in geography and civil engineering. The ''steepness'', incline, or grade of a line is the absolute value of its slope: greater absolute value indicates a steeper line. The line trend is defined as follows: *An "increasing" or "ascending" line goes from left to right and has positive slope: m>0. *A "decreasing" or "descending" line goes from left to right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Todhunter
Isaac Todhunter FRS (23 November 1820 – 1 March 1884), was an English mathematician who is best known today for the books he wrote on mathematics and its history. Life and work The son of George Todhunter, a Nonconformist minister, and Mary (née Hume), he was born at Rye, Sussex. He was educated at Hastings, where his mother had opened a school after the death of his father in 1826. He was at first at a school run by Robert Carr, moving then to one opened by John Baptist Austin. Todhunter became an assistant master at a school at Peckham, attending at the same time evening classes at the University College, London where he was influenced by Augustus De Morgan. In 1842 he obtained a mathematical scholarship and graduated as B.A. at London University, where he was awarded the gold medal on the M.A. examination. About this time he became mathematical master at a school at Wimbledon. In 1844 Todhunter entered St John's College, Cambridge, where he was senior wrangl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matthew O'Brien (mathematician)
Matthew O'Brien (1814–1855) was an Irish mathematician. Life and work O'Brien was born at Ennis (county Clare) son of a medical doctor. In 1830 he was admitted in the Trinity College, Dublin, and in 1834 in the Caius College (university of Cambridge) where he graduated in 1838 as third ''wrangler'', as pupil of William Hopkins. During a brief period (1840–1841) he was fellow of Caius College. From 1844 to 1854 he was lecturer on Natural Philosophy and Mathematics at King's College London King's College London (informally King's or KCL) is a public university, public research university in London, England. King's was established by royal charter in 1829 under the patronage of George IV of the United Kingdom, King George IV ..., he simultaneously held the post of lecturer on Astronomy in the Royal Military Academy, Woolwich. O'Brien was the author of twenty mathematical papers and some elementary textbooks. His most notable contribution was in theory and ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Expression
In mathematics, an algebraic expression is an expression built up from constants (usually, algebraic numbers), variables, and the basic algebraic operations: addition (+), subtraction (-), multiplication (×), division (÷), whole number powers, and roots (fractional powers).. For example, is an algebraic expression. Since taking the square root is the same as raising to the power , the following is also an algebraic expression: :\sqrt An ''algebraic equation'' is an equation involving polynomials, for which algebraic expressions may be solutions. If you restrict your set of constants to be numbers, any algebraic expression can be called an arithmetic expression. However, algebraic expressions can be used on more abstract objects such as in Abstract algebra. If you restrict your constants to integers, the set of numbers that can be described with an algebraic expression are called Algebraic numbers. By contrast, transcendental numbers like and are not algebraic, since ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant Line
In geometry, a secant is a line (geometry), line that intersects a curve at a minimum of two distinct Point (geometry), points.. The word ''secant'' comes from the Latin word ''secare'', meaning ''to cut''. In the case of a circle, a secant intersects the circle at exactly two points. A Chord (geometry), chord is the line segment determined by the two points, that is, the interval (mathematics), interval on the secant whose ends are the two points. Circles A straight line can intersect a circle at zero, one, or two points. A line with intersections at two points is called a ''secant line'', at one point a ''tangent line'' and at no points an ''exterior line''. A ''chord'' is the line segment that joins two distinct points of a circle. A chord is therefore contained in a unique secant line and each secant line determines a unique chord. In rigorous modern treatments of plane geometry, results that seem obvious and were assumed (without statement) by Euclid in Euclid's Elements, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Curve
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane curves. Plane curves also include the Jordan curves (curves that enclose a region of the plane but need not be smooth) and the graphs of continuous functions. Symbolic representation A plane curve can often be represented in Cartesian coordinates by an implicit equation of the form f(x,y)=0 for some specific function ''f''. If this equation can be solved explicitly for ''y'' or ''x'' – that is, rewritten as y=g(x) or x=h(y) for specific function ''g'' or ''h'' – then this provides an alternative, explicit, form of the representation. A plane curve can also often be represented in Cartesian coordinates by a parametric equation of the form (x,y)=(x(t), y(t)) for specific functions x(t) and y(t). Plane curves can sometimes also be repr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |