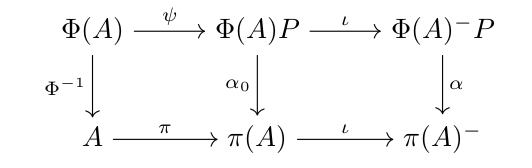|
Sherman–Takeda Theorem
In mathematics, specifically in functional analysis, the Sherman–Takeda theorem states that if ''A'' is a C*-algebra then its double dual is a W*-algebra, and is isomorphic to the weak operator topology, weak closure of ''A'' in the universal representation (C*-algebra), universal representation of ''A''. The theorem was announced by and proved by . The double dual of ''A'' is called the universal enveloping W*-algebra of ''A''. References * * Banach algebras C*-algebras Theorems in functional analysis Operator theory Von Neumann algebras {{Mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics)#Definition, norm, or Topological space#Definitions, topology) and the linear transformation, linear functions defined on these spaces and suitably respecting these structures. The historical roots of functional analysis lie in the study of function space, spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining, for example, continuous function, continuous or unitary operator, unitary operators between function spaces. This point of view turned out to be particularly useful for the study of differential equations, differential and integral equations. The usage of the word ''functional (mathematics), functional'' as a noun goes back to the calculus of v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
C*-algebra
In mathematics, specifically in functional analysis, a C∗-algebra (pronounced "C-star") is a Banach algebra together with an involution satisfying the properties of the adjoint. A particular case is that of a complex algebra ''A'' of continuous linear operators on a complex Hilbert space with two additional properties: * ''A'' is a topologically closed set in the norm topology of operators. * ''A'' is closed under the operation of taking adjoints of operators. Another important class of non-Hilbert C*-algebras includes the algebra C_0(X) of complex-valued continuous functions on ''X'' that vanish at infinity, where ''X'' is a locally compact Hausdorff space. C*-algebras were first considered primarily for their use in quantum mechanics to model algebras of physical observables. This line of research began with Werner Heisenberg's matrix mechanics and in a more mathematically developed form with Pascual Jordan around 1933. Subsequently, John von Neumann attempted to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
W*-algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. It is a special type of C*-algebra. Von Neumann algebras were originally introduced by John von Neumann, motivated by his study of single operators, group representations, ergodic theory and quantum mechanics. His double commutant theorem shows that the analytic definition is equivalent to a purely algebraic definition as an algebra of symmetries. Two basic examples of von Neumann algebras are as follows: *The ring L^\infty(\mathbb R) of essentially bounded measurable functions on the real line is a commutative von Neumann algebra, whose elements act as multiplication operators by pointwise multiplication on the Hilbert space L^2(\mathbb R) of square-integrable functions. *The algebra \mathcal B(\mathcal H) of all bounded operators on a Hilbert space \mathcal H is a von Neumann algebra, n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weak Operator Topology
In functional analysis, the weak operator topology, often abbreviated WOT,Ilijas Farah, Combinatorial Set Theory of C*-algebras' (2019), p. 80. is the weakest topology on the set of bounded operators on a Hilbert space H, such that the functional sending an operator T to the complex number \langle Tx, y\rangle is continuous for any vectors x and y in the Hilbert space. Explicitly, for an operator T there is base of neighborhoods of the following type: choose a finite number of vectors x_i, continuous functionals y_i, and positive real constants \varepsilon_i indexed by the same finite set I. An operator S lies in the neighborhood if and only if , y_i(T(x_i) - S(x_i)), 0. Relationships between different topologies on ''B(X,Y)'' The different terminology for the various topologies on B(X,Y) can sometimes be confusing. For instance, "strong convergence" for vectors in a normed space sometimes refers to norm-convergence, which is very often distinct from (and stronger than) tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Representation (C*-algebra)
In the theory of C*-algebras, the universal representation of a C*-algebra is a faithful representation which is the direct sum of the GNS representations corresponding to the states of the C*-algebra. The various properties of the universal representation are used to obtain information about the ideals and quotients of the C*-algebra. The close relationship between an arbitrary representation of a C*-algebra and its universal representation can be exploited to obtain several criteria for determining whether a linear functional on the algebra is ultraweakly continuous. The method of using the properties of the universal representation as a tool to prove results about the C*-algebra and its representations is commonly referred to as ''universal representation techniques'' in the literature. Formal definition and properties :Definition. Let ''A'' be a C*-algebra with state space ''S''. The representation ::\Phi := \bigoplus_ \pi_\rho :on the Hilbert space H_ is known as the univer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Enveloping W*-algebra
In operator algebras, the enveloping von Neumann algebra of a C*-algebra is a von Neumann algebra that contains all the operator-algebraic information about the given C*-algebra. This may also be called the ''universal'' enveloping von Neumann algebra, since it is given by a universal property; and (as always with von Neumann algebras) the term ''W*-algebra'' may be used in place of ''von Neumann algebra''. Definition Let ''A'' be a C*-algebra and ''π''''U'' be its universal representation, acting on Hilbert space ''H''''U''. The image of ''π''''U'', ''π''''U''(''A''), is a C*-subalgebra of bounded operators on ''H''''U''. The enveloping von Neumann algebra of ''A'' is the closure of ''π''''U''(''A'') in the weak operator topology. It is sometimes denoted by ''A''′′. Properties The universal representation ''π''''U'' and ''A''′′ satisfies the following universal property: for any representation ''π'', there is a unique *-homomorphis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe became the first president while Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance over concerns about competing with the '' American Journal of Mathematics''. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Algebras
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers (or over a non-Archimedean complete normed field) that at the same time is also a Banach space, that is, a normed space that is complete in the metric induced by the norm. The norm is required to satisfy \, x \, y\, \ \leq \, x\, \, \, y\, \quad \text x, y \in A. This ensures that the multiplication operation is continuous with respect to the metric topology. A Banach algebra is called ''unital'' if it has an identity element for the multiplication whose norm is 1, and ''commutative'' if its multiplication is commutative. Any Banach algebra A (whether it is unital or not) can be embedded isometrically into a unital Banach algebra A_e so as to form a closed ideal of A_e. Often one assumes ''a priori'' that the algebra under consideration is unital because one can develop much of the theory by considering A_e and then a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
C*-algebras
In mathematics, specifically in functional analysis, a C∗-algebra (pronounced "C-star") is a Banach algebra together with an involution satisfying the properties of the adjoint. A particular case is that of a complex algebra ''A'' of continuous linear operators on a complex Hilbert space with two additional properties: * ''A'' is a topologically closed set in the norm topology of operators. * ''A'' is closed under the operation of taking adjoints of operators. Another important class of non-Hilbert C*-algebras includes the algebra C_0(X) of complex-valued continuous functions on ''X'' that vanish at infinity, where ''X'' is a locally compact Hausdorff space. C*-algebras were first considered primarily for their use in quantum mechanics to model algebras of physical observables. This line of research began with Werner Heisenberg's matrix mechanics and in a more mathematically developed form with Pascual Jordan around 1933. Subsequently, John von Neumann attempted to establis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorems In Functional Analysis
In mathematics and formal logic, a theorem is a statement that has been proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems. In mainstream mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice (ZFC), or of a less powerful theory, such as Peano arithmetic. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' and ''corollary'' for less important theorems. In mathematical logic, the concepts of theorems and proofs have been formalized in order to allow mathematical reasoni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator Theory
In mathematics, operator theory is the study of linear operators on function spaces, beginning with differential operators and integral operators. The operators may be presented abstractly by their characteristics, such as bounded linear operators or closed operators, and consideration may be given to nonlinear operators. The study, which depends heavily on the topology of function spaces, is a branch of functional analysis. If a collection of operators forms an algebra over a field, then it is an operator algebra. The description of operator algebras is part of operator theory. Single operator theory Single operator theory deals with the properties and classification of operators, considered one at a time. For example, the classification of normal operators in terms of their spectra falls into this category. Spectrum of operators The spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides cond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |