|
Runcinated 120-cell
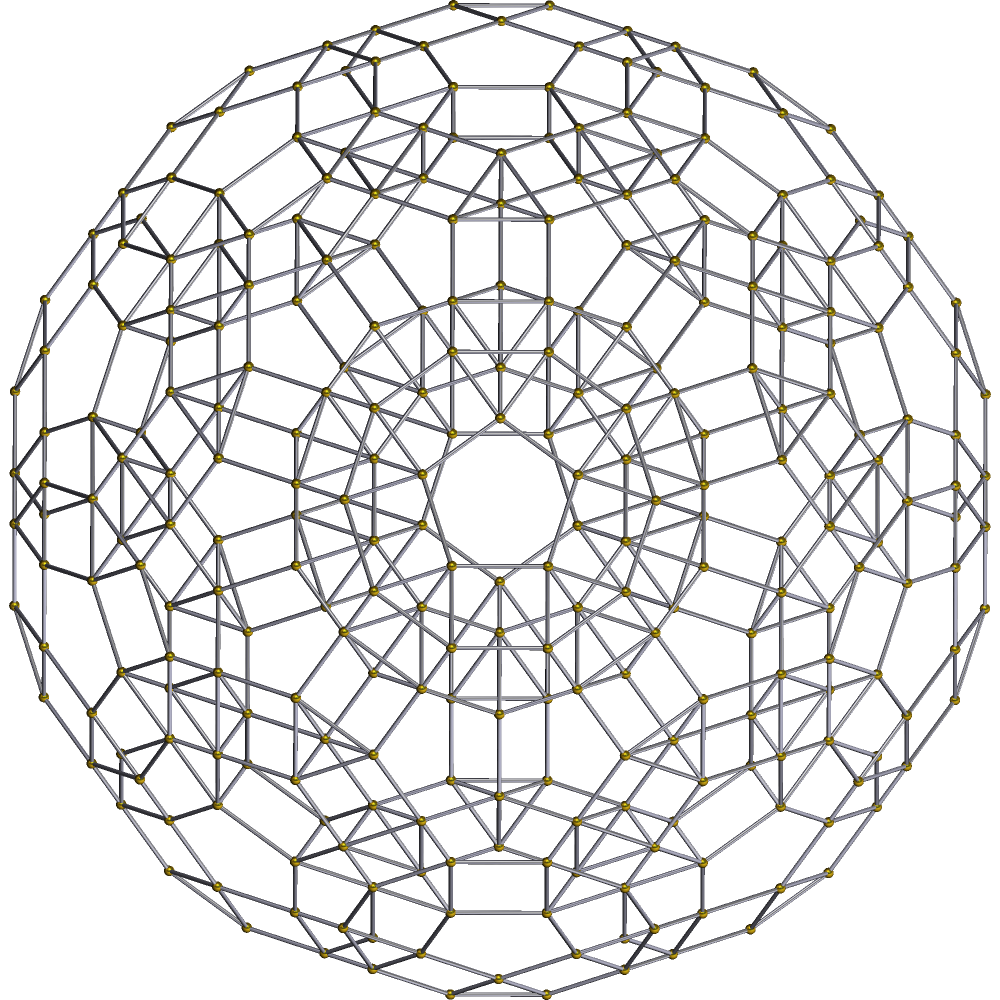
In four-dimensional geometry, a runcinated 120-cell (or ''runcinated 600-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 120-cell. There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations. The ''runcinated 120-cell'' can be seen as an expansion applied to a regular 4-polytope, the 120-cell or 600-cell. Runcinated 120-cell The runcinated 120-cell or small disprismatohexacosihecatonicosachoron is a uniform 4-polytope. It has 2640 cells: 120 dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms. Alternate names * Runcinated 120-cell / Runcinated 600-cell ( Norman W. Johnson) ** Runcinated hecatonicosachoron / Runcinated dodecac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell
In four-dimensional geometry, a runcinated 120-cell (or ''runcinated 600-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 120-cell. There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations. The ''runcinated 120-cell'' can be seen as an expansion applied to a regular 4-polytope, the 120-cell or 600-cell. Runcinated 120-cell The runcinated 120-cell or small disprismatohexacosihecatonicosachoron is a uniform 4-polytope. It has 2640 cells: 120 dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms. Alternate names * Runcinated 120-cell / Runcinated 600-cell ( Norman W. Johnson) ** Runcinated hecatonicosachoron / Runcinated dodecac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with seven faces, fifteen edges, and ten vertices. As a semiregular (or uniform) polyhedron If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a '' truncated pentagonal hosohedron'', represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a regular pentagon and a line segment, and represented by the product ×. The dual of a pentagonal prism is a pentagonal bipyramid. The symmetry group of a right pentagonal prism is ''D5h'' of order 20. The rotation group is ''D5'' of order 10. Volume The volume, as for all prisms, is the product of the area of the pentagonal base times the height or distance along any edge perpendicular to the base. For a uniform pentagonal prism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schlegel Diagram
In geometry, a Schlegel diagram is a projection of a polytope from \mathbb^d into \mathbb^ through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in \mathbb^ that, together with the original facet, is combinatorially equivalent to the original polytope. The diagram is named for Victor Schlegel, who in 1886 introduced this tool for studying combinatorial and topological properties of polytopes. In dimension 3, a Schlegel diagram is a projection of a polyhedron into a plane figure; in dimension 4, it is a projection of a 4-polytope to 3-space. As such, Schlegel diagrams are commonly used as a means of visualizing four-dimensional polytopes. Construction The most elementary Schlegel diagram, that of a polyhedron, was described by Duncan Sommerville as follows: :A very useful method of representing a convex polyhedron is by plane projection. If it is projected from any external point, since each ray cuts it twice, it wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norman Johnson (mathematician)
Norman Woodason Johnson () was a mathematician at Wheaton College, Norton, Massachusetts. Early life and education Norman Johnson was born on in Chicago. His father had a bookstore and published a local newspaper. Johnson earned his undergraduate mathematics degree in 1953 at Carleton College in Northfield, Minnesota followed by a master's degree from the University of Pittsburgh. After graduating in 1953, Johnson did alternative civilian service as a conscientious objector. He earned his PhD from the University of Toronto in 1966 with a dissertation title of ''The Theory of Uniform Polytopes and Honeycombs'' under the supervision of H. S. M. Coxeter. From there, he accepted a position in the Mathematics Department of Wheaton College in Massachusetts and taught until his retirement in 1998. Career In 1966, he enumerated 92 convex non-uniform polyhedra with regular faces. Victor Zalgaller later proved (1969) that Johnson's list was complete, and the set is now known as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694. The existence of antiprisms was discussed, and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisfy the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings or, by extension, to space-filling tessellation with polytope cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Disprismatohexacosihecatonicosachoron Net
Small may refer to: Science and technology * SMALL, an ALGOL-like programming language * Small (anatomy), the lumbar region of the back * ''Small'' (journal), a nano-science publication * <small>, an HTML element that defines smaller text Arts and entertainment Fictional characters * Small, in the British children's show Big & Small Other uses * Small, of little size * Small (surname) * "Small", a song from the album '' The Cosmos Rocks'' by Queen + Paul Rodgers See also * Smal (other) * List of people known as the Small The Small is an epithet applied to: *Bolko II the Small (c. 1312–1368), Duke of Świdnica, of Jawor and Lwówek, of Lusatia, over half of Brzeg and Oława, of Siewierz, and over half of Głogów and Ścinawa *Dionysius Exiguus (c. 470–c. 5 ... * Smalls (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of Grünbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups , and finite Coxeter groups were classified in 1935 . Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras. Standa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schläfli Symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more than three dimensions and discovered all their convex regular polytopes, including the six that occur in four dimensions. Definition The Schläfli symbol is a recursive description, starting with for a ''p''-sided regular polygon that is convex. For example, is an equilateral triangle, is a square, a convex regular pentagon, etc. Regular star polygons are not convex, and their Schläfli symbols contain irreducible fractions ''p''/''q'', where ''p'' is the number of vertices, and ''q'' is their turning number. Equivalently, is created from the vertices of , connected every ''q''. For example, is a pentagram; is a pentagon. A regular polyhedron that has ''q'' regular ''p''-sided polygon faces around each vertex is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings or, by extension, to space-filling tessellation with polytope cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |