|
Rotoreflection
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a Rotation (geometry), rotation about an axis and a reflection (mathematics), reflection in a plane perpendicular to that axis. Reflection and Point reflection, inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of Symmetry (geometry), geometric symmetry, molecular symmetry and Crystallographic point group, crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry (geometry)
In geometry, an object has symmetry if there is an Operation (mathematics), operation or Transformation (function), transformation (such as Translation (geometry), translation, Scaling (geometry), scaling, Rotation (mathematics), rotation or Reflection (mathematics), reflection) that maps the figure/object onto itself (i.e., the object has an Invariant (mathematics), invariance under the transform). Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be ''symmetric under rotation'' or to have ''rotational symmetry''. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry. The types of symmetries that are possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
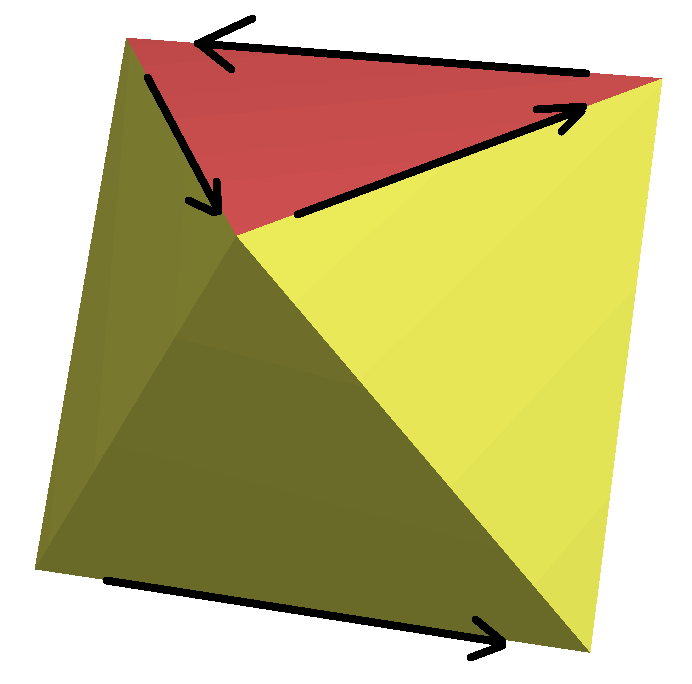
Rotoreflection Example Square Antiprism
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason it is also called a rotoinversion or rotary inversion. The two definitions are equivalent because rotation by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Symmetry
In chemistry, molecular symmetry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical property, chemical properties, such as whether or not it has a molecular dipole moment, dipole moment, as well as its allowed spectroscopy, spectroscopic transitions. To do this it is necessary to use group theory. This involves classifying the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Symmetry is useful in the study of molecular orbitals, with applications to the Hückel method, to ligand field theory, and to the Woodward–Hoffmann rules. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry discuss symmetry. Another framework on a larger scale is the use of crystal sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotoreflection Example Antiprism
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason it is also called a rotoinversion or rotary inversion. The two definitions are equivalent because rotation by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Group S4
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is invariant under some transformations, such as translation, reflection, rotation, or scaling. Although these two meanings of the word can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and nature; and in the arts, covering architecture, art, and music. The opposite of symmetry is asymmetry, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
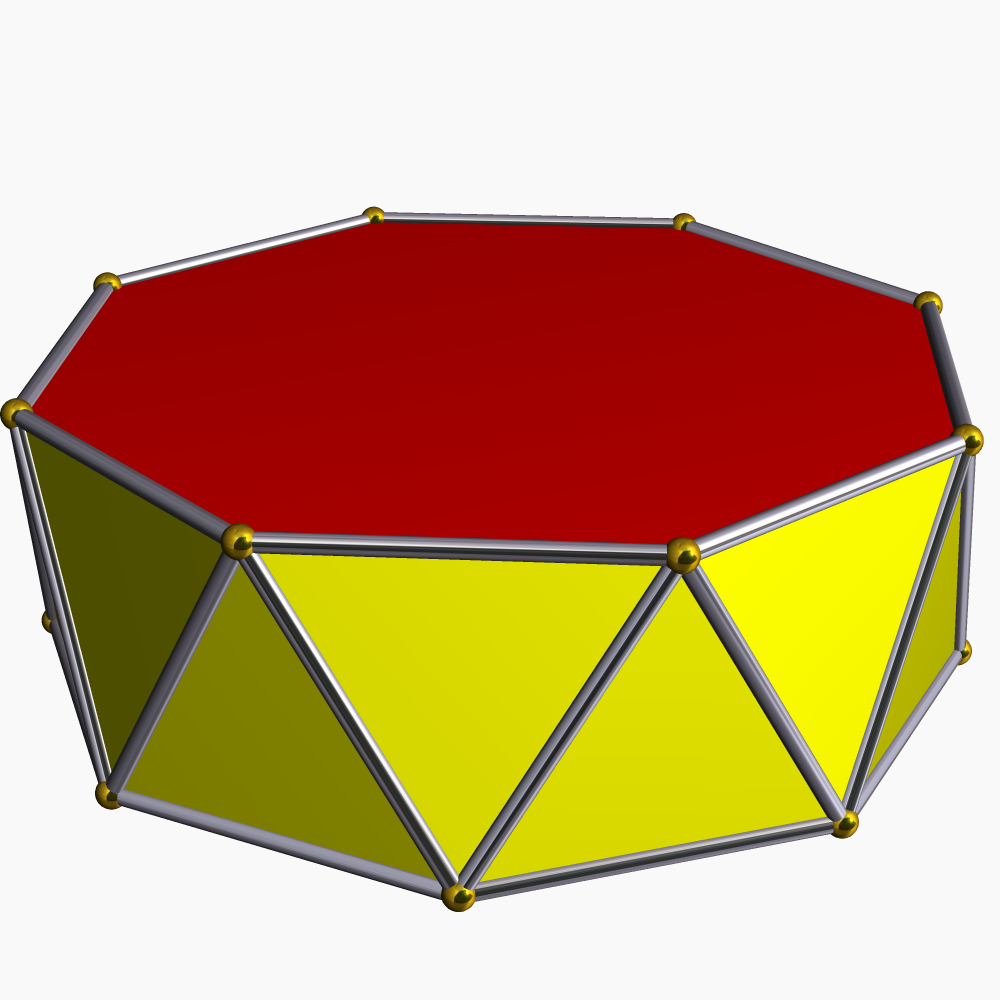
Hexagonal Antiprism
In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. Antiprisms are similar to prism (geometry), prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals. In the case of a regular ''n''-sided base, one usually considers the case where its copy is twisted by an angle . Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two bases and, connecting those bases, isosceles triangles. If faces are all regular, it is a semiregular polyhedron. Crossed antiprism A crossed hexagonal antiprism is a star polyhedron, topologically identical to the convex ''hexagonal antiprism'' with the same vertex arrangement, but it can't be made uniform; the sides are isosceles triangles. Its vertex configuration is 3.3/2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversion Symmetry
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point is reflected across a designated inversion center, which remains fixed. In Euclidean or pseudo-Euclidean spaces, a point reflection is an isometry (preserves distance). In the Euclidean plane, a point reflection is the same as a half-turn rotation (180° or radians), while in three-dimensional Euclidean space a point reflection is an improper rotation which preserves distances but reverses orientation. A point reflection is an involution: applying it twice is the identity transformation. An object that is invariant under a point reflection is said to possess point symmetry (also called inversion symmetry or central symmetry). A point group including a point reflection among its symmetries is called ''centrosymmetric''. Inversion symmetry is found in many crystal structures and molecules, and has a major effect upon their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Of Rotation
The angular displacement (symbol θ, , or φ) – also called angle of rotation, rotational displacement, or rotary displacement – of a physical body is the angle (in units of radians, degrees, turns, etc.) through which the body rotates (revolves or spins) around a centre or axis of rotation. Angular displacement may be signed, indicating the sense of rotation (e.g., clockwise); it may also be greater (in absolute value) than a full turn. Context When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time. When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is mini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Points Of Isometry Groups In Euclidean Space
A fixed point of an isometry group is a point that is a fixed point for every isometry in the group. For any isometry group in Euclidean space the set of fixed points is either empty or an affine space. For an object, any unique centre and, more generally, any point with unique properties with respect to the object is a fixed point of its symmetry group. In particular this applies for the centroid of a figure, if it exists. In the case of a physical body, if for the symmetry not only the shape but also the density is taken into account, it applies to the centre of mass. If the set of fixed points of the symmetry group of an object is a singleton then the object has a specific centre of symmetry. The centroid and centre of mass, if defined, are this point. Another meaning of "centre of symmetry" is a point with respect to which inversion symmetry applies. Such a point needs not be unique; if it is not, there is translational symmetry, hence there are infinitely many of such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |