|
Rank-dependent Expected Utility
The rank-dependent expected utility model (originally called anticipated utility) is a generalized expected utility model of choice under uncertainty, designed to explain the behaviour observed in the Allais paradox, as well as for the observation that many people both purchase lottery tickets (implying risk-loving preferences) and insure against losses (implying risk aversion). A natural explanation of these observations is that individuals overweight low-probability events such as winning the lottery, or suffering a disastrous insurable loss. In the Allais paradox, individuals appear to forgo the chance of a very large gain to avoid a one per cent chance of missing out on an otherwise certain large gain, but are less risk averse when offered the chance of reducing an 11 per cent chance of loss to 10 per cent. A number of attempts were made to model preferences incorporating probability theory, most notably the original version of prospect theory, presented by Daniel Kahneman a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Expected Utility
Generalized expected utility is a decision theory, decision-making metric based on any of a variety of theories that attempt to resolve some discrepancies between expected utility theory and empirical observations, concerning choice under risk (statistics), risky (probabilistic) or uncertain circumstances. Given its motivations and approach, generalized expected utility theory may properly be regarded as a subfield of behavioral economics, but it is more frequently located within mainstream economic theory. The expected utility model developed by John von Neumann and Oskar Morgenstern dominated decision theory from its formulation in 1944 until the late 1970s, not only as a prescriptive, but also as a descriptive model, despite powerful criticism from Maurice Allais and Daniel Ellsberg who showed that, in certain choice problems, decisions were usually inconsistent with the axioms of expected utility theory. These problems are usually referred to as the Allais paradox and Ellsberg pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty
Uncertainty or incertitude refers to situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown, and is particularly relevant for decision-making. Uncertainty arises in partially observable or stochastic environments, as well as due to ignorance, Laziness, indolence, or both. It arises in any number of fields, including insurance, philosophy, physics, statistics, economics, finance, medicine, psychology, sociology, engineering, metrology, meteorology, ecology and information science. Concepts Although the terms are used in various ways among the general public, many specialists in decision theory, statistics and other quantitative fields have defined uncertainty, risk, and their measurement as: Uncertainty The lack of certainty, a state of limited knowledge where it is impossible to exactly describe the existing state, a future outcome, or more than one possible outcome. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allais Paradox
The Allais paradox is a choice problem designed by to show an inconsistency of actual observed choices with the predictions of expected utility theory. The Allais paradox demonstrates that individuals rarely make rational decisions consistently when required to do so immediately. The independence axiom of expected utility theory, which requires that the preferences of an individual should not change when altering two lotteries by equal proportions, was proven to be violated by the paradox. Statement of the problem The Allais paradox arises when comparing participants' choices in two different experiments, each of which consists of a choice between two gambles, A and B. The payoffs for each gamble in each experiment are as follows: Several studies involving hypothetical and small monetary payoffs, and recently involving health outcomes, have supported the assertion that when presented with a choice between 1A and 1B, most people would choose 1A. Likewise, when presented with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-loving
In accounting, finance, and economics, a risk-seeker or risk-lover is a person who has a preference ''for'' risk. While most investors are considered risk ''averse'', one could view casino-goers as risk-seeking. A common example to explain risk-seeking behaviour is; If offered two choices; either $50 as a sure thing, or a 50% chance each of either $100 or nothing, a risk-seeking person would prefer the gamble. Even though the gamble and the "sure thing" have the same expected value, the preference for risk makes the gamble's expected utility for the individual much higher. The Utility Function and Risk-Seekers Choice under uncertainty is when a person facing a choice is not certain of the possible outcomes or their probability of occurring. The standard way to model how people choose under uncertain condition, is by using expected utility. In order to calculate expected utility, a utility function 'u' is developed in order to translate money into Utility. Therefore, if a person ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk Aversion
In economics and finance, risk aversion is the tendency of people to prefer outcomes with low uncertainty to those outcomes with high uncertainty, even if the average outcome of the latter is equal to or higher in monetary value than the more certain outcome. Risk aversion explains the inclination to agree to a situation with a lower average payoff that is more predictable rather than another situation with a less predictable payoff that is higher on average. For example, a risk-averse investor might choose to put their money into a bank account with a low but guaranteed interest rate, rather than into a stock that may have high expected returns, but also involves a chance of losing value. Example A person is given the choice between two scenarios: one with a guaranteed payoff, and one with a risky payoff with same average value. In the former scenario, the person receives $50. In the uncertain scenario, a coin is flipped to decide whether the person receives $100 or nothing. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
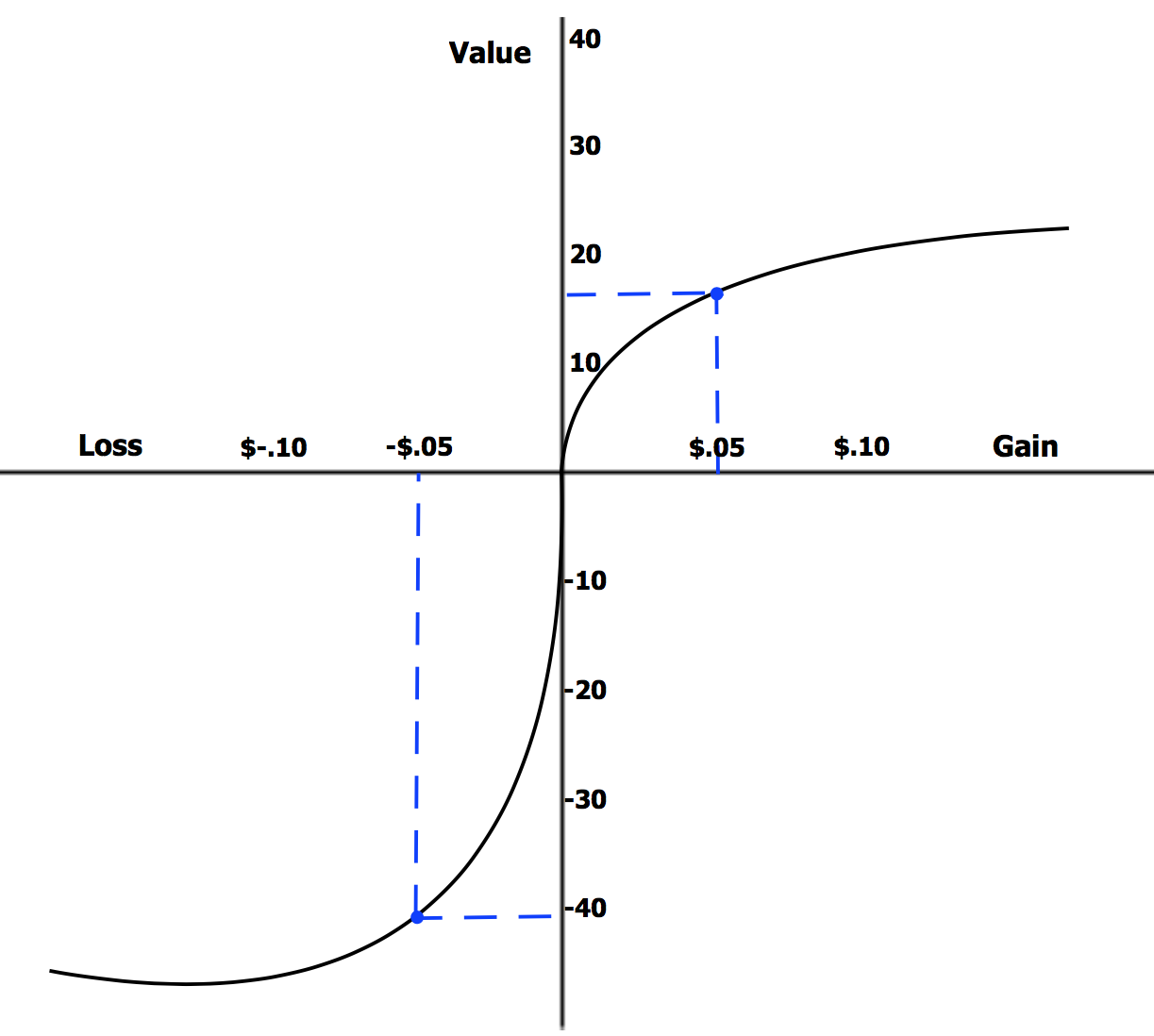
Prospect Theory
Prospect theory is a theory of behavioral economics, judgment and decision making that was developed by Daniel Kahneman and Amos Tversky in 1979. The theory was cited in the decision to award Kahneman the 2002 Nobel Memorial Prize in Economics. Based on results from controlled studies, it describes how individuals assess their loss and gain perspectives in an asymmetric manner (see loss aversion). For example, for some individuals, the pain from losing $1,000 could only be compensated by the pleasure of earning $2,000. Thus, contrary to the expected utility theory (which models the decision that perfectly rational agents would make), prospect theory aims to describe the actual behavior of people. In the original formulation of the theory, the term ''prospect'' referred to the predictable results of a lottery. However, prospect theory can also be applied to the prediction of other forms of behaviors and decisions. Prospect theory challenges the expected utility theory deve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Kahneman
Daniel Kahneman (; ; March 5, 1934 – March 27, 2024) was an Israeli-American psychologist best known for his work on the psychology of judgment and decision-making as well as behavioral economics, for which he was awarded the 2002 Nobel Memorial Prize in Economic Sciences together with Vernon L. Smith. Kahneman's published empirical findings challenge the assumption of human rationality prevailing in modern economic theory. Kahneman became known as the "grandfather of behavioral economics." With Amos Tversky and others, Kahneman established a cognitive basis for common human errors that arise from heuristics and biases, and developed prospect theory. In 2011, Kahneman was named by ''Foreign Policy'' magazine in its list of top global thinkers. In the same year, his book '' Thinking, Fast and Slow'', which summarizes much of his research, was published and became a best seller. In 2015, ''The Economist'' listed him as the seventh most influential economist in the world. Kah ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amos Tversky
Amos Nathan Tversky (; March 16, 1937 – June 2, 1996) was an Israeli cognitive and mathematical psychologist and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement. He was co-author of a three-volume treatise, ''Foundations of Measurement''. His early work with Daniel Kahneman focused on the psychology of prediction and probability judgment; later they worked together to develop prospect theory, which aims to explain irrational human economic choices and is considered one of the seminal works of behavioral economics. Six years after Tversky's death, Kahneman received the 2002 Nobel Memorial Prize in Economic Sciences for work he did in collaboration with Amos Tversky. While Nobel Prizes are not awarded posthumously, Kahneman has commented that he feels "it is a joint prize. We were twinned for more than a decade." Tversky also collaborated with many leading researchers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Dominance
Stochastic dominance is a Partially ordered set, partial order between random variables. It is a form of stochastic ordering. The concept arises in decision theory and decision analysis in situations where one gamble (a probability distribution over possible outcomes, also known as prospects) can be ranked as superior to another gamble for a broad class of decision-makers. It is based on shared preference (economics), preferences regarding sets of possible outcomes and their associated probabilities. Only limited knowledge of preferences is required for determining dominance. Risk aversion is a factor only in second order stochastic dominance. Stochastic dominance does not give a total order, but rather only a partial order: for some pairs of gambles, neither one stochastically dominates the other, since different members of the broad class of decision-makers will differ regarding which gamble is preferable without them generally being considered to be equally attractive. Through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Relation
In mathematics, a binary relation on a set (mathematics), set is transitive if, for all elements , , in , whenever relates to and to , then also relates to . Every partial order and every equivalence relation is transitive. For example, less than and equality (mathematics), equality among real numbers are both transitive: If and then ; and if and then . Definition A homogeneous relation on the set is a ''transitive relation'' if, :for all , if and , then . Or in terms of first-order logic: :\forall a,b,c \in X: (aRb \wedge bRc) \Rightarrow aRc, where is the infix notation for . Examples As a non-mathematical example, the relation "is an ancestor of" is transitive. For example, if Amy is an ancestor of Becky, and Becky is an ancestor of Carrie, then Amy is also an ancestor of Carrie. On the other hand, "is the birth mother of" is not a transitive relation, because if Alice is the birth mother of Brenda, and Brenda is the birth mother of Claire, then it does ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |