|
Quantum Calculus
Quantum calculus, sometimes called calculus without limits, is equivalent to traditional infinitesimal calculus without the notion of limits. The two types of calculus in quantum calculus are ''q''-calculus and ''h''-calculus. The goal of both types is to find "analogs" of mathematical objects, where, after taking a certain limit, the original object is returned. In ''q''-calculus, the limit as ''q'' tends to 1 is taken of the ''q''-analog. Likewise, in ''h''-calculus, the limit as h tends to 0 is taken of the ''h''-analog. The parameters q and h can be related by the formula q = e^h. Differentiation The ''q''-differential and ''h''-differential are defined as: :d_q(f(x)) = f(qx) - f(x) and :d_h(f(x)) = f(x + h) - f(x), respectively. The ''q''-derivative and ''h''-derivative are then defined as :D_q(f(x)) = \frac = \frac and :D_h(f(x)) = \frac = \frac respectively. By taking the limit as q \rightarrow 1 of the ''q''-derivative or as h \rightarrow 0 of the ''h''-derivati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal Calculus
Calculus is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence of infinite sequences and infinite series to a well-defined limit. It is the "mathematical backbone" for dealing with problems where variables change with time or another reference variable. Infinitesimal calculus was formulated separately in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Later work, including codifying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Boole
George Boole ( ; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in Ireland. He worked in the fields of differential equations and algebraic logic, and is best known as the author of ''The Laws of Thought'' (1854), which contains Boolean algebra. Boolean logic, essential to computer programming, is credited with helping to lay the foundations for the Information Age. Boole was the son of a shoemaker. He received a primary school education and learned Latin and modern languages through various means. At 16, he began teaching to support his family. He established his own school at 19 and later ran a boarding school in Lincoln. Boole was an active member of local societies and collaborated with fellow mathematicians. In 1849, he was appointed the first professor of mathematics at Queen's College, Cork (now University C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Dilogarithm
In mathematics, the quantum dilogarithm is a special function defined by the formula : \phi(x)\equiv(x;q)_\infty=\prod_^\infty (1-xq^n),\quad , q, 0. References * * * * * * * External links * {{nlab, id=quantum+dilogarithm, title=quantum dilogarithm Special functions Q-analogs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basic Hypergeometric Series
In mathematics, basic hypergeometric series, or ''q''-hypergeometric series, are q-analog, ''q''-analogue generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series ''x''''n'' is called hypergeometric if the ratio of successive terms ''x''''n''+1/''x''''n'' is a rational function of ''n''. If the ratio of successive terms is a rational function of ''q''''n'', then the series is called a basic hypergeometric series. The number ''q'' is called the base. The basic hypergeometric series _2\phi_1(q^,q^;q^;q,x) was first considered by . It becomes the hypergeometric series F(\alpha,\beta;\gamma;x) in the limit when base q =1. Definition There are two forms of basic hypergeometric series, the unilateral basic hypergeometric series φ, and the more general bilateral basic hypergeometric series ψ. The unilateral basic hypergeometric series is defined as :\;_\phi_k \left[\begin a_1 & a_2 & \ldots & a_ \\ b_1 & b_2 & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
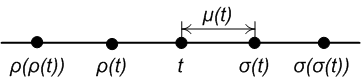
Time Scale Calculus
In mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid systems. It has applications in any field that requires simultaneous modelling of Discrete time and continuous time, discrete and continuous data. It gives a new definition of a derivative such that if one differentiates a function defined on the real numbers then the definition is equivalent to standard differentiation, but if one uses a function defined on the integers then it is equivalent to the forward difference operator. History Time-scale calculus was introduced in 1988 by the German mathematician Stefan Hilger. However, similar ideas have been used before and go back at least to the introduction of the Riemann–Stieltjes integral, which unifies sums and integrals. Dynamic equations Many results concerning differential e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Differential Calculus
In quantum geometry or noncommutative geometry a quantum differential calculus or noncommutative differential structure on an algebra A over a field k means the specification of a space of differential forms over the algebra. The algebra A here is regarded as a coordinate ring but it is important that it may be noncommutative and hence not an actual algebra of coordinate functions on any actual space, so this represents a point of view replacing the specification of a differentiable structure for an actual space. In ordinary differential geometry one can multiply differential 1-forms by functions from the left and from the right, and there exists an exterior derivative. Correspondingly, a first order quantum differential calculus means at least the following: # An A-A-bimodule \Omega^1 over A, i.e. one can multiply elements of \Omega^1 by elements of A in an associative way: a(\omega b)=(a\omega)b,\ \forall a,b\in A,\ \omega\in\Omega^1 . # A linear map :A\to\Omega^1 obeying the Le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noncommutative Geometry
Noncommutative geometry (NCG) is a branch of mathematics concerned with a geometric approach to noncommutative algebras, and with the construction of ''spaces'' that are locally presented by noncommutative algebras of functions, possibly in some generalized sense. A noncommutative algebra is an associative algebra in which the multiplication is not commutative, that is, for which xy does not always equal yx; or more generally an algebraic structure in which one of the principal binary operations is not commutative; one also allows additional structures, e.g. topology or norm, to be possibly carried by the noncommutative algebra of functions. An approach giving deep insight about noncommutative spaces is through operator algebras, that is, algebras of bounded linear operators on a Hilbert space. Perhaps one of the typical examples of a noncommutative space is the " noncommutative torus", which played a key role in the early development of this field in 1980s and lead to noncomm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Group
In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups (which are quasitriangular Hopf algebras), compact matrix quantum groups (which are structures on unital separable C*-algebras), and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group. The term "quantum group" first appeared in the theory of quantum integrable systems, which was then formalized by Vladimir Drinfeld and Michio Jimbo as a particular class of Hopf algebra. The same term is also used for other Hopf algebras that deform or are close to classical Lie groups or Lie algebras, such as a "bicrossproduct" class of quantum groups introduced by Shahn Majid a little after the work of Drinfeld and Jimbo. In Drinfeld's approach, quantum groups arise as Hopf algebras depe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identity. In other words, a Lie algebra is an algebra over a field for which the multiplication operation (called the Lie bracket) is alternating and satisfies the Jacobi identity. The Lie bracket of two vectors x and y is denoted ,y/math>. A Lie algebra is typically a non-associative algebra. However, every associative algebra gives rise to a Lie algebra, consisting of the same vector space with the commutator Lie bracket, ,y= xy - yx . Lie algebras are closely related to Lie groups, which are groups that are also smooth manifolds: every Lie group gives rise to a Lie algebra, which is the tangent space at the identity. (In this case, the Lie bracket measures the failure of commutativity for the Lie group.) Conversely, to any finite-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Gustav Jacobi
Carl Gustav Jacob Jacobi (; ; 10 December 1804 – 18 February 1851) was a German mathematician who made fundamental contributions to elliptic functions, dynamics, differential equations, determinants and number theory. Biography Jacobi was born of Ashkenazi Jewish parentage in Potsdam on 10 December 1804. He was the second of four children of a banker, Simon Jacobi. His elder brother, Moritz, would also become known later as an engineer and physicist. He was initially home schooled by his uncle Lehman, who instructed him in the classical languages and elements of mathematics. In 1816, the twelve-year-old Jacobi went to the Potsdam Gymnasium, where students were taught all the standard subjects: classical languages, history, philology, mathematics, sciences, etc. As a result of the good education he had received from his uncle, as well as his own remarkable abilities, after less than half a year Jacobi was moved to the senior year despite his young age. However, as the Univ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and Mathematical notation, notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Kingdom of Prussia, Prussia. Euler is credited for popularizing the Greek letter \pi (lowercase Pi (letter), pi) to denote Pi, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |