|
Production Function
In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream economics, mainstream neoclassical economics, neoclassical theories, used to define marginal product and to distinguish allocative efficiency, a key focus of economics. One important purpose of the production function is to address allocative efficiency in the use of factor inputs in production and the resulting distribution of income to those factors, while abstracting away from the technological problems of achieving technical efficiency, as an engineer or professional manager might understand it. For modelling the case of many outputs and many inputs, researchers often use the so-called Shephard's distance functions or, alternatively, directional distance functions, which are generalizations of the simple production function in economics. In macroeconomics, aggregate produc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Factor Productivity
In economics, total-factor productivity (TFP), also called multi-factor productivity, is usually measured as the ratio of aggregate output (e.g., GDP) to aggregate inputs. Under some simplifying assumptions about the production technology, growth in TFP becomes the portion of growth in output not explained by growth in traditionally measured inputs of labour and capital used in production. TFP is calculated by dividing output by the weighted geometric average of labour and capital input, with the standard weighting of 0.7 for labour and 0.3 for capital. Total factor productivity is a measure of productive efficiency in that it measures how much output can be produced from a certain amount of inputs. It accounts for part of the differences in cross-country per-capita income. For relatively small percentage changes, the rate of ''TFP'' growth can be estimated by subtracting growth rates of labor and capital inputs from the growth rate of output. Background Technology growth and e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joan Robinson
Joan Violet Robinson ( Maurice; 31 October 1903 – 5 August 1983) was a British economist known for her wide-ranging contributions to economic theory. One of the most prominent economists of the century, Robinson incarnated the "Cambridge School" in most of its guises in the 20th century. She started out as a Marshallian, became one of the earliest and most ardent Keynesians after 1936, and ended up as a leader of the neo-Ricardian and post-Keynesian schools. Early life and education Before leaving to fight in the Second Boer War, Joan's father, Frederick Maurice, married Margaret Helen Marsh, the daughter of Frederick Howard Marsh, and the sister of Edward Marsh, at St George's, Hanover Square. Joan Violet Maurice was born in 1903, a year after her father's return from Africa, the third of five siblings. Joan Maurice studied economics at Girton College, Cambridge. She completed her studies in 1925 but due to Cambridge University's refusal to grant degrees to women u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capital Controversy
The Cambridge capital controversy, sometimes called "the capital controversy"Brems (1975) pp. 369–384 or "the two Cambridges debate", was a dispute between proponents of two differing theoretical and mathematical positions in economics that started in the 1950s and lasted well into the 1960s. The debate concerned the nature and role of capital goods and a critique of the neoclassical vision of aggregate production and distribution.Tcherneva (2011) The name arises from the location of the principals involved in the controversy: the debate was largely between economists such as Joan Robinson and Piero Sraffa at the University of Cambridge in England and economists such as Paul Samuelson and Robert Solow at the Massachusetts Institute of Technology, in Cambridge, Massachusetts, United States. The English side is most often labeled " post-Keynesian", while some call it " neo-Ricardian", and the Massachusetts side " neoclassical". Most of the debate is mathematical, while some maj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
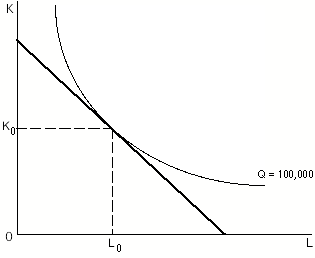
Isoquant
An isoquant (derived from ''quantity'' and the Greek word ', , meaning "equal"), in microeconomics, is a contour line drawn through the set of points at which the same quantity of output is produced while changing the quantities of two or more inputs. The x and y axis on an isoquant represent two relevant inputs, which are usually a factor of production such as labour, capital, land, or organisation. An isoquant may also be known as an "iso-product curve", or an "equal product curve". Vs. indifference curves While an indifference curve mapping helps to solve the utility-maximizing problem of consumers, the isoquant mapping deals with the cost-minimization and profit and output maximisation problem of producers. Indifference curves further differ to isoquants, in that they cannot offer a precise measurement of utility, only how it is relevant to a baseline. Whereas, from an isoquant, the product can be measured accurately in physical units, and it is known by exactly how much iso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Returns To Scale
In economics, the concept of returns to scale arises in the context of a firm's production function. It explains the long-run linkage of increase in output (production) relative to associated increases in the inputs (factors of production). In the long run, all factors of production are variable and subject to change in response to a given increase in production scale. In other words, returns to scale analysis is a long-term theory because a company can only change the scale of production in the long run by changing factors of production, such as building new facilities, investing in new machinery, or improving technology. There are three possible types of returns to scale: * If output increases by the same proportional change as all inputs change then there are constant returns to scale (CRS). For example, when inputs (labor and capital) increase by 100%, output increases by 100%. * If output increases by less than the proportional change in all inputs, there are decreasing retu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
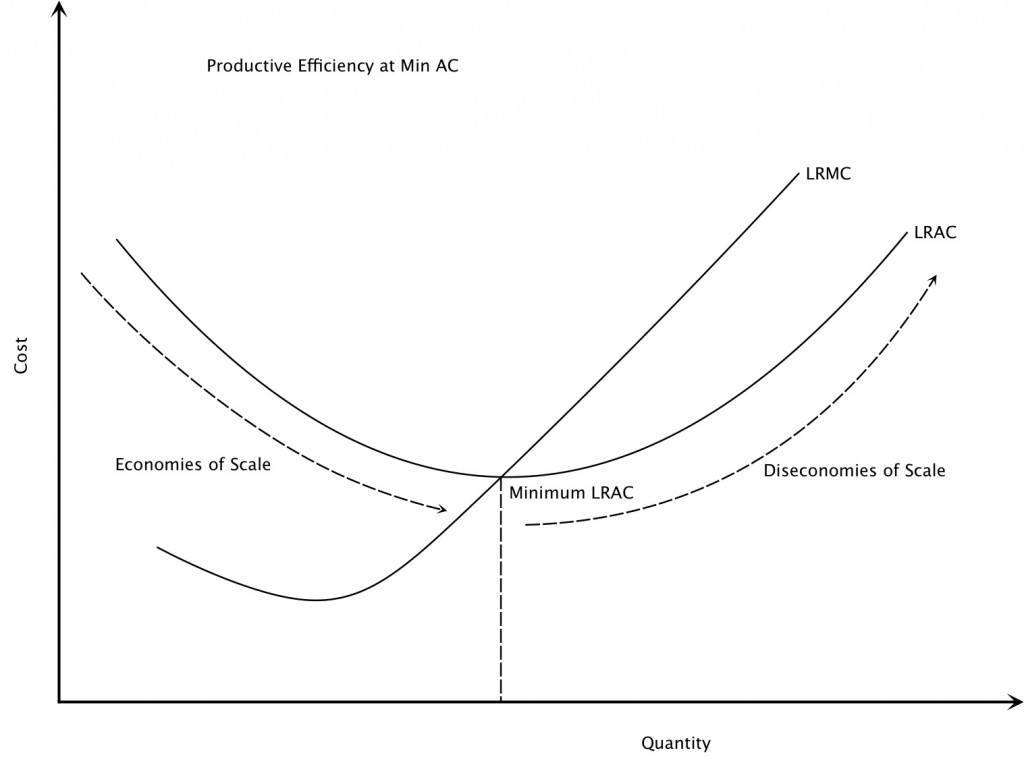
Diseconomy Of Scale
In microeconomics, diseconomies of scale are the cost disadvantages that economic actors accrue due to an increase in organizational size or in output, resulting in production of goods and services at increased per-unit costs. The concept of diseconomies of scale is the opposite of economies of scale. It occurs when economies of scale become dysfunctional for a firm. In business, diseconomies of scale are the features that lead to an increase in average costs as a business grows beyond a certain size. Causes Communication costs Ideally, all employees of a firm would have one-on-one communication with each other so they know exactly what the other workers are doing. A firm with a single worker does not require any communication between employees. A firm with two workers requires one communication channel, directly between those two workers. A firm with three workers requires three communication channels between employees (between employees A & B, B & C, and A & C). Here is a char ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Returns To Scale
In economics, the concept of returns to scale arises in the context of a firm's production function. It explains the long-run linkage of increase in output (production) relative to associated increases in the inputs (factors of production). In the long run, all factors of production are variable and subject to change in response to a given increase in production scale. In other words, returns to scale analysis is a long-term theory because a company can only change the scale of production in the long run by changing factors of production, such as building new facilities, investing in new machinery, or improving technology. There are three possible types of returns to scale: * If output increases by the same proportional change as all inputs change then there are constant returns to scale (CRS). For example, when inputs (labor and capital) increase by 100%, output increases by 100%. * If output increases by less than the proportional change in all inputs, there are decreasing retu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economy Of Scale
In microeconomics, economies of scale are the cost advantages that enterprises obtain due to their scale of operation, and are typically measured by the amount of output produced per unit of cost (production cost). A decrease in cost per unit of output enables an increase in scale that is, increased production with lowered cost. At the basis of economies of scale, there may be technical, statistical, organizational or related factors to the degree of market control. Economies of scale arise in a variety of organizational and business situations and at various levels, such as a production, plant or an entire enterprise. When average costs start falling as output increases, then economies of scale occur. Some economies of scale, such as capital cost of manufacturing facilities and friction loss of transportation and industrial equipment, have a physical or engineering basis. The economic concept dates back to Adam Smith and the idea of obtaining larger production returns thro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Function
In mathematics, a homogeneous function is a function of several variables such that the following holds: If each of the function's arguments is multiplied by the same scalar (mathematics), scalar, then the function's value is multiplied by some power of this scalar; the power is called the degree of homogeneity, or simply the ''degree''. That is, if is an integer, a function of variables is homogeneous of degree if :f(sx_1,\ldots, sx_n)=s^k f(x_1,\ldots, x_n) for every x_1, \ldots, x_n, and s\ne 0. This is also referred to a ''th-degree'' or ''th-order'' homogeneous function. For example, a homogeneous polynomial of degree defines a homogeneous function of degree . The above definition extends to functions whose domain of a function, domain and codomain are vector spaces over a Field (mathematics), field : a function f : V \to W between two -vector spaces is ''homogeneous'' of degree k if for all nonzero s \in F and v \in V. This definition is often further generalized to f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shifting Production Function Small
Shift may refer to: Art, entertainment, and media Gaming * ''Shift'' (series), a 2008 online video game series by Armor Games * '' Need for Speed: Shift'', a 2009 racing video game ** '' Shift 2: Unleashed'', its 2011 sequel Literature * ''Shift'' (novel), a 2010 alternative history book by Tim Kring and Dale Peck * ''Shift'' (novella), a 2013 science fiction book, part two of the Silo trilogy by Hugh Howey * Shift the Ape, a character in ''The Chronicles of Narnia'' novel series * Shift (DC Comics), a DC Comics character who is a fragment of Metamorpho * Shift (Marvel Comics), a Marvel Comics character who is a clone of Miles Morales Music * ''Shift'' (Nasum album), 2004 * Shift (The Living End album) * Shift (music), a change of level in music * Shift (string technique), a finger movement from one position to another on the same string Other uses in arts, entertainment, and media * ''Shift'' (magazine), a former Canadian technology and culture magazine * Shift ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
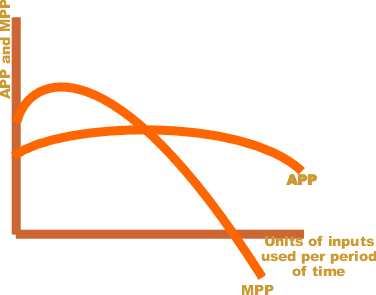
Marginal Physical Product
In economics and in particular neoclassical economics, the marginal product or marginal physical productivity of an input (factor of production) is the change in output resulting from employing one more unit of a particular input (for instance, the change in output when a firm's labor is increased from five to six units), assuming that the quantities of other inputs are kept constant. The marginal product of a given input can be expressed as: :MP = \frac where \Delta X is the change in the firm's use of the input (conventionally a one-unit change) and \Delta Y is the change in the quantity of output produced (resulting from the change in the input). Note that the quantity Y of the "product" is typically defined ignoring externalities, external costs and benefits. If the output and the input are infinitely divisible, so the marginal "units" are infinitesimal, the marginal product is the mathematical derivative of the production function with respect to that input. Suppose a fir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |