|
Probability Measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint (mutually exclusive) events by the measure should be the sum of the probabilities of the events; for example, the value assigned to the outcome "1 or 2" in a throw of a dice should be the sum of the values assigned to the outcomes "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a set function \mu to be a probability measure on a σ-algebra are that: * \mu must return results in the unit interval , 1 returning 0 fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often by help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hindman’s Theorem
In mathematics, an IP set is a set of natural numbers which contains all finite sums of some infinite set. The finite sums of a set ''D'' of natural numbers are all those numbers that can be obtained by adding up the elements of some finite nonempty subset of ''D''. The set of all finite sums over ''D'' is often denoted as FS(''D''). Slightly more generally, for a sequence of natural numbers (''n''i), one can consider the set of finite sums FS((''n''i)), consisting of the sums of all finite length subsequences of (''n''i). A set ''A'' of natural numbers is an IP set if there exists an infinite set ''D'' such that FS(''D'') is a subset of ''A''. Equivalently, one may require that ''A'' contains all finite sums FS((''n''i)) of a sequence (''n''i). Some authors give a slightly different definition of IP sets: They require that FS(''D'') equal ''A'' instead of just being a subset. The term IP set was coined by Hillel Furstenberg and Benjamin Weiss to abbreviate "infinite-dimensio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultrafilter
In the mathematical field of order theory, an ultrafilter on a given partially ordered set (or "poset") P is a certain subset of P, namely a maximal filter on P; that is, a proper filter on P that cannot be enlarged to a bigger proper filter on P. If X is an arbitrary set, its power set \wp(X), ordered by set inclusion, is always a Boolean algebra and hence a poset, and ultrafilters on \wp(X) are usually called X.If X happens to be partially ordered, too, particular care is needed to understand from the context whether an (ultra)filter on \wp(X) or an (ultra)filter just on X is meant; both kinds of (ultra)filters are quite different. Some authors use "(ultra)filter" ''of'' a partial ordered set" vs. "''on'' an arbitrary set"; i.e. they write "(ultra)filter on X" to abbreviate "(ultra)filter of \wp(X)". An ultrafilter on a set X may be considered as a finitely additive measure on X. In this view, every subset of X is either considered " almost everything" (has measure 1) or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amino Acid
Amino acids are organic compounds that contain both amino and carboxylic acid functional groups. Although hundreds of amino acids exist in nature, by far the most important are the alpha-amino acids, which comprise proteins. Only 22 alpha amino acids appear in the genetic code. Amino acids can be classified according to the locations of the core structural functional groups, as Alpha and beta carbon, alpha- , beta- , gamma- or delta- amino acids; other categories relate to Chemical polarity, polarity, ionization, and side chain group type (aliphatic, Open-chain compound, acyclic, aromatic, containing hydroxyl or sulfur, etc.). In the form of proteins, amino acid ''residues'' form the second-largest component ( water being the largest) of human muscles and other tissues. Beyond their role as residues in proteins, amino acids participate in a number of processes such as neurotransmitter transport and biosynthesis. It is thought that they played a key role in enabling li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence Analysis
In bioinformatics, sequence analysis is the process of subjecting a DNA, RNA or peptide sequence to any of a wide range of analytical methods to understand its features, function, structure, or evolution. Methodologies used include sequence alignment, searches against biological databases, and others. Since the development of methods of high-throughput production of gene and protein sequences, the rate of addition of new sequences to the databases increased very rapidly. Such a collection of sequences does not, by itself, increase the scientist's understanding of the biology of organisms. However, comparing these new sequences to those with known functions is a key way of understanding the biology of an organism from which the new sequence comes. Thus, sequence analysis can be used to assign function to genes and proteins by the study of the similarities between the compared sequences. Nowadays, there are many tools and techniques that provide the sequence comparisons (sequence a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Biology
Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of the living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to prove and validate the scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms are sometimes interchanged. Mathematical biology aims at the mathematical representation and modeling of biological processes, using techniques and tools of applied mathematics. It can be useful in both theoretical and pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congruence Relation
In abstract algebra, a congruence relation (or simply congruence) is an equivalence relation on an algebraic structure (such as a group, ring, or vector space) that is compatible with the structure in the sense that algebraic operations done with equivalent elements will yield equivalent elements. Every congruence relation has a corresponding quotient structure, whose elements are the equivalence classes (or congruence classes) for the relation. Basic example The prototypical example of a congruence relation is congruence modulo n on the set of integers. For a given positive integer n, two integers a and b are called congruent modulo n, written : a \equiv b \pmod if a - b is divisible by n (or equivalently if a and b have the same remainder when divided by n). For example, 37 and 57 are congruent modulo 10, : 37 \equiv 57 \pmod since 37 - 57 = -20 is a multiple of 10, or equivalently since both 37 and 57 have a remainder of 7 when divided by 10. Congruence modulo n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Market
In economics, a complete market (aka Arrow-Debreu market or complete system of markets) is a market with two conditions: # Negligible transaction costs and therefore also perfect information, # there is a price for every asset in every possible state of the world In such a market, the complete set of possible bets on future states of the world can be constructed with existing assets without friction. Here, goods are state-contingent; that is, a good includes the time and state of the world in which it is consumed. For instance, an umbrella tomorrow if it rains is a distinct good from an umbrella tomorrow if it is clear. The study of complete markets is central to state-preference theory. The theory can be traced to the work of Kenneth Arrow (1964), Gérard Debreu (1959), Arrow & Debreu (1954) and Lionel McKenzie (1954). Arrow and Debreu were awarded the Nobel Memorial Prize in Economics (Arrow in 1972, Debreu in 1983), largely for their work in developing the theory of complete ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-free Rate
The risk-free rate of return, usually shortened to the risk-free rate, is the rate of return of a hypothetical investment with scheduled payments over a fixed period of time that is assumed to meet all payment obligations. Since the risk-free rate can be obtained with no risk, any other investment having some risk will have to have a higher rate of return in order to induce any investors to hold it. In practice, to infer the risk-free interest rate in a particular currency, market participants often choose the yield to maturity on a risk-free bond issued by a government of the same currency whose risks of default are so low as to be negligible. For example, the rate of return on T-bills is sometimes seen as the risk-free rate of return in US dollars. Theoretical measurement As stated by Malcolm Kemp in chapter five of his book ''Market Consistency: Model Calibration in Imperfect Markets'', the risk-free rate means different things to different people and there is no consensus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
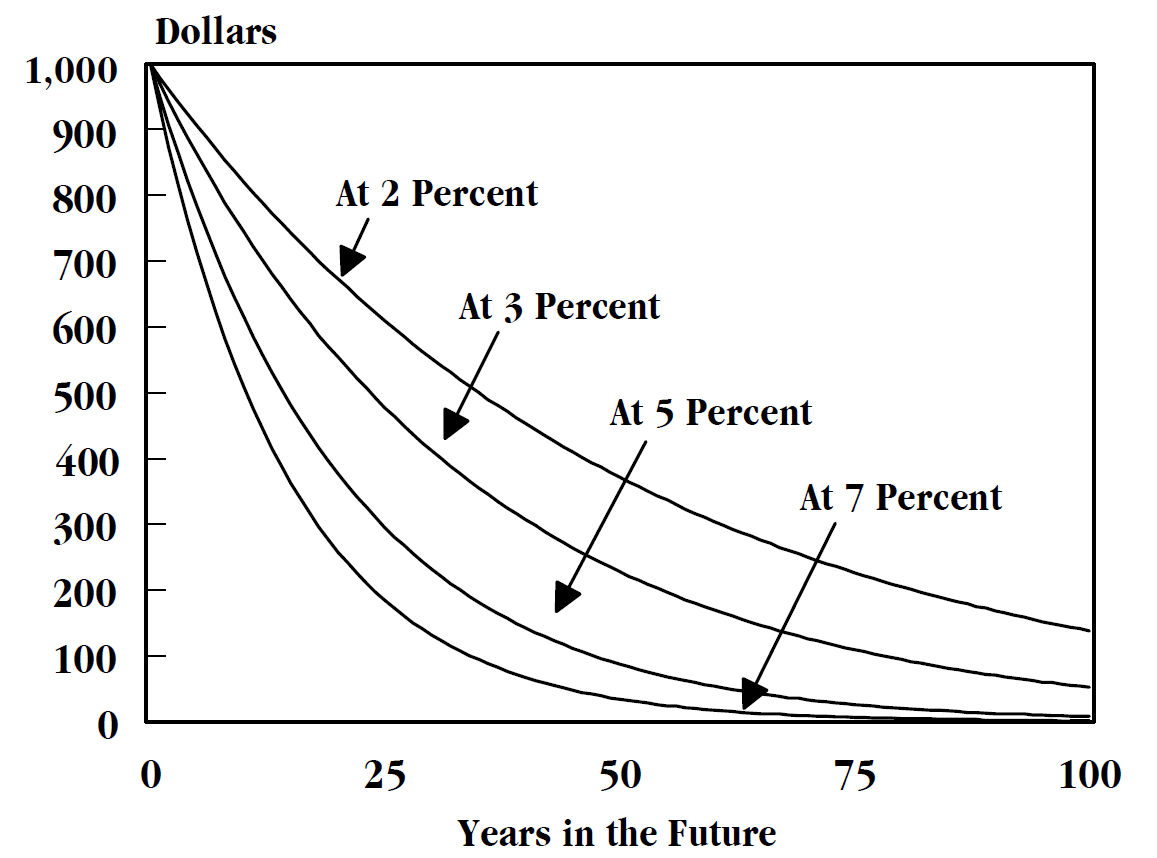
Discounted
Discounting is a financial mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the difference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |