|
Perpendicular And Parallel Unit Vectors
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of ''orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its ''normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
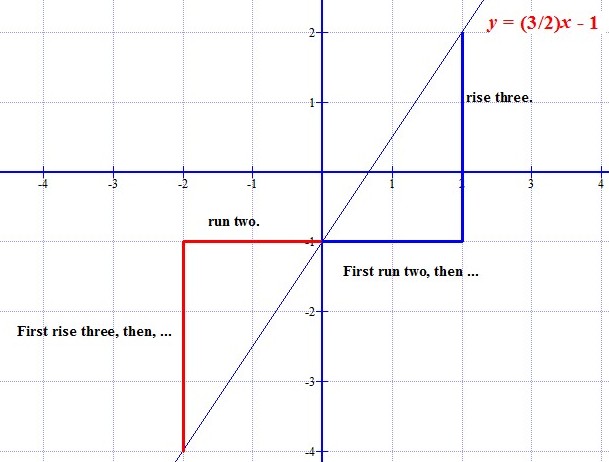
Linear Function
In mathematics, the term linear function refers to two distinct but related notions: * In calculus and related areas, a linear function is a function whose graph is a straight line, that is, a polynomial function of degree zero or one. For distinguishing such a linear function from the other concept, the term ''affine function'' is often used. * In linear algebra, mathematical analysis, and functional analysis, a linear function is a linear map. As a polynomial function In calculus, analytic geometry and related areas, a linear function is a polynomial of degree one or less, including the zero polynomial (the latter not being considered to have degree zero). When the function is of only one variable, it is of the form :f(x)=ax+b, where and are constants, often real numbers. The graph of such a function of one variable is a nonvertical line. is frequently referred to as the slope of the line, and as the intercept. If ''a > 0'' then the gradient is positive an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slopes
In mathematics, the slope or gradient of a Line (mathematics), line is a number that describes the direction (geometry), direction of the line on a plane (geometry), plane. Often denoted by the letter ''m'', slope is calculated as the ratio of the vertical change to the horizontal change ("rise over run") between two distinct points on the line, giving the same number for any choice of points. The line may be physical – as set by a Surveying, road surveyor, pictorial as in a diagram of a road or roof, or Pure mathematics, abstract. An application of the mathematical concept is found in the grade (slope), grade or gradient in geography and civil engineering. The ''steepness'', incline, or grade of a line is the absolute value of its slope: greater absolute value indicates a steeper line. The line trend is defined as follows: *An "increasing" or "ascending" line goes from left to right and has positive slope: m>0. *A "decreasing" or "descending" line goes from left to right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product (mathematics)
In mathematics, a product is the result of multiplication, or an expression that identifies objects (numbers or variables) to be multiplied, called ''factors''. For example, 21 is the product of 3 and 7 (the result of multiplication), and x\cdot (2+x) is the product of x and (2+x) (indicating that the two factors should be multiplied together). When one factor is an integer, the product is called a '' multiple''. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the ''commutative law'' of multiplication. When matrices or members of various other associative algebras are multiplied, the product usually depends on the order of the factors. Matrix multiplication, for example, is non-commutative, and so is multiplication in other algebras in general as well. There are many different kinds of products in mathematics: besides being able to multiply just numbers, polynomials or matrices, one can also define products on many di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slopes And Orthogonality
In mathematics, the slope or gradient of a line is a number that describes the direction of the line on a plane. Often denoted by the letter ''m'', slope is calculated as the ratio of the vertical change to the horizontal change ("rise over run") between two distinct points on the line, giving the same number for any choice of points. The line may be physical – as set by a road surveyor, pictorial as in a diagram of a road or roof, or abstract. An application of the mathematical concept is found in the grade or gradient in geography and civil engineering. The ''steepness'', incline, or grade of a line is the absolute value of its slope: greater absolute value indicates a steeper line. The line trend is defined as follows: *An "increasing" or "ascending" line goes from left to right and has positive slope: m>0. *A "decreasing" or "descending" line goes from left to right and has negative slope: m<0. Special directions are: *A "(square) |
Vertical (angles)
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude or quantity of these types of geometric figures and in this context an angle consists of a number and unit of measurement. Angular measure or measure of angle are sometimes used to distinguish between the measurement and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Postulate
In geometry, the parallel postulate is the fifth postulate in Euclid's ''Elements'' and a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry: If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles. This postulate does not specifically talk about parallel lines; it is only a postulate related to parallelism. Euclid gave the definition of parallel lines in Book I, Definition 23 just before the five postulates. ''Euclidean geometry'' is the study of geometry that satisfies all of Euclid's axioms, including the parallel postulate. The postulate was long considered to be obvious or inevitable, but proofs were elusive. Eventually, it was discovered that inverting the postulate gave valid, albeit different geometries. A geometry where the parallel postulate do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel (geometry)
In geometry, parallel lines are coplanar infinite straight line (geometry), lines that do not intersecting lines, intersect at any point. Parallel planes are plane (geometry), planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not tangent, touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called ''skew lines''. Line segments and Euclidean vectors are parallel if they have the same direction (geometry), direction or opposite direction (geometry), opposite direction (not necessarily the same length). Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometry, affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular Transversal V3
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of ''orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its ''normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |