|
Perifocal Coordinate System
The perifocal coordinate (PQW) system is a frame of reference for an orbit. The frame is centered at the focus of the orbit, i.e. the celestial body about which the orbit is centered. The unit vectors \mathbf and \mathbf lie in the plane of the orbit. \mathbf is directed towards the periapsis of the orbit and \mathbf has a true anomaly (\theta) of 90 degrees past the periapsis. The third unit vector \mathbf is the angular momentum vector and is directed orthogonal to the orbital plane such that: :\mathbf = \mathbf \times \mathbf And, since \mathbf is the angular momentum vector, it may also be expressed as: :\mathbf = \frac where h is the specific relative angular momentum. The position and velocity vectors can be determined for any location of the orbit. The position vector, r, can be expressed as: :\mathbf = \, r\, \cos \theta \mathbf + \, r\, \sin \theta \mathbf where \theta is the true anomaly and the radius ''r'' may be calculated from the orbit equation. The veloc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding of the exact mechanics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Ascension Of The Ascending Node
The longitude of the ascending node (☊ or Ω) is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a specified reference direction, called the ''origin of longitude'', to the direction of the ascending node, as measured in a specified reference plane. The ascending node is the point where the orbit of the object passes through the plane of reference, as seen in the adjacent image. Commonly used reference planes and origins of longitude include: * For geocentric orbits, Earth's equatorial plane as the reference plane, and the First Point of Aries as the origin of longitude. In this case, the longitude is also called the right ascension of the ascending node (RAAN). The angle is measured eastwards (or, as seen from the north, counterclockwise) from the First Point of Aries to the node. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-body Problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored. The most prominent case of the classical two-body problem is the gravitational case (see also Kepler problem), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as satellites, planets, and stars. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions. A simpler "one body" model, the " central-force problem", treats one object as the immobile source of a force acting on the other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much more massive than the other (a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertial Frame Of Reference
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. It is a frame in which an isolated physical object — an object with zero net force acting on it — is perceived to move with a constant velocity (it might be a zero velocity) or, equivalently, it is a frame of reference in which Newton's first law of motion holds. All inertial frames are in a state of constant, rectilinear motion with respect to one another; in other words, an accelerometer moving with any of them would detect zero acceleration. It has been observed that celestial objects which are far away from other objects and which are in uniform motion with respect to the cosmic microwave background radiation maintain such uniform motion. Measurements in one inertial frame can be converted to measurements in another by a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the center of the central mass perpendicular to the plane of motion. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version. Circular acceleration Transverse acceleration (perpendicular to velocity) causes change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle's coordinates with respect to time gives the centripetal acceleration : a\, = \frac \, = where: *v\, is orbital velocity of orbiting body, *r\, is radius of the circ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity Vector
In celestial mechanics, the eccentricity vector of a Kepler orbit is the dimensionless vector with direction pointing from apoapsis to periapsis and with magnitude equal to the orbit's scalar eccentricity. For Kepler orbits the eccentricity vector is a constant of motion. Its main use is in the analysis of almost circular orbits, as perturbing (non-Keplerian) forces on an actual orbit will cause the osculating eccentricity vector to change continuously as opposed to the eccentricity and argument of periapsis parameters for which eccentricity zero (circular orbit) corresponds to a singularity. Calculation The eccentricity vector \mathbf \, is: : \mathbf = - = \left ( - \right ) \mathbf - \mathbf which follows immediately from the vector identity: : \mathbf\times \left ( \mathbf\times \mathbf \right ) = \left ( \mathbf \cdot \mathbf \right ) \mathbf - \left ( \mathbf \cdot \mathbf \right ) \mathbf where: *\mathbf\,\! is position vector *\mathbf\,\! is velocity vector *\m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
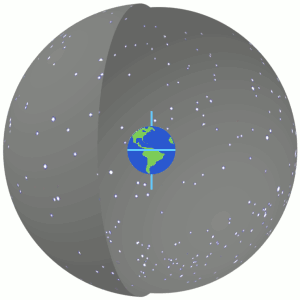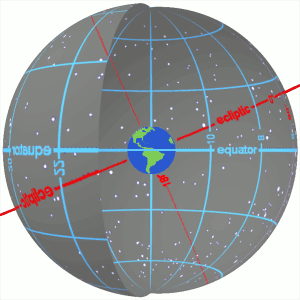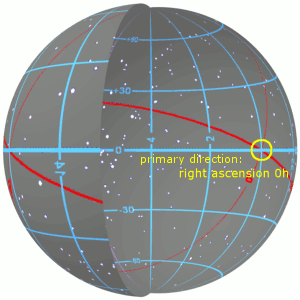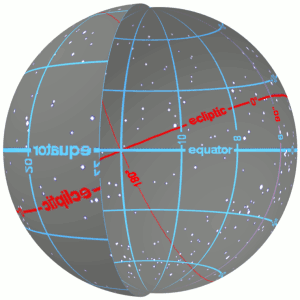
Equatorial Coordinate System
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere (forming the celestial equator), a primary direction towards the vernal equinox, and a right-handed convention. The origin at the centre of Earth means the coordinates are ''geocentric'', that is, as seen from the centre of Earth as if it were transparent. The fundamental plane and the primary direction mean that the coordinate system, while aligned with Earth's equator and pole, does not rotate with the Earth, but remains relatively fixed against the background stars. A right-handed convention means that coordinates increase northward from and eastward around the fundamental plane. Primary direction This description of the orientation of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Argument Of Periapsis
The argument of periapsis (also called argument of perifocus or argument of pericenter), symbolized as ''ω'', is one of the orbital elements of an orbiting body. Parametrically, ''ω'' is the angle from the body's ascending node to its periapsis, measured in the direction of motion. For specific types of orbits, terms such as argument of perihelion (for heliocentric orbits), argument of perigee (for geocentric orbits), argument of periastron (for orbits around stars), and so on, may be used (see apsis for more information). An argument of periapsis of 0° means that the orbiting body will be at its closest approach to the central body at the same moment that it crosses the plane of reference from South to North. An argument of periapsis of 90° means that the orbiting body will reach periapsis at its northmost distance from the plane of reference. Adding the argument of periapsis to the longitude of the ascending node gives the longitude of the periapsis. However, especia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inclination
Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a Plane of reference, reference plane and the orbital plane or Axis of rotation, axis of direction of the orbiting object. For a satellite orbiting the Earth directly above the Equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°. Orbits The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degree (angle), degrees. For a satellite orbiting a planet, the plane of reference is usually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periapsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass is negligible (e.g., f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Mechanics For Engineering Students
''Orbital Mechanics for Engineering Students'' is an aerospace engineering textbook by Howard D. Curtis, in its fourth edition . The book provides an introduction to orbital mechanics, while assuming an undergraduate-level background in physics, rigid body dynamics, differential equations, and linear algebra. Topics covered by the text include a review of kinematics and Newtonian dynamics, the two-body problem, Kepler's laws of planetary motion, orbit determination, orbital maneuvers, relative motion and rendezvous, and interplanetary trajectories. The text focuses primarily on orbital mechanics, but also includes material on rigid body dynamics, rocket vehicle dynamics, and attitude control. Control theory and spacecraft control systems are less thoroughly covered. The textbook includes exercises at the end of each chapter, and supplemental material is available online, including MATLAB MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-parad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * circular orbit: ''e'' = 0 * elliptic orbit: 0 < ''e'' < 1 * |


.png)