|
Pauli Group
In physics and mathematics, the Pauli group is a 16-element matrix group Matrix group The Pauli group consists of the 2 × 2 identity matrix I and all of the Pauli matrices :X = \sigma_1 = \begin 0&1\\ 1&0 \end,\quad Y = \sigma_2 = \begin 0&-i\\ i&0 \end,\quad Z = \sigma_3 = \begin 1&0\\ 0&-1 \end, together with the products of these matrices with the factors \pm 1 and \pm i: :G \ \stackrel\ \ \equiv \langle X, Y, Z \rangle. The Pauli group is Generating_set_of_a_group, generated by the Pauli matrices, and like them it is named after Wolfgang Pauli. As an abstract group, G \ \cong C_4 \circ D_4 is the central product of a cyclic group of order 4 and the dihedral group of order 8. The Pauli group is a group representation, representation of the Higher-dimensional gamma matrices, gamma group in three-dimensional Euclidean space. It is ''not'' isomorphic to the gamma group; it is less free, in that its chiral element is \sigma_1\sigma_2\sigma_3=iI whereas there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cayley Graph Pauli
Cayley may refer to: __NOTOC__ People * Cayley (surname) * Cayley Illingworth (1759–1823), Anglican Archdeacon of Stow * Cayley Mercer (born 1994), Canadian women's ice hockey player Places * Cayley, Alberta, Canada, a hamlet ** Cayley/A. J. Flying Ranch Airport * Mount Cayley, a volcano in southwestern British Columbia, Canada * Cayley Glacier, Graham Land, Antarctica * Cayley (crater), a lunar crater Other uses * Cayley baronets, a title in the Baronetage of England * Cayley computer algebra system, designed to solve mathematical problems, particularly in group theory See also * W. Cayley Hamilton (died 1891), Canadian barrister and politician * Caylee (name), given name * Cèilidh, traditional Scottish or Irish social gathering * Kaylee, given name * Kaley (other) Kaley may refer to: * Kaley Cuoco Kaley Christine Cuoco ( ; born November 30, 1985) is an American actress. She starred as Bridget Hennessy on the ABC sitcom '' 8 Simple Rules'' (2002–2005 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Multiplication
In mathematics, specifically in linear algebra, matrix multiplication is a binary operation that produces a matrix (mathematics), matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices and is denoted as . Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812, to represent the composition of functions, composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra. Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New York City
New York, often called New York City (NYC), is the most populous city in the United States, located at the southern tip of New York State on one of the world's largest natural harbors. The city comprises five boroughs, each coextensive with a respective county. The city is the geographical and demographic center of both the Northeast megalopolis and the New York metropolitan area, the largest metropolitan area in the United States by both population and urban area. New York is a global center of finance and commerce, culture, technology, entertainment and media, academics, and scientific output, the arts and fashion, and, as home to the headquarters of the United Nations, international diplomacy. With an estimated population in 2024 of 8,478,072 distributed over , the city is the most densely populated major city in the United States. New York City has more than double the population of Los Angeles, the nation's second-most populous city. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
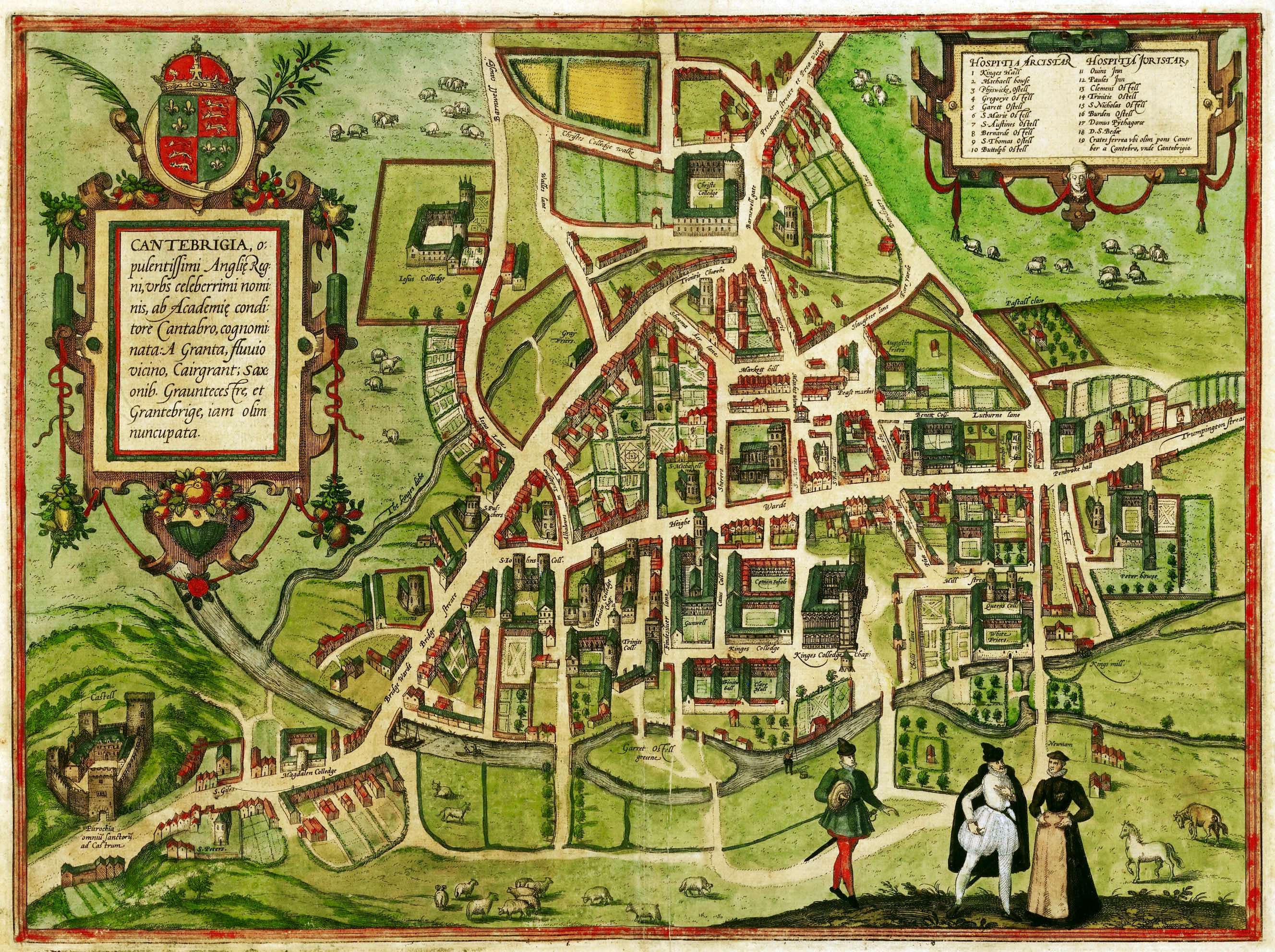
Cambridge
Cambridge ( ) is a List of cities in the United Kingdom, city and non-metropolitan district in the county of Cambridgeshire, England. It is the county town of Cambridgeshire and is located on the River Cam, north of London. As of the 2021 United Kingdom census, the population of the City of Cambridge was 145,700; the population of the wider built-up area (which extends outside the city council area) was 181,137. (2021 census) There is archaeological evidence of settlement in the area as early as the Bronze Age, and Cambridge became an important trading centre during the Roman Britain, Roman and Viking eras. The first Town charter#Municipal charters, town charters were granted in the 12th century, although modern city status was not officially conferred until 1951. The city is well known as the home of the University of Cambridge, which was founded in 1209 and consistently ranks among the best universities in the world. The buildings of the university include King's College Chap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computation And Quantum Information (book)
''Quantum Computation and Quantum Information'' is a textbook about quantum information science written by Michael Nielsen and Isaac Chuang, regarded as a standard text on the subject. It is informally known as "Mike and Ike", after the candies of that name. The book assumes minimal prior experience with quantum mechanics and with computer science, aiming instead to be a self-contained introduction to the relevant features of both. ( Lov Grover recalls a postdoc disparaging it with the remark, "The book is too elementary – it starts off with the assumption that the reader does not even know quantum mechanics.") The focus of the text is on theory, rather than the experimental implementations of quantum computers, which are discussed more briefly. , the book has been cited over 58,000 times on Google Scholar. In 2019, Nielsen adapted parts of the book for his ''Quantum Country'' project. Table of Contents (Tenth Anniversary Edition) * Chapter 1: Introduction and Over ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order (group Theory)
In mathematics, the order of a finite group is the number of its elements. If a group is not finite, one says that its order is ''infinite''. The ''order'' of an element of a group (also called period length or period) is the order of the subgroup generated by the element. If the group operation is denoted as a multiplication, the order of an element of a group, is thus the smallest positive integer such that , where denotes the identity element of the group, and denotes the product of copies of . If no such exists, the order of is infinite. The order of a group is denoted by or , and the order of an element is denoted by or , instead of \operatorname(\langle a\rangle), where the brackets denote the generated group. Lagrange's theorem states that for any subgroup of a finite group , the order of the subgroup divides the order of the group; that is, is a divisor of . In particular, the order of any element is a divisor of . Example The symmetric group S3 ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product
In mathematics, the tensor product V \otimes W of two vector spaces V and W (over the same field) is a vector space to which is associated a bilinear map V\times W \rightarrow V\otimes W that maps a pair (v,w),\ v\in V, w\in W to an element of V \otimes W denoted . An element of the form v \otimes w is called the tensor product of v and w. An element of V \otimes W is a tensor, and the tensor product of two vectors is sometimes called an ''elementary tensor'' or a ''decomposable tensor''. The elementary tensors span V \otimes W in the sense that every element of V \otimes W is a sum of elementary tensors. If bases are given for V and W, a basis of V \otimes W is formed by all tensor products of a basis element of V and a basis element of W. The tensor product of two vector spaces captures the properties of all bilinear maps in the sense that a bilinear map from V\times W into another vector space Z factors uniquely through a linear map V\otimes W\to Z (see the section below ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Qubit
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical system, one of the simplest quantum systems displaying the peculiarity of quantum mechanics. Examples include the spin of the electron in which the two levels can be taken as spin up and spin down; or the polarization of a single photon in which the two spin states (left-handed and the right-handed circular polarization) can also be measured as horizontal and vertical linear polarization. In a classical system, a bit would have to be in one state or the other. However, quantum mechanics allows the qubit to be in a coherent superposition of multiple states simultaneously, a property that is fundamental to quantum mechanics and quantum computing. Etymology The coining of the term ''qubit'' is attributed to Benjamin Schumacher. In the acknow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis (linear Algebra)
In mathematics, a Set (mathematics), set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension (vector space), dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frame of reference, frames of reference. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eponym
An eponym is a noun after which or for which someone or something is, or is believed to be, named. Adjectives derived from the word ''eponym'' include ''eponymous'' and ''eponymic''. Eponyms are commonly used for time periods, places, innovations, biological nomenclature, astronomical objects, works of art and media, and tribal names. Various orthographic conventions are used for eponyms. Usage of the word The term ''eponym'' functions in multiple related ways, all based on an explicit relationship between two named things. ''Eponym'' may refer to a person or, less commonly, a place or thing for which someone or something is, or is believed to be, named. ''Eponym'' may also refer to someone or something named after, or believed to be named after, a person or, less commonly, a place or thing. A person, place, or thing named after a particular person share an eponymous relationship. In this way, Elizabeth I of England is the eponym of the Elizabethan era, but the Elizabethan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |