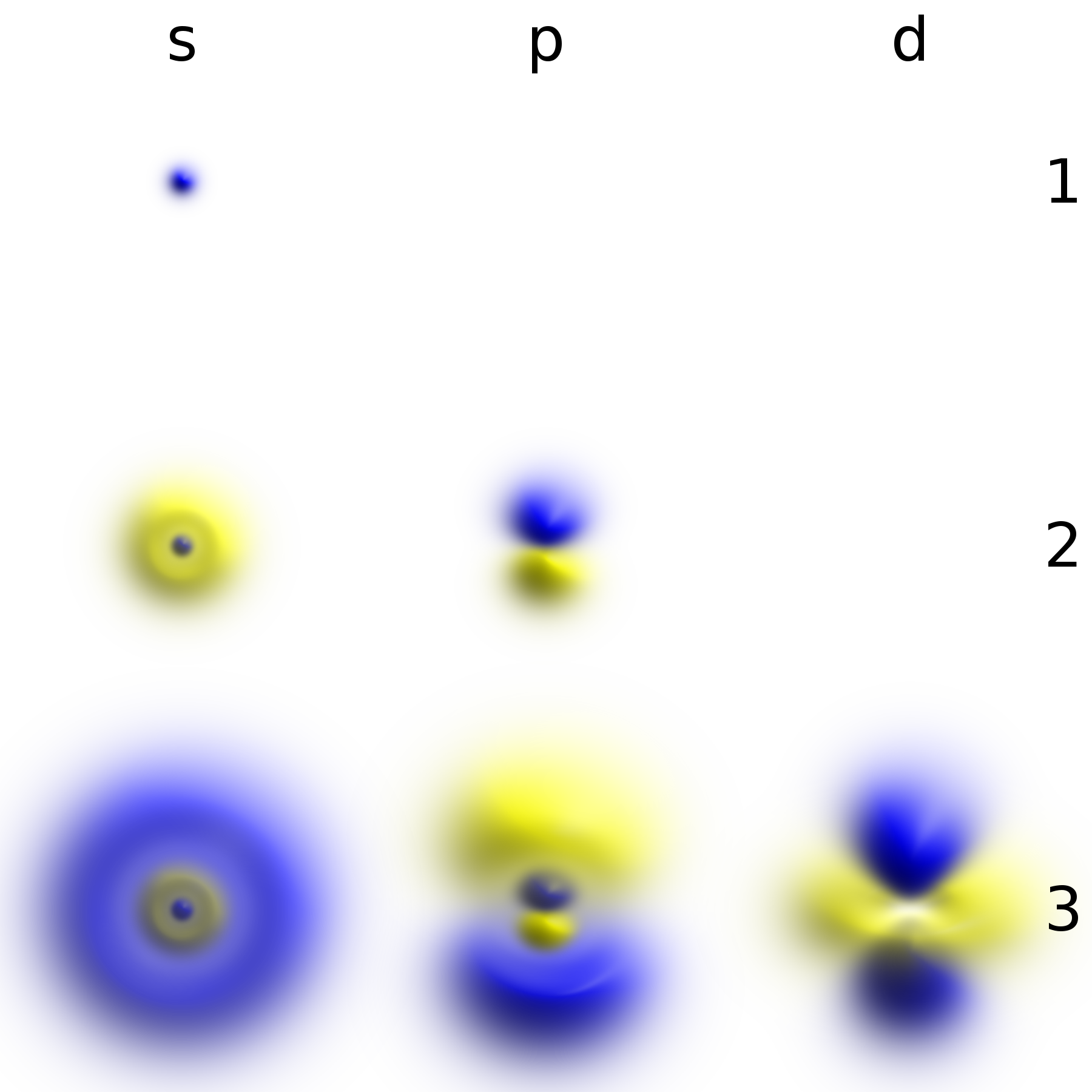
|
POVM
In functional analysis and quantum information science, a positive operator-valued measure (POVM) is a measure whose values are positive semi-definite operators on a Hilbert space. POVMs are a generalization of projection-valued measures (PVM) and, correspondingly, quantum measurements described by POVMs are a generalization of quantum measurement described by PVMs (called projective measurements). In rough analogy, a POVM is to a PVM what a mixed state is to a pure state. Mixed states are needed to specify the state of a subsystem of a larger system (see purification of quantum state); analogously, POVMs are necessary to describe the effect on a subsystem of a projective measurement performed on a larger system. POVMs are the most general kind of measurement in quantum mechanics, and can also be used in quantum field theory. They are extensively used in the field of quantum information. Definition Let \mathcal denote a Hilbert space and (X, M) a measurable space with M a B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (e.g. inner product, norm, topology, etc.) and the linear functions defined on these spaces and respecting these structures in a suitable sense. The historical roots of functional analysis lie in the study of spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining continuous, unitary etc. operators between function spaces. This point of view turned out to be particularly useful for the study of differential and integral equations. The usage of the word '' functional'' as a noun goes back to the calculus of variations, implying a function whose argument is a function. The term was first used in Hadamard's 1910 book on that subject. However, the general concept of a functional had previously been introduced in 1887 by the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Operator
Identity may refer to: * Identity document * Identity (philosophy) * Identity (social science) * Identity (mathematics) Arts and entertainment Film and television * ''Identity'' (1987 film), an Iranian film * ''Identity'' (2003 film), an American slasher film * ''Identity'' (game show), an American game show * ''Identity'' (TV series), a British police procedural drama television series * "Identity" (''Arrow''), a 2013 episode * "Identity" (''Burn Notice''), a 2007 episode * "Identity" (''Charlie Jade''), a 2005 episode * "Identity" (''Legend of the Seeker''), a 2008 episode * "Identity" (''Law & Order: Special Victims Unit'' episode), 2005 * "Identity" (''NCIS: Los Angeles''), a 2009 pilot episode Music Albums * ''Identity'' (3T album), 2004 * ''Identity'' (BoA album), 2010 * ''Identity'' (Far East Movement album), 2016 * ''Identity'' (Robert Pierre album), 2008 * ''Identity'' (Raghav album), 2008 * ''Identity'' (Victon EP), 2017 * ''Identity'' (Zee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Coin Flipping
Consider two remote players, connected by a channel, that don't trust each other. The problem of them agreeing on a random bit by exchanging messages over this channel, without relying on any trusted third party, is called the coin flipping problem in cryptography. Quantum coin flipping uses the principles of quantum mechanics to encrypt messages for secure communication. It is a cryptographic primitive which can be used to construct more complex and useful cryptographic protocols, e.g. Quantum Byzantine agreement. Unlike other types of quantum cryptography (in particular, quantum key distribution), quantum coin flipping is a protocol used between two users who do not trust each other.Stuart Mason Dambort"Heads or tails: Experimental quantum coin flipping cryptography performs better than classical protocols" ''Phys.org'', March 26, 2014 Consequently, both users (or players) want to win the coin toss and will attempt to cheat in various ways. It is known that if the communication be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Cryptography
Quantum cryptography is the science of exploiting quantum mechanical properties to perform cryptographic tasks. The best known example of quantum cryptography is quantum key distribution which offers an information-theoretically secure solution to the key exchange problem. The advantage of quantum cryptography lies in the fact that it allows the completion of various cryptographic tasks that are proven or conjectured to be impossible using only classical (i.e. non-quantum) communication. For example, it is impossible to copy data encoded in a quantum state. If one attempts to read the encoded data, the quantum state will be changed due to wave function collapse (no-cloning theorem). This could be used to detect eavesdropping in quantum key distribution (QKD). History In the early 1970s, Stephen Wiesner, then at Columbia University in New York, introduced the concept of quantum conjugate coding. His seminal paper titled "Conjugate Coding" was rejected by the IEEE Informati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bloch Sphere Representation Of Optimal POVM And States For Unambiguous Quantum State Discrimination
Bloch is a surname of German origin. Notable people with this surname include: A–F * (1859-1914), French rabbi *Adele Bloch-Bauer (1881-1925), Austrian entrepreneur *Albert Bloch (1882–1961), American painter * (born 1972), German motor journalist and presenter * (1878–?), Russian lawyer, journalist, lawyer, and revolutionary *Alexandre Bloch (1857–1919), French painter *Alfred Bloch (born 1877), French footballer * (1915–1983), Swiss linguist * (1904–1979), German-British engineer *Aliza Bloch (born 1957), First female mayor of Bet Shemesh, Israel * (1768–1838), Swiss Benedictine monk *André Bloch (composer) (1873–1960), French composer and music educator *André Bloch (mathematician) (1893–1948), French mathematician * (1914–1942), French agent of the Special Operations Executive *Andreas Bloch (1860–1917), Norwegian painter, illustrator and costume designer *Andy Bloch (born 1969), American poker player *Anna Bloch (1868–1953), Danish actress *Armand Blo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' meaning "equal", and μέτρον ''metron'' meaning "measure". Introduction Given a metric space (loosely, a set and a scheme for assigning distances between elements of the set), an isometry is a transformation which maps elements to the same or another metric space such that the distance between the image elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional Euclidean space, two geometric figures are congruent if they are related by an isometry; the isometry that relates them is either a rigid motion (translation or rotation), or a composition of a rigid motion and a reflection. Isometries are often used in constructions where one spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Naimark's Dilation Theorem
In operator theory, Naimark's dilation theorem is a result that characterizes positive operator valued measures. It can be viewed as a consequence of Stinespring's dilation theorem. Some preliminary notions Let ''X'' be a compact Hausdorff space, ''H'' be a Hilbert space, and ''L(H)'' the Banach space of bounded operators on ''H''. A mapping ''E'' from the Borel σ-algebra on ''X'' to L(H) is called an operator-valued measure if it is weakly countably additive, that is, for any disjoint sequence of Borel sets \, we have : \langle E (\cup _i B_i) x, y \rangle = \sum_i \langle E (B_i) x, y \rangle for all ''x'' and ''y''. Some terminology for describing such measures are: * ''E'' is called ''regular'' if the scalar valued measure : B \rightarrow \langle E (B) x, y \rangle is a regular Borel measure, meaning all compact sets have finite total variation and the measure of a set can be approximated by those of open sets. * ''E'' is called ''bounded'' if , E, = \sup_B \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (linear Algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix (). It can be proved that the trace of a matrix is the sum of its (complex) eigenvalues (counted with multiplicities). It can also be proved that for any two matrices and . This implies that similar matrices have the same trace. As a consequence one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the th row and th column of . The entries of can be real numbers or (more generally) complex numbers. The trace is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Measurement
In quantum physics, a measurement is the testing or manipulation of a physical system to yield a numerical result. The predictions that quantum physics makes are in general probabilistic. The mathematical tools for making predictions about what measurement outcomes may occur were developed during the 20th century and make use of linear algebra and functional analysis. Quantum physics has proven to be an empirical success and to have wide-ranging applicability. However, on a more philosophical level, debates continue about the meaning of the measurement concept. Mathematical formalism "Observables" as self-adjoint operators In quantum mechanics, each physical system is associated with a Hilbert space, each element of which represents a possible state of the physical system. The approach codified by John von Neumann represents a measurement upon a physical system by a self-adjoint operator on that Hilbert space termed an "observable". These observables play the role of measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum State
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers, while mixed states are represented by density matrices, which are positive semidefinite operators that act on Hilbert spaces. Pure states are also known as state vectors or wave functions, the latter term applying particularly when they are represented as functions of position or momentum. For example, when dealing with the energy spectrum of the electron in a hydrogen a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |