|
Oval (projective Plane)
In projective geometry an oval is a point set in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics. As mentioned, in projective geometry an oval is defined by incidence properties, but in other areas, ovals may be defined to satisfy other criteria, for instance, in differential geometry by differentiability conditions in the real plane. The higher dimensional analog of an oval is an ovoid in a projective space. A generalization of the oval concept is an abstract oval, which is a structure that is not necessarily embedded in a projective plane. Indeed, there exist abstract ovals which can not lie in any projective plane. Definition of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projectivity
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation. Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ''homography'', which, etymologically, roughly means "similar drawing", dates from this time. At the end of the 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term "projective transformation" originated in these abstr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Quadrangle
In geometry, a generalized quadrangle is an incidence structure whose main feature is the lack of any triangles (yet containing many quadrangles). A generalized quadrangle is by definition a polar space of rank two. They are the with ''n'' = 4 and near 2n-gons with ''n'' = 2. They are also precisely the partial geometries pg(''s'',''t'',α) with α = 1. Definition A generalized quadrangle is an incidence structure (''P'',''B'',I), with I ⊆ ''P'' × ''B'' an incidence relation, satisfying certain axioms. Elements of ''P'' are by definition the ''points'' of the generalized quadrangle, elements of ''B'' the ''lines''. The axioms are the following: * There is an ''s'' (''s'' ≥ 1) such that on every line there are exactly ''s'' + 1 points. There is at most one point on two distinct lines. * There is a ''t'' (''t'' ≥ 1) such that through every point there are exactly ''t'' + 1 lines. There is at most one line through two distinct points. * For every point ''p'' not on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
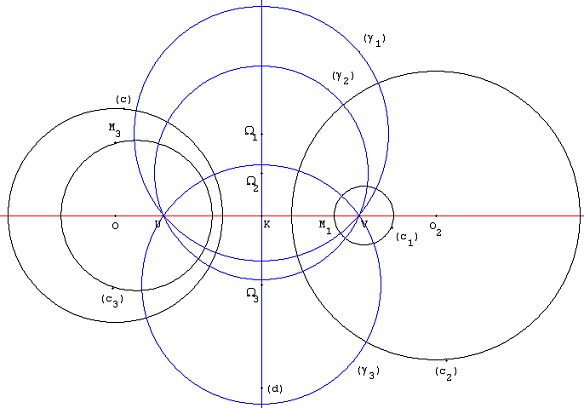
Arc (projective Geometry)
An (''simple'') arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of ''curved'' figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called -arcs. An important generalization of the -arc concept, also referred to as arcs in the literature, are the ()-arcs. -arcs in a projective plane In a finite projective plane (not necessarily Desarguesian) a set of points such that no three points of are collinear (on a line) is called a . If the plane has order then , however the maximum value of can only be achieved if is even. In a plane of order , a -arc is called an oval and, if is even, a -arc is called a hyperoval. Every conic in the Desarguesian projective plane PG(2,), i.e., the set of zero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation Polynomial
In mathematics, a permutation polynomial (for a given ring) is a polynomial that acts as a permutation of the elements of the ring, i.e. the map x \mapsto g(x) is a bijection. In case the ring is a finite field, the Dickson polynomials, which are closely related to the Chebyshev polynomials, provide examples. Over a finite field, every function, so in particular every permutation of the elements of that field, can be written as a polynomial function. In the case of finite rings Z/''n''Z, such polynomials have also been studied and applied in the interleaver component of error detection and correction algorithms. Single variable permutation polynomials over finite fields Let be the finite field of characteristic , that is, the field having elements where for some prime . A polynomial with coefficients in (symbolically written as ) is a ''permutation polynomial'' of if the function from to itself defined by c \mapsto f(c) is a permutation of . Due to the finiteness ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximal Arc
A Maximal arc in a finite projective plane In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that d ... is a largest possible (''k'',''d'')- arc in that projective plane. If the finite projective plane has order ''q'' (there are ''q''+1 points on any line), then for a maximal arc, ''k'', the number of points of the arc, is the maximum possible (= ''qd'' + ''d'' - ''q'') with the property that no ''d''+1 points of the arc lie on the same line. Definition Let \pi be a finite projective plane of order ''q'' (not necessarily desarguesian). Maximal arcs of ''degree'' ''d'' ( 2 ≤ ''d'' ≤ ''q''- 1) are (''k'',''d'')- arcs in \pi, where ''k'' is maximal with respect to the parameter ''d'', in other words, ''k'' = ''qd'' + ''d'' - ''q''. Equivalently, one can define maximal arcs of degree ''d'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperoval In Fano Plane
In projective geometry an oval is a point set in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics. As mentioned, in projective geometry an oval is defined by incidence properties, but in other areas, ovals may be defined to satisfy other criteria, for instance, in differential geometry by differentiability conditions in the real plane. The higher dimensional analog of an oval is an ovoid in a projective space. A generalization of the oval concept is an abstract oval, which is a structure that is not necessarily embedded in a projective plane. Indeed, there exist abstract ovals which can not lie in any projective plane. Definition of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Qvist's Theorem
In projective geometry, Qvist's theorem, named after the Finnish mathematician , is a statement on ovals in ''finite'' projective planes. Standard examples of ovals are non-degenerate (projective) conic sections. The theorem gives an answer to the question ''How many tangents to an oval can pass through a point in a finite projective plane?'' The answer depends essentially upon the order (number of points on a line −1) of the plane. Definition of an oval *In a projective plane a set of points is called an oval, if: # Any line meets in at most two points, and # For any point there exists exactly one tangent line through , i.e., . When the line is an ''exterior line'' (or ''passant''), if a ''tangent line'' and if the line is a ''secant line''. For ''finite'' planes (i.e. the set of points is finite) we have a more convenient characterization: * For a finite projective plane of ''order'' (i.e. any line contains points) a set of points is an oval if and only if and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Desarguesian Plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus ''any'' two distinct lines in a projective plane intersect at exactly one point. Renaissance artists, in developing the techniques of drawing in perspective, laid the groundwork for this mathematical topic. The archetypical example is the real projective plane, also known as the extended Euclidean plane. This example, in slightly different guises, is important in algebraic geometry, topology and projective geometry where it may be denoted variously by , RP2, or P2(R), among other notations. There are many other projective planes, both infinite, such as the complex projective plane, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc (projective Geometry)
An (''simple'') arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of ''curved'' figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called -arcs. An important generalization of the -arc concept, also referred to as arcs in the literature, are the ()-arcs. -arcs in a projective plane In a finite projective plane (not necessarily Desarguesian) a set of points such that no three points of are collinear (on a line) is called a . If the plane has order then , however the maximum value of can only be achieved if is even. In a plane of order , a -arc is called an oval and, if is even, a -arc is called a hyperoval. Every conic in the Desarguesian projective plane PG(2,), i.e., the set of zero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Segre's Theorem
In projective geometry, Segre's theorem, named after the Italian mathematician Beniamino Segre, is the statement: *Any oval in a ''finite pappian'' projective plane of ''odd'' order is a nondegenerate projective conic section. This statement was assumed 1949 by the two Finnish mathematicians G. Järnefelt and P. Kustaanheimo and its proof was published in 1955 by B. Segre. A finite pappian projective plane can be imagined as the projective closure of the real plane (by a line at infinity), where the real numbers are replaced by a finite field . ''Odd order'' means that is odd. An oval is a curve similar to a circle (see definition below): any line meets it in at most 2 points and through any point of it there is exactly one tangent. The standard examples are the nondegenerate projective conic sections. In pappian projective planes of ''even'' order greater than four there are ovals which are not conics. In an infinite plane there exist ovals, which are not conics. In the real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspectivity
In geometry and in its applications to drawing, a perspectivity is the formation of an image in a picture plane of a scene viewed from a fixed point. Graphics The science of graphical perspective uses perspectivities to make realistic images in proper proportion. According to Kirsti Andersen, the first author to describe perspectivity was Leon Alberti in his ''De Pictura'' (1435). In English, Brook Taylor presented his ''Linear Perspective'' in 1715, where he explained "Perspective is the Art of drawing on a Plane the Appearances of any Figures, by the Rules of Geometry". In a second book, ''New Principles of Linear Perspective'' (1719), Taylor wrote :When Lines drawn according to a certain Law from the several Parts of any Figure, cut a Plane, and by that Cutting or Intersection describe a figure on that Plane, that Figure so described is called the ''Projection'' of the other Figure. The Lines producing that Projection, taken all together, are called the ''System of Rays''. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |