|
Nonlinear Filter
In signal processing, a nonlinear filter is a filter whose output is not a linear function of its input. That is, if the filter outputs signals and for two input signals and separately, but does not always output when the input is a linear combination . Both continuous-domain and discrete-domain filters may be nonlinear. A simple example of the former would be an electrical device whose output voltage at any moment is the square of the input voltage ; or which is the input clipped to a fixed range , namely . An important example of the latter is the running-median filter, such that every output sample is the median of the last three input samples . Like linear filters, nonlinear filters may be shift invariant or not. Non-linear filters have many applications, especially in the removal of certain types of noise that are not additive. For example, the median filter is widely used to remove spike noise — that affects only a small percentage of the samples, possibly b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
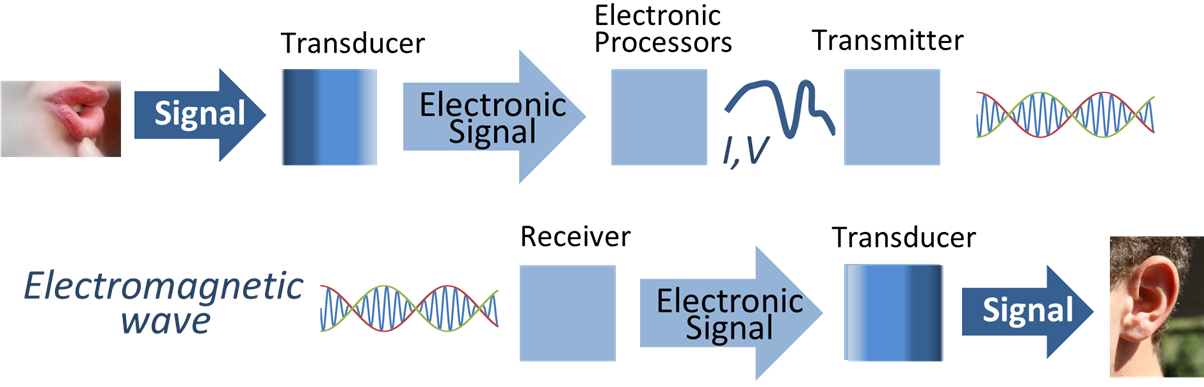
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analog-to-digital Converter
In electronics, an analog-to-digital converter (ADC, A/D, or A-to-D) is a system that converts an analog signal, such as a sound picked up by a microphone or light entering a digital camera, into a Digital signal (signal processing), digital signal. An ADC may also provide an isolated measurement such as an electronic device that converts an analog input voltage or Electric current, current to a digital number representing the magnitude of the voltage or current. Typically the digital output is a two's complement binary number that is proportional to the input, but there are other possibilities. There are several ADC hardware architecture, architectures. Due to the complexity and the need for precisely matched electronic component, components, all but the most specialized ADCs are implemented as integrated circuits (ICs). These typically take the form of metal–oxide–semiconductor (MOS) mixed-signal integrated circuit chips that integrate both Analogue electronics, anal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Noise
In signal processing, the term multiplicative noise refers to an unwanted random signal that gets multiplied into some relevant signal during capture, transmission, or other processing. Multiplicative noise is a type of signal-dependent noise where the noise amplitude scales with the signal's intensity. Unlike additive noise, which is independent of the signal, multiplicative noise complicates processing due to its dependence on the underlying signal. An important example is the speckle noise commonly observed in radar imagery. Examples of multiplicative noise affecting digital photographs are proper shadows due to undulations on the surface of the imaged objects, shadows cast by complex objects like foliage and Venetian blinds, dark spots caused by dust in the lens or image sensor, and variations in the gain of individual elements of the image sensor array. Maria Petrou, Costas Petrou (2010Image Processing: The Fundamentals John Wiley & Sons. 818 pages. Multiplicative No ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bandpass Filter
A band-pass filter or bandpass filter (BPF) is a device that passes frequencies within a certain range and rejects ( attenuates) frequencies outside that range. It is the inverse of a '' band-stop filter''. Description In electronics and signal processing, a filter is usually a two-port circuit or device which removes frequency components of a signal (an alternating voltage or current). A band-pass filter allows through components in a specified band of frequencies, called its '' passband'' but blocks components with frequencies above or below this band. This contrasts with a high-pass filter, which allows through components with frequencies above a specific frequency, and a low-pass filter, which allows through components with frequencies below a specific frequency. In digital signal processing, in which signals represented by digital numbers are processed by computer programs, a band-pass filter is a computer algorithm that performs the same function. The term ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Domain
In mathematics, physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency (and possibly phase), rather than time, as in time series. While a time-domain graph shows how a signal changes over time, a frequency-domain graph shows how the signal is distributed within different frequency bands over a range of frequencies. A complex valued frequency-domain representation consists of both the magnitude and the phase of a set of sinusoids (or other basis waveforms) at the frequency components of the signal. Although it is common to refer to the magnitude portion (the real valued frequency-domain) as the frequency response of a signal, the phase portion is required to uniquely define the signal. A given function or signal can be converted between the time and frequency domains with a pair of mathematical operators called transforms. An example is the Fourier transfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shannon's Theorem
In information theory, the noisy-channel coding theorem (sometimes Shannon's theorem or Shannon's limit), establishes that for any given degree of noise contamination of a communication channel, it is possible (in theory) to communicate discrete data (digital information) nearly error-free up to a computable maximum rate through the channel. This result was presented by Claude Shannon in 1948 and was based in part on earlier work and ideas of Harry Nyquist and Ralph Hartley. The Shannon limit or Shannon capacity of a communication channel refers to the maximum Code rate, rate of error-free data that can theoretically be transferred over the channel if the link is subject to random data transmission errors, for a particular noise level. It was first described by Shannon (1948), and shortly after published in a book by Shannon and Warren Weaver entitled ''The Mathematical Theory of Communication'' (1949). This founded the modern discipline of information theory. Overview State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kalman Filter
In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unknown variables that tend to be more accurate than those based on a single measurement, by estimating a joint probability distribution over the variables for each time-step. The filter is constructed as a mean squared error minimiser, but an alternative derivation of the filter is also provided showing how the filter relates to maximum likelihood statistics. The filter is named after Rudolf E. Kálmán. Kalman filtering has numerous technological applications. A common application is for guidance, navigation, and control of vehicles, particularly aircraft, spacecraft and ships Dynamic positioning, positioned dynamically. Furthermore, Kalman filtering is much applied in time series analysis tasks such as signal processing and econometrics. K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Noise
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below. There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymous adjective ''Gaussian'' is pronounced . Mathematics Algebra and linear algebra Geometry and differential geometry Number theory Cyclotomic fields *Gaussian period *Gaussian rational *Gauss sum, an exponential sum over Dirichlet characters **Elliptic Gauss sum, an analog of a Gauss sum **Quadratic Gauss sum Analysis, numerical analysis, vector calculus and calculus of variations Complex analysis and convex analysis *Gauss–Lucas theorem *Gauss's continued fraction, an analytic continued fraction derived from the hypergeometric functions *Gauss's test, Gauss's criterion – described oEncyclopedia of Mathematics*Gauss's hypergeometric theorem, an identity on hypergeometric series *Gauss plane Statistics *Gaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar (mathematics)
A scalar is an element of a field which is used to define a ''vector space''. In linear algebra, real numbers or generally elements of a field are called scalars and relate to vectors in an associated vector space through the operation of scalar multiplication (defined in the vector space), in which a vector can be multiplied by a scalar in the defined way to produce another vector. Generally speaking, a vector space may be defined by using any field instead of real numbers (such as complex numbers). Then scalars of that vector space will be elements of the associated field (such as complex numbers). A scalar product operation – not to be confused with scalar multiplication – may be defined on a vector space, allowing two vectors to be multiplied in the defined way to produce a scalar. A vector space equipped with a scalar product is called an inner product space. A quantity described by multiple scalars, such as having both direction and magnitude, is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearity
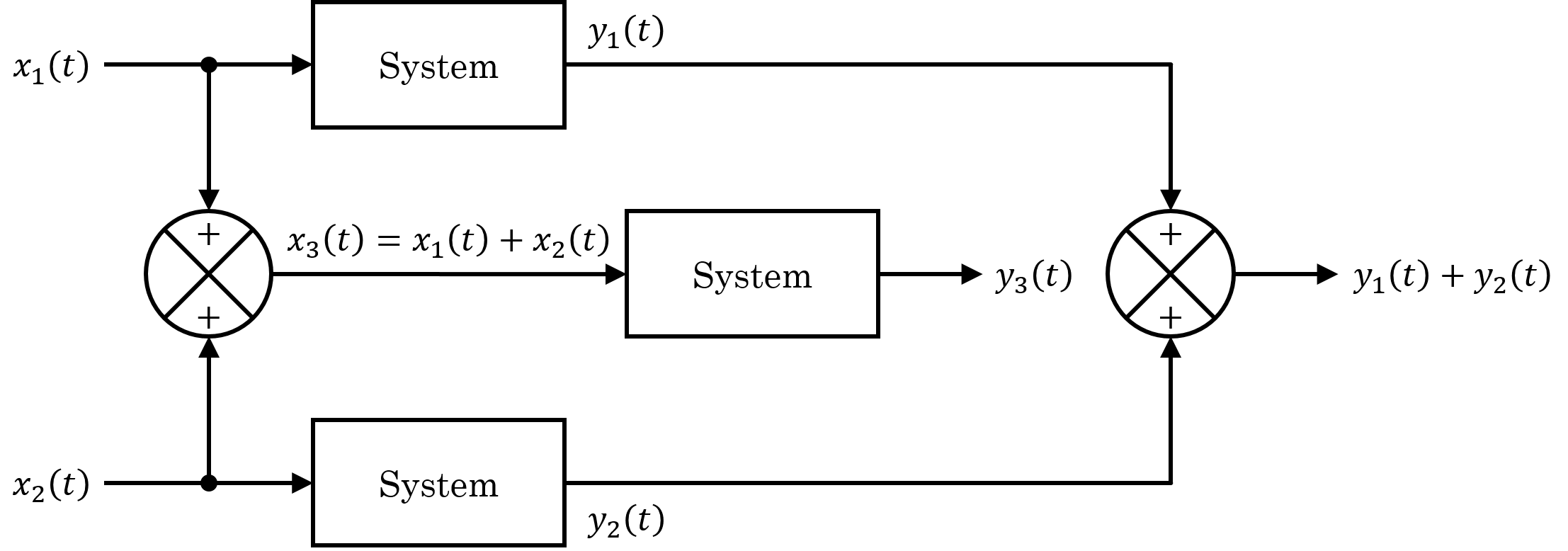
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a '' polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are '' nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Response
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and Phase (waves), phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio system, audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, Audio power amplifier, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's Bandwidth (signal processing), bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system Stability theory, stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog filter, analog and digital filters. The frequency ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |