|
Moneyness
In finance, moneyness is the relative position of the current price (or future price) of an underlying asset (e.g., a stock) with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a three-fold classification: * If the derivative would have positive intrinsic value if it were to expire today, it is said to be in the money (ITM); * If the derivative would be worthless if expiring with the underlying at its current price, it is said to be out of the money (OTM); * And if the current underlying price and strike price are equal, the derivative is said to be at the money (ATM). There are two slightly different definitions, according to whether one uses the current price (spot) or future price (forward), specified as "at the money spot" or "at the money forward", etc. This rough classification can be quantified by various definitions to express the moneyness as a number, measuring how far the asset is in the money or out o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strike Price
In finance, the strike price (or exercise price) of an option is a fixed price at which the owner of the option can buy (in the case of a call), or sell (in the case of a put), the underlying security or commodity. The strike price may be set by reference to the spot price, which is the market price of the underlying security or commodity on the day an option is taken out. Alternatively, the strike price may be fixed at a discount or premium. The strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the market price of the underlying instrument at that time. Moneyness Moneyness is the value of a financial contract if the contract settlement is financial. More specifically, it is the difference between the strike price of the option and the current trading price of its underlying security. In options trading, terms such as ''in-the- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility Surface
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Call Option
In finance, a call option, often simply labeled a "call", is a contract between the buyer and the seller of the call Option (finance), option to exchange a Security (finance), security at a set price. The buyer of the call option has the right, but not the obligation, to buy an agreed quantity of a particular commodity or financial instrument (the underlying) from the seller of the option at or before a certain time (the Expiration (options), expiration date) for a certain price (the strike price). This effectively gives the buyer a Long (finance), ''long'' position in the given asset. The seller (or "writer") is obliged to sell the commodity or financial instrument to the buyer if the buyer so decides. This effectively gives the seller a Short (finance), ''short'' position in the given asset. The buyer pays a fee (called a Insurance, premium) for this right. The term "call" comes from the fact that the owner has the right to "call the stock away" from the seller. Price of opt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
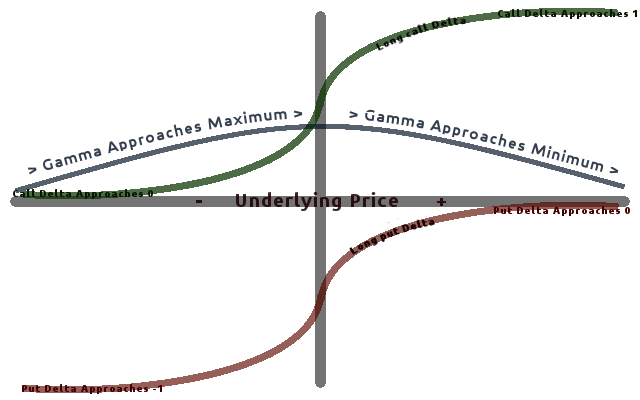
Delta (finance)
In mathematical finance, the Greeks are the quantities (known in calculus as partial derivatives; first-order or higher) representing the sensitivity of the price of a derivative instrument such as an option to changes in one or more underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters. Use of the Greeks The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging. The Greeks in the Black–Scholes model (a relatively simple idealised model o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance refers to monetary resources and to the study and Academic discipline, discipline of money, currency, assets and Liability (financial accounting), liabilities. As a subject of study, is a field of Business administration, Business Administration wich study the planning, organizing, leading, and controlling of an organization's resources to achieve its goals. Based on the scope of financial activities in financial systems, the discipline can be divided into Personal finance, personal, Corporate finance, corporate, and public finance. In these financial systems, assets are bought, sold, or traded as financial instruments, such as Currency, currencies, loans, Bond (finance), bonds, Share (finance), shares, stocks, Option (finance), options, Futures contract, futures, etc. Assets can also be banked, Investment, invested, and Insurance, insured to maximize value and minimize loss. In practice, Financial risk, risks are always present in any financial action and entities. Due ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Put Option
In finance, a put or put option is a derivative instrument in financial markets that gives the holder (i.e. the purchaser of the put option) the right to sell an asset (the ''underlying''), at a specified price (the ''strike''), by (or on) a specified date (the '' expiry'' or ''maturity'') to the ''writer'' (i.e. seller) of the put. The purchase of a put option is interpreted as a negative sentiment about the future value of the underlying stock. page 15 , 4.2.3 Positive and negative sentiment The term "put" comes from the fact that the owner has the right to "put up for sale" the stock or index. Puts may also be combined with other derivatives as part of more complex investment strategies, and in particular, may be useful for hedging. Holding a European put option is equivalent to holding the corresponding call option and selling an appropriate forward contract. This equivalence is called " put-call parity". Put options are most commonly used in the stock market to prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Option Time Value
In finance, the time value (TV) (''extrinsic'' or ''instrumental'' value) of an option (finance), option is the premium a rational investor would pay over its ''current'' exercise value (intrinsic value (finance), intrinsic value), based on the probability it will increase in value before expiry. For an Option style, American option this value is always greater than zero in a fair market, thus an option is ''always'' worth more than its current exercise value. As an option can be thought of as 'price insurance' (e.g., an airline insuring against unexpected soaring fuel costs caused by a hurricane), TV can be thought of as the ''risk premium'' the option seller charges the buyer—the higher the expected risk (volatility \cdot time), the higher the premium. Conversely, TV can be thought of as the price an investor is willing to pay for potential upside. Time value decays to zero at expiration, with a general rule that it will lose of its value during the first half of its life and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are not interchangeable; they are commonly distinguished by their position in an ordered tuple, or by a label, such as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the '' number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems, in the linear case, involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equations is devote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Option (finance)
In finance, an option is a contract which conveys to its owner, the ''holder'', the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset (or contingent liability) and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in '' over-the-counter'' (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts. Definition and application An option is a contract that allows the holder the right to buy or sell an underlying asset or financia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |