|
Metric (vector Bundle)
In differential geometry, the notion of a metric tensor can be extended to an arbitrary vector bundle, and to some principal fiber bundles. This metric is often called a bundle metric, or fibre metric. Definition If ''M'' is a topological manifold and : ''E'' → ''M'' a vector bundle on ''M'', then a metric on ''E'' is a bundle map ''k'' : ''E'' ×''M'' ''E'' → ''M'' × R from the fiber product of ''E'' with itself to the trivial bundle with fiber R such that the restriction of ''k'' to each fibre over ''M'' is a nondegenerate bilinear map of vector spaces.. Roughly speaking, ''k'' gives a kind of dot product (not necessarily symmetric or positive definite) on the vector space above each point of ''M'', and these products vary smoothly over ''M''. Properties Every vector bundle with paracompact base space can be equipped with a bundle metric. For a vector bundle of rank ''n'', this follows from the local trivialization, bundle charts \phi:\pi^(U)\to U\times\m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as classical antiquity, antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Nikolai Lobachevsky, Lobachevsky. The simplest examples of smooth spaces are the Differential geometry of curves, plane and space curves and Differential geometry of surfaces, surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Bundle
A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold M is a manifold TM which assembles all the tangent vectors in M . As a set, it is given by the disjoint unionThe disjoint union ensures that for any two points and of manifold the tangent spaces and have no common vector. This is graphically illustrated in the accompanying picture for tangent bundle of circle , see Examples section: all tangents to a circle lie in the plane of the circle. In order to make them disjoint it is necessary to align them in a plane perpendicular to the plane of the circle. of the tangent spaces of M . That is, : \begin TM &= \bigsqcup_ T_xM \\ &= \bigcup_ \left\ \times T_xM \\ &= \bigcup_ \left\ \\ &= \left\ \end where T_x M denotes the tangent space to M at the point x . So, an el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kaluza–Klein Theory
In physics, Kaluza–Klein theory (KK theory) is a classical unified field theory of gravitation and electromagnetism built around the idea of a fifth dimension beyond the common 4D of space and time and considered an important precursor to string theory. In their setup, the vacuum has the usual 3 dimensions of space and one dimension of time but with another microscopic extra spatial dimension in the shape of a tiny circle. Gunnar Nordström had an earlier, similar idea. But in that case, a fifth component was added to the electromagnetic vector potential, representing the Newtonian gravitational potential, and writing the Maxwell equations in five dimensions. The five-dimensional (5D) theory developed in three steps. The original hypothesis came from Theodor Kaluza, who sent his results to Albert Einstein in 1919 and published them in 1921. Kaluza presented a purely classical extension of general relativity to 5D, with a metric tensor of 15 components. Ten components are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
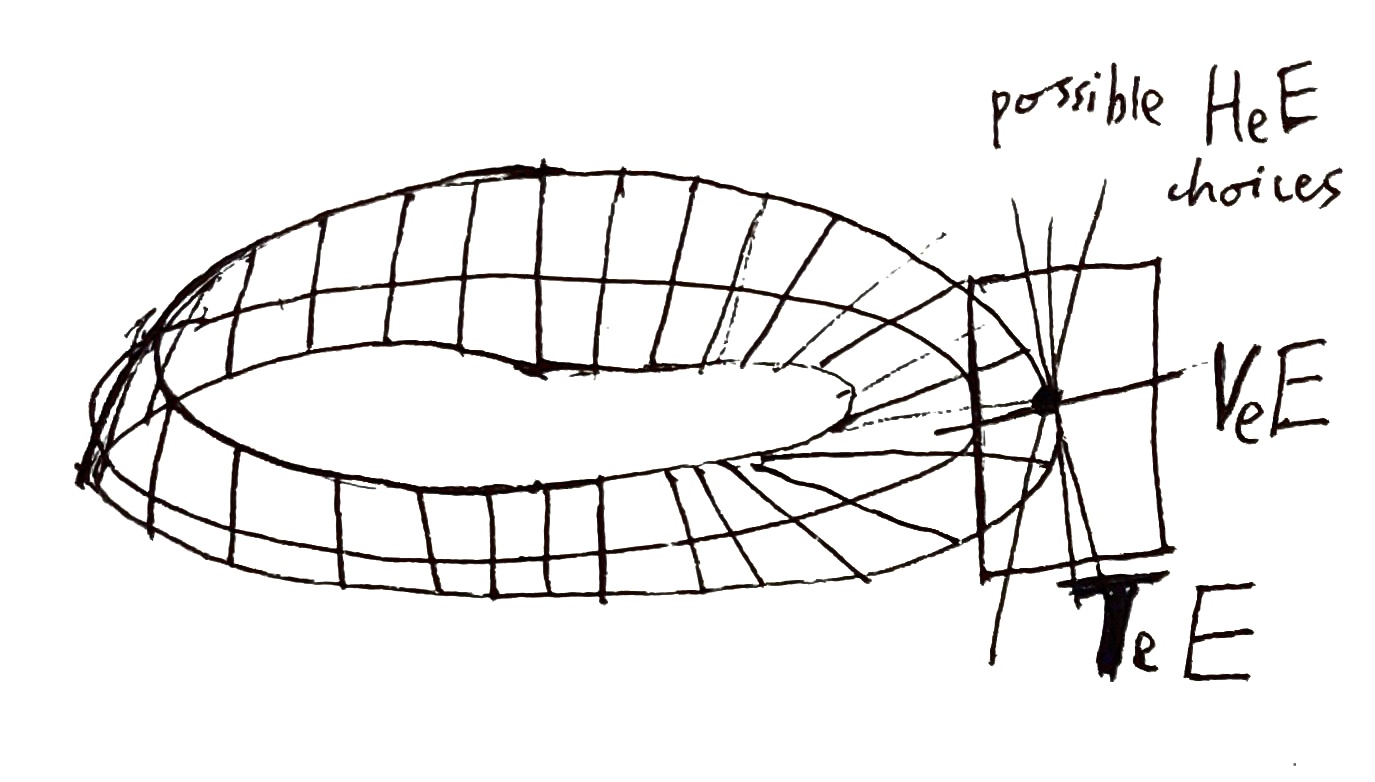
Vertical Subspace
In mathematics, the vertical bundle and the horizontal bundle are vector bundles associated to a smooth fiber bundle. More precisely, given a smooth fiber bundle \pi\colon E\to B, the vertical bundle VE and horizontal bundle HE are subbundles of the tangent bundle TE of E whose Whitney sum satisfies VE\oplus HE\cong TE. This means that, over each point e\in E, the fibers V_eE and H_eE form complementary subspaces of the tangent space T_eE. The vertical bundle consists of all vectors that are tangent to the fibers, while the horizontal bundle requires some choice of complementary subbundle. To make this precise, define the vertical space V_eE at e\in E to be \ker(d\pi_e). That is, the differential d\pi_e\colon T_eE\to T_bB (where b=\pi(e)) is a linear surjection whose kernel has the same dimension as the fibers of \pi. If we write F=\pi^(b), then V_eE consists of exactly the vectors in T_eE which are also tangent to F. The name is motivated by low-dimensional examples like the tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Space
In mathematics, the tangent space of a manifold is a generalization of to curves in two-dimensional space and to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold. Informal description In differential geometry, one can attach to every point x of a differentiable manifold a ''tangent space''—a real vector space that intuitively contains the possible directions in which one can tangentially pass through x . The elements of the tangent space at x are called the ''tangent vectors'' at x . This is a generalization of the notion of a vector, based at a given initial point, in a Euclidean space. The dimension of the tangent space at every point of a connected manifold is the same as that of the manifold itself. For example, if the given manifold is a 2 -sphere, then one can picture the tangent space at a point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connection Form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms. Historically, connection forms were introduced by Élie Cartan in the first half of the 20th century as part of, and one of the principal motivations for, his method of moving frames. The connection form generally depends on a choice of a coordinate frame, and so is not a tensorial object. Various generalizations and reinterpretations of the connection form were formulated subsequent to Cartan's initial work. In particular, on a principal bundle, a principal connection is a natural reinterpretation of the connection form as a tensorial object. On the other hand, the connection form has the advantage that it is a differential form defined on the differentiable manifold, rather than on an abstract principal bundle over it. Hence, despite their lack of tensoriality, connection forms continue to be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra Representation
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices (or endomorphisms of a vector space) in such a way that the Lie bracket is given by the commutator. In the language of physics, one looks for a vector space V together with a collection of operators on V satisfying some fixed set of commutation relations, such as the relations satisfied by the angular momentum operators. The notion is closely related to that of a representation of a Lie group. Roughly speaking, the representations of Lie algebras are the differentiated form of representations of Lie groups, while the representations of the universal cover of a Lie group are the integrated form of the representations of its Lie algebra. In the study of representations of a Lie algebra, a particular ring, called the universal enveloping algebra, associated with the Lie algebra plays an important role. The u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Associated Bundle
*
{{dab ...
Associated may refer to: *Associated, former name of Avon, Contra Costa County, California *Associated Hebrew Schools of Toronto, a school in Canada *Associated Newspapers, former name of DMG Media, a British publishing company See also *Association (other) *Associate (other) Associate may refer to: Academics * Associate degree, a two-year educational degree in the United States, and some areas of Canada * Associate professor, an academic rank at a college or university * Technical associate or Senmonshi, a Japa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Haar Measure
In mathematical analysis, the Haar measure assigns an "invariant volume" to subsets of locally compact topological groups, consequently defining an integral for functions on those groups. This Measure (mathematics), measure was introduced by Alfréd Haar in 1933, though its special case for Lie groups had been introduced by Adolf Hurwitz in 1897 under the name "invariant integral". Haar measures are used in many parts of mathematical analysis, analysis, number theory, group theory, representation theory, mathematical statistics, statistics, probability theory, and ergodic theory. Preliminaries Let (G, \cdot) be a locally compact space, locally compact Hausdorff space, Hausdorff topological group. The Sigma-algebra, \sigma-algebra generated by all open subsets of G is called the Borel algebra. An element of the Borel algebra is called a Borel set. If g is an element of G and S is a subset of G, then we define the left and right Coset, translates of S by ''g'' as follows: * Left ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pushforward (differential)
In differential geometry, pushforward is a linear approximation of smooth maps (formulating manifold) on tangent spaces. Suppose that \varphi\colon M\to N is a smooth map between smooth manifolds; then the differential of \varphi at a point x, denoted \mathrm d\varphi_x, is, in some sense, the best linear approximation of \varphi near x. It can be viewed as a generalization of the total derivative of ordinary calculus. Explicitly, the differential is a linear map from the tangent space of M at x to the tangent space of N at \varphi(x), \mathrm d\varphi_x\colon T_xM \to T_N. Hence it can be used to ''push'' tangent vectors on M ''forward'' to tangent vectors on N. The differential of a map \varphi is also called, by various authors, the derivative or total derivative of \varphi. Motivation Let \varphi: U \to V be a Smooth function#Smooth functions on and between manifolds, smooth map from an Open subset#Euclidean space, open subset U of \R^m to an open subset V of \R^n. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertical Bundle
In mathematics, the vertical bundle and the horizontal bundle are Vector bundle, vector bundles associated to a Fiber bundle#Differentiable fiber bundles, smooth fiber bundle. More precisely, given a smooth fiber bundle \pi\colon E\to B, the vertical bundle VE and horizontal bundle HE are Subbundle, subbundles of the tangent bundle TE of E whose Whitney sum satisfies VE\oplus HE\cong TE. This means that, over each point e\in E, the fibers V_eE and H_eE form complementary subspaces of the tangent space T_eE. The vertical bundle consists of all vectors that are tangent to the fibers, while the horizontal bundle requires some choice of complementary subbundle. To make this precise, define the vertical space V_eE at e\in E to be \ker(d\pi_e). That is, the differential d\pi_e\colon T_eE\to T_bB (where b=\pi(e)) is a linear surjection whose kernel has the same dimension as the fibers of \pi. If we write F=\pi^(b), then V_eE consists of exactly the vectors in T_eE which are also tangent t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |