|
Median Voting Rule
The median voting rule or median mechanism is a rule for group decision-making along a one-dimensional domain. Each person votes by writing down his/her ideal value, and the rule selects a single value which is (in the basic mechanism) the ''median'' of all votes. Motivation Many scenarions of group decision making involve a one-dimensional domain. Some examples are: * Members of a city-council have to decide on the total amount of annual city budget. * Several people working in the same office have to decide on the air-conditioning temperature. * Parents of schoolchildren should decide how long the annual school vacation should be. * The public has to decide where to locate a facility along a one-dimensional street. Each member has in mind an ideal decision, called his "peak". Each agent prefers the actual amount to be as close as possible to his peak. A simple way to decide is the ''average voting rule'': ask each member what is his peak, and take the average of all peak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
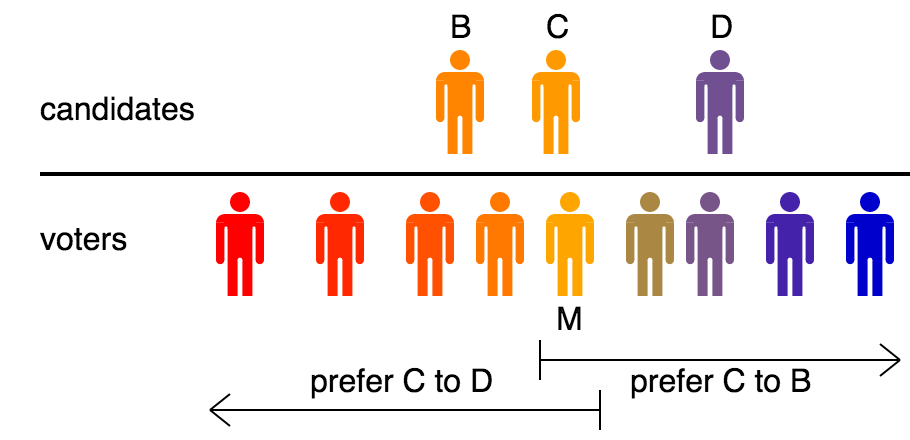
Median Voter Theorem
In political science and social choice theory, social choice, Black's median voter theorem says that if voters and candidates are distributed along a political spectrum, any voting method Condorcet criterion, compatible with majority-rule will elect the candidate preferred by the median voter. The median voter theorem thus shows that under a realistic model of voter behavior, Arrow's impossibility theorem, Arrow's theorem does not apply, and Decision theory, rational choice is possible for societies. The theorem was first derived by Duncan Black in 1948, and independently by Kenneth Arrow. Voting rules without this median voter property, like Instant-runoff voting, ranked choice voting, Plurality voting, plurality, and plurality-with-primaries have a Center-squeeze, center-squeeze effect that encourages candidates to take more extreme positions than the population would prefer. Similar median voter theorems exist for rules like score voting and approval voting when voters are either ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Preferences
In economics, convex preferences are an individual's ordering of various outcomes, typically with regard to the amounts of various goods consumed, with the property that, roughly speaking, "averages are better than the extremes". This implies that the consumer prefers a variety of goods to having more of a single good. The concept roughly corresponds to the concept of marginal utility#Diminishing marginal utility, diminishing marginal utility without requiring utility functions. Notation Comparable to the greater-than-or-equal-to Order theory#Partially ordered sets, ordering relation \geq for real numbers, the notation \succeq below can be translated as: 'is at least as good as' (in Preference (economics), preference satisfaction). Similarly, \succ can be translated as 'is strictly better than' (in preference satisfaction), and Similarly, \sim can be translated as 'is equivalent to' (in preference satisfaction). Definition Use ''x'', ''y'', and ''z'' to denote three consumpti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electoral Systems
An electoral or voting system is a set of rules used to determine the results of an election. Electoral systems are used in politics to elect governments, while non-political elections may take place in business, nonprofit organizations and informal organisations. These rules govern all aspects of the voting process: when elections occur, Suffrage, who is allowed to vote, Nomination rules, who can stand as a candidate, Voting method, how ballots are marked and cast, how the ballots are counted, how votes translate into the election outcome, limits on Campaign finance, campaign spending, and other factors that can affect the result. Political electoral systems are defined by constitutions and electoral laws, are typically conducted by election commissions, and can use multiple types of elections for different offices. Some electoral systems elect a single winner to a unique position, such as prime minister, president or governor, while others elect multiple winners, such as membe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dictatorship Mechanism
In social choice theory, a dictatorship mechanism is a degenerate voting rule or mechanism where the result depends on one person's. A serial dictatorship is similar, but also designates a series of "backup dictators", who break ties in the original dictator's choices when the dictator is indifferent. Formal definition Non-dictatorship is one of the necessary conditions in Arrow's impossibility theorem.''Game Theory'' Second Edition Guillermo Owen Ch 6 pp124-5 Axiom 5 Academic Press, 1982 In ''Social Choice and Individual Values'', Kenneth Arrow defines non-dictatorship as: :There is no voter i in such that, for every set of orderings in the domain of the constitution, and every pair of social states ''x'' and ''y'', ''x \succeq_i y'' implies x \succeq y. Unsurprisingly, a dictatorship is a rule that does not satisfy non-dictatorship. Anonymous voting rules automatically satisfy non-dictatorship (so long as there is more than one voter). Serial dictatorship When the dictator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbard–Satterthwaite Theorem
The Gibbard–Satterthwaite theorem is a theorem in social choice theory. It was first conjectured by the philosopher Michael Dummett and the mathematician Robin Farquharson in 1961 and then proved independently by the philosopher Allan Gibbard in 1973 and economist Mark Satterthwaite in 1975. It deals with deterministic ordinal electoral systems that choose a single winner, and shows that for every voting rule of this form, at least one of the following three things must hold: # The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or # The rule limits the possible outcomes to two alternatives only; or # The rule is not straightforward, i.e. there is no single always-best strategy (one that does not depend on other voters' preferences or behavior). Gibbard's proof of the theorem is more general and covers processes of collective decision that may not be ordinal, such as cardinal voting. Gibbard's 1978 theorem and Hylland's theorem are e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expressive Voting
Public choice, or public choice theory, is "the use of economic tools to deal with traditional problems of political science."Gordon Tullock, 9872008, "public choice," ''The New Palgrave Dictionary of Economics''. . It includes the study of political behavior. In political science, it is the subset of positive political theory that studies self-interested agents (voters, politicians, bureaucrats) and their interactions, which can be represented in a number of ways—using (for example) standard constrained utility maximization, game theory, or decision theory. It is the origin and intellectual foundation of contemporary work in political economics.Alberto Alesina, Torsten Persson, Guido Tabellini, 2006. “Reply to Blankart and Koester's Political Economics versus Public Choice Two Views of Political Economy in Competition,” Kyklos, 59(2), pp. 201–208 In popular use, "public choice" is often used as a shorthand for components of modern public choice theory that focus on how ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Highest Median Voting Rules
The highest median voting rules are a class of graded voting rules where the candidate with the highest median rating is elected. The various highest median rules differ in their treatment of ties, i.e., the method of ranking the candidates with the same median rating. Proponents of highest median rules argue that they provide the most faithful reflection of the voters' opinion. They note that as with other cardinal voting rules, highest medians are not subject to Arrow's impossibility theorem. However, critics note that highest median rules violate participation and the Archimedean property; highest median rules can fail to elect a candidate almost-unanimously preferred over all other candidates. Example As in score voting, voters rate candidates along a common scale, e.g.: An elector can give the same appreciation to several different candidates. A candidate not evaluated automatically receives the mention "Bad". Then, for each candidate, we calculate what percentage o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Method
A Condorcet method (; ) is an election method that elects the candidate who wins a majority of the vote in every head-to-head election against each of the other candidates, whenever there is such a candidate. A candidate with this property, the ''pairwise champion'' or ''beats-all winner'', is formally called the ''Condorcet winner'' or ''Pairwise Majority Rule Winner'' (PMRW). The head-to-head elections need not be done separately; a voter's choice within any given pair can be determined from the ranking. Some elections may not yield a Condorcet winner because voter preferences may be cyclic—that is, it is possible that every candidate has an opponent that defeats them in a two-candidate contest. The possibility of such cyclic preferences is known as the Condorcet paradox. However, a smallest group of candidates that beat all candidates not in the group, known as the Smith set, always exists. The Smith set is guaranteed to have the Condorcet winner in it should one exist. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
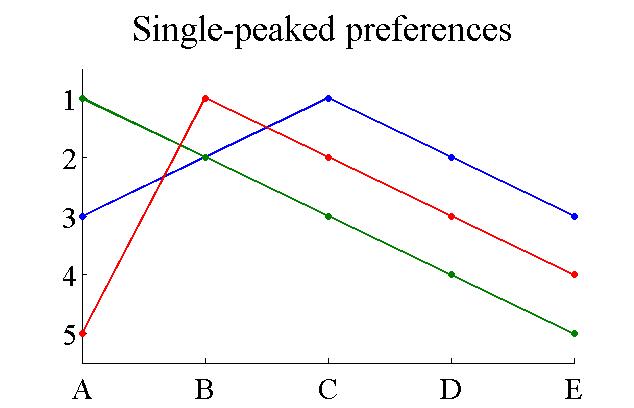
Single Peaked Preferences
Single-peaked preferences are a class of preference relations. A group has single-peaked preferences over a set of outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of Public good (economics), public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome, which is to select the median quantity; this results in the median voter theorem. It is truthful because the median function satisfies the Monotonicity (mechani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ranked Voting
Ranked voting is any voting system that uses voters' Ordinal utility, rankings of candidates to choose a single winner or multiple winners. More formally, a ranked vote system depends only on voters' total order, order of preference of the candidates. Ranked voting systems vary dramatically in how preferences are tabulated and counted, which gives them Comparison of voting rules, very different properties. In instant-runoff voting (IRV) and the single transferable vote system (STV), lower preferences are used as contingencies (back-up preferences) and are only applied when all higher-ranked preferences on a ballot have been eliminated or when the vote has been cast for a candidate who has been elected and surplus votes need to be transferred. Ranked votes of this type do not suffer the problem that a marked lower preference may be used against a voter's higher marked preference. Some ranked vote systems use ranks as weights; these systems are called positional voting. In the B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star-shaped Preferences
In social choice theory, star-shaped preferences are a class of preferences over points in a Euclidean space. An agent with star-shaped preferences has a unique ideal point (optimum), where he is maximally satisfied. Moreover, he becomes less and less satisfied as the actual distribution moves away from his optimum. Star-shaped preferences can be seen as a multi-dimensional extension of single-peaked preferences. Background Often, society has to choose a point from a subset of a Euclidean space. For example, society has to choose how to distribute its annual budget; each potential distribution is a vector of real numbers. If there are ''m'' potential issues in the budget, then the set of all potential budget distributions is a subset of R''m'' - the m-dimensional Euclidean space. Different members of society may have different preferences over budget distributions. A ''preference'' is any total order over points. For example, a particular agent may state that he prefers the distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |