|
Math Walk
A math walk, or math trail, is a type of themed walk in the US, where direct experience is translated into the language of mathematics or abstract mathematical sciences such as information science, computer science, decision science, or probability and statistics. Some sources specify how to create a math walk whereas others define a math walk at a specific location such as a junior high school or in Boston. The journal The Mathematics Teacher includes a special section titled ''"Mathematical Lens"'' in many issues with the metaphor of lens capturing seeing the world as mathematics. Informal learning The idea that ''"math is everywhere"'', which is emphasized on a math walk, is captured by the philosophy of mathematicism with its early adherents, Pythagoras and Plato. The math walk also implicitly involves experiencing math via modeling since mathematics serves to model what we sense. The math walk is a form of informal learning, often in an outside environment or in a museum. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Themed Walk
A themed walk is a type of informal learning and often is defined by a walk along which there are information boards or other identifying codes (e.g. QR codes) covering a specific topic or theme such as history, geology or forestry. An academic discipline or school subject can define a theme. A walk can consist of one or more themes. Whilst themed walks are often designed to encourage walking, educational paths and nature trail tend to be aimed more at educating or training. Themes For nature-based themes, paths may be several kilometres long and may be used both for educational purposes and recreation. They may connect places, buildings or natural features that have a particular theme in common by a signed route, but may also have specifically positioned exhibits. For science themes, informal learning provides ways to engage in diverse settings. For themes related to the nature, features of nature (e.g. raised bogs or biotopes) or of geology may be laid out as special ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semantic Network
A semantic network, or frame network is a knowledge base that represents semantic relations between concepts in a network. This is often used as a form of knowledge representation. It is a directed or undirected graph consisting of vertices, which represent concepts, and edges, which represent semantic relations between concepts, mapping or connecting semantic fields. A semantic network may be instantiated as, for example, a graph database or a concept map. Typical standardized semantic networks are expressed as semantic triples. Semantic networks are used in natural language processing applications such as semantic parsing and word-sense disambiguation. Semantic networks can also be used as a method to analyze large texts and identify the main themes and topics (e.g., of social media posts), to reveal biases (e.g., in news coverage), or even to map an entire research field. History Examples of the use of semantic networks in logic, directed acyclic graphs as a mnemonic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
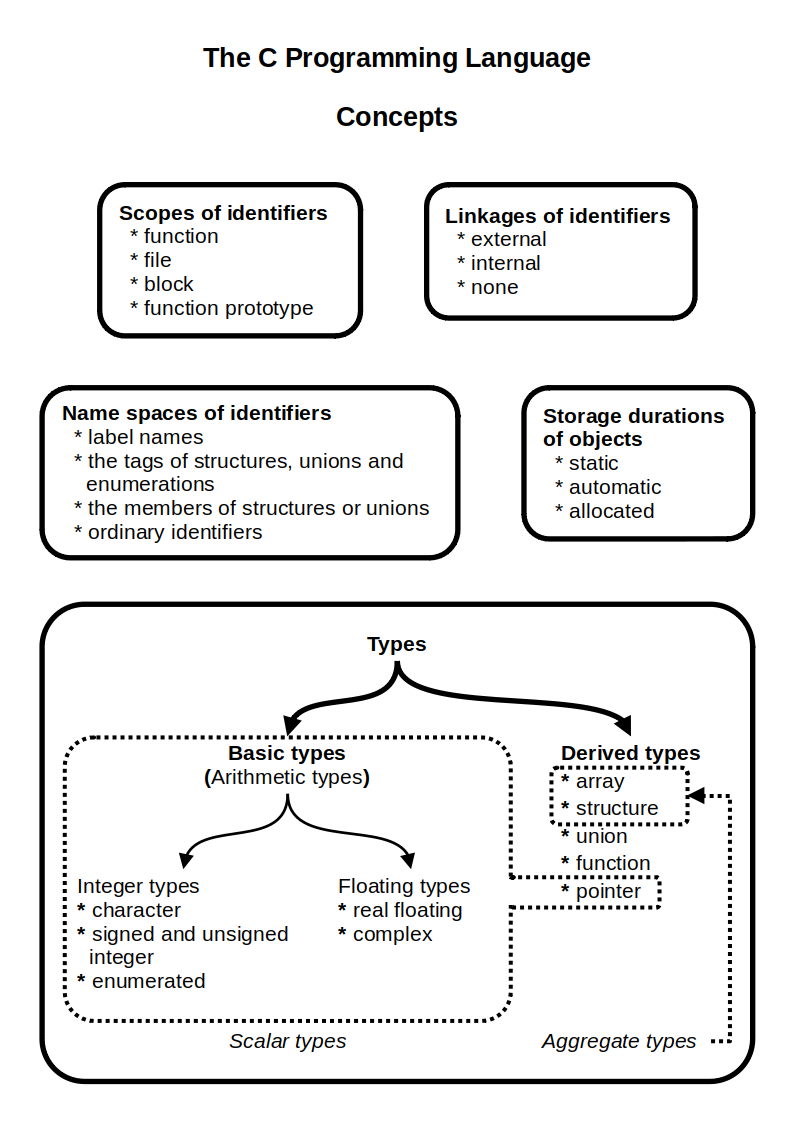
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python (programming Language)
Python is a high-level programming language, high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is type system#DYNAMIC, dynamically type-checked and garbage collection (computer science), garbage-collected. It supports multiple programming paradigms, including structured programming, structured (particularly procedural programming, procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC (programming language), ABC programming language, and he first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000. Python 3.0, released in 2008, was a major revision not completely backward-compatible with earlier versions. Python 2.7.18, released in 2020, was the last release of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, Graph (discrete mathematics), graphs, and Statement (logic), statements in Mathematical logic, logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumeration, enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Programming
Computer programming or coding is the composition of sequences of instructions, called computer program, programs, that computers can follow to perform tasks. It involves designing and implementing algorithms, step-by-step specifications of procedures, by writing source code, code in one or more programming languages. Programmers typically use high-level programming languages that are more easily intelligible to humans than machine code, which is directly executed by the central processing unit. Proficient programming usually requires expertise in several different subjects, including knowledge of the Domain (software engineering), application domain, details of programming languages and generic code library (computing), libraries, specialized algorithms, and Logic#Formal logic, formal logic. Auxiliary tasks accompanying and related to programming include Requirements analysis, analyzing requirements, Software testing, testing, debugging (investigating and fixing problems), imple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iteration
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. In mathematics and computer science, iteration (along with the related technique of recursion) is a standard element of algorithms. Mathematics In mathematics, iteration may refer to the process of iterated function, iterating a function, i.e. applying a function repeatedly, using the output from one iteration as the input to the next. Iteration of apparently simple functions can produce complex behaviors and difficult problems – for examples, see the Collatz conjecture and juggler sequences. Another use of iteration in mathematics is in iterative methods which are used to produce approximate numerical solutions to certain mathematical problems. Newton's method is an example of an iterative method. Manual calculation of a number's sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Railroad Tie
A railroad tie, crosstie (American English), railway tie (Canadian English) or railway sleeper ( Australian and British English) is a rectangular support for the rails in railroad tracks. Generally laid perpendicular to the rails, ties transfer loads to the track ballast and subgrade, hold the rails upright and keep them spaced to the correct gauge. Railroad ties are traditionally made of wood, but prestressed concrete is now also widely used, especially in Europe and Asia. Steel ties are common on secondary lines in the UK; plastic composite ties are also employed, although far less than wood or concrete. As of January 2008, the approximate market share in North America for traditional and wood ties was 91.5%, the remainder being concrete, steel, azobé (red ironwood) and plastic composite. Tie spacing may depend on the type of tie, traffic loads and other requirements, for example on North American mainline railroads to on London, Midland and Scottish Railway joi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Sense
In psychology, number sense is the term used for the hypothesis that some animals, particularly humans, have a biologically determined ability that allows them to represent and manipulate large numerical quantities. The term was popularized by Stanislas Dehaene in his 1997 book "The Number Sense," but originally named by the mathematician Tobias Dantzig in his 1930 text Number: The Language of Science. Psychologists believe that the number sense in humans can be differentiated into the approximate number system, a system that supports the estimation of the magnitude, and the parallel individuation system, which allows the tracking of individual objects, typically for quantities below 4. There are also some differences in how number sense is defined in math cognition. For example, Gersten and Chard say number sense "refers to a child's fluidity and flexibility with numbers, the sense of what numbers mean and an ability to perform mental mathematics and to look at the world ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |