|
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan "Bertus" Brouwer (27 February 1881 – 2 December 1966) was a Dutch mathematician and philosopher who worked in topology, set theory, measure theory and complex analysis. Regarded as one of the greatest mathematicians of the 20th century, he is known as one of the founders of modern topology, particularly for establishing his fixed-point theorem and the topological invariance of dimension. Brouwer also became a major figure in the philosophy of intuitionism, a constructivist school of mathematics which argues that math is a cognitive construct rather than a type of objective truth. This position led to the Brouwer–Hilbert controversy, in which Brouwer sparred with his formalist colleague David Hilbert. Brouwer's ideas were subsequently taken up by his student Arend Heyting and Hilbert's former student Hermann Weyl. In addition to his mathematical work, Brouwer also published the short philosophical tract ''Life, Art, and Mysticism'' (1905). Biography B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overschie
Overschie () is a neighborhood of Rotterdam, Netherlands, formerly a separate village with its own municipality. The village of Overschie was located on the intersection of four rivers called "Schie": the Delftsche Schie, Schiedamsche Schie, Delfshavensche Schie, and Rotterdamsche Schie. It was a separate municipality between 1817 and 1941, when it merged with Rotterdam. Immediately after the Second World War, the construction of a large suburb was begun southeast of the village. "Overschie" is now also the name of a ''deelgemeente'' (borough) of the city of Rotterdam, covering the former village, the neighborhood Overschie, Zestienhoven (which also holds the Rotterdam The Hague Airport), and the countryside to the north including the hamlet Zweth. image:Overschie 1867.png, 180px, none, Overschie in 1867. References [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indecomposability (constructive Mathematics)
In intuitionistic analysis and in computable analysis, indecomposability or indivisibility (, from the adjective ''unzerlegbar'') is the principle that the continuum cannot be partitioned into two nonempty pieces. This principle was established by Brouwer in 1928 English translation of §1 see p.490–492 of: using intuitionistic principles, and can also be proven using Church's thesis. The analogous property in classical analysis is the fact that every continuous function from the continuum to is constant. It follows from the indecomposability principle that any property of real numbers that is ''decided'' (each real number either has or does not have that property) is in fact trivial (either all the real numbers have that property, or else none of them do). Conversely, if a property of real numbers is not trivial, then the property is not decided for all real numbers. This contradicts the law of the excluded middle, according to which every property of the real nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Theory
Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathematics – is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of ''naive set theory''. After the discovery of Paradoxes of set theory, paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Torsion (mechanics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a Set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of List of continuity-related mathematical topics, continuity. Euclidean spaces, and, more generally, metric spaces are examples of topological spaces, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and Homotopy, homotopies. A property that is invariant under such deformations is a to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosopher
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational and critical inquiry that reflects on its methods and assumptions. Historically, many of the individual sciences, such as physics and psychology, formed part of philosophy. However, they are considered separate academic disciplines in the modern sense of the term. Influential traditions in the history of philosophy include Western philosophy, Western, Islamic philosophy, Arabic–Persian, Indian philosophy, Indian, and Chinese philosophy. Western philosophy originated in Ancient Greece and covers a wide area of philosophical subfields. A central topic in Arabic–Persian philosophy is the relation between reason and revelation. Indian philosophy combines the Spirituality, spiritual problem of how to reach Enlightenment in Buddhism, enlighten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians was Thales of Miletus (); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem. The number of known mathematicians grew when Pythagoras of Samos () established the Pythagorean school, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bohr Brouwer Zurich1932
Niels Henrik David Bohr (, ; ; 7 October 1885 – 18 November 1962) was a Danish theoretical physicist who made foundational contributions to understanding atomic structure and quantum theory, for which he received the Nobel Prize in Physics in 1922. Bohr was also a philosopher and a promoter of scientific research. Bohr developed the Bohr model of the atom, in which he proposed that energy levels of electrons are discrete and that the electrons revolve in stable orbits around the atomic nucleus but can jump from one energy level (or orbit) to another. Although the Bohr model has been supplanted by other models, its underlying principles remain valid. He conceived the principle of complementarity: that items could be separately analysed in terms of contradictory properties, like behaving as a wave or a stream of particles. The notion of complementarity dominated Bohr's thinking in both science and philosophy. Bohr founded the Institute of Theoretical Physics at the Unive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hendrik Albertus Brouwer
Hendrik Albertus Brouwer (20 September 1886 – 18 September 1973) was a Dutch geologist who specialized in petrology and explored South Africa and the Dutch colonies in Indonesia. Brouwer was born in Medemblik, the son of Egbertus L. Brouwer and Hendrika Poutsma. After schooling in Haarlem he went to the Technical University in Delft to study mine engineering and obtained a diploma in 1908. He received a doctoral degree for a dissertation on South African nepheline syenites in 1910. He became a professor of geology at the Delft Technical University in 1918 and during his career he travelled to Brazil, North America, South Africa and parts of southeast Asia to conduct studies on rocks. He also edited the first volume of a series on ''Practical Hints to Scientific Travellers'' in 1925. He became a professor at the University of Amsterdam in 1928, succeeding Eugène Dubois and worked there until his retirement in 1956. An extinct genus of tarpon relative, '' Brouweria'', is name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biographical Memoirs Of Fellows Of The Royal Society
The ''Biographical Memoirs of Fellows of the Royal Society'' is an academic journal on the history of science published annually by the Royal Society. It publishes obituaries of Fellows of the Royal Society. It was established in 1932 as ''Obituary Notices of Fellows of the Royal Society'' and obtained its current title in 1955, with volume numbering restarting at 1. Prior to 1932, obituaries were published in the '' Proceedings of the Royal Society''. The memoirs are a significant historical record and most include a full bibliography of works by the subjects. The memoirs are often written by a scientist of the next generation, often one of the subject's own former students, or a close colleague. In many cases the author is also a Fellow. Notable biographies published in this journal include Albert Einstein, Alan Turing, Bertrand Russell Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British philosopher, logician, mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Society
The Royal Society, formally The Royal Society of London for Improving Natural Knowledge, is a learned society and the United Kingdom's national academy of sciences. The society fulfils a number of roles: promoting science and its benefits, recognising excellence in science, supporting outstanding science, providing scientific advice for policy, education and public engagement and fostering international and global co-operation. Founded on 28 November 1660, it was granted a royal charter by Charles II of England, King Charles II and is the oldest continuously existing scientific academy in the world. The society is governed by its Council, which is chaired by the society's president, according to a set of statutes and standing orders. The members of Council and the president are elected from and by its Fellows, the basic members of the society, who are themselves elected by existing Fellows. , there are about 1,700 fellows, allowed to use the postnominal title FRS (Fellow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism (opposed to preintuitionism), is an approach where mathematics is considered to be purely the result of the constructive mental activity of humans rather than the discovery of fundamental principles claimed to exist in an objective reality. That is, logic and mathematics are not considered analytic activities wherein deep properties of objective reality are revealed and applied, but are instead considered the application of internally consistent methods used to realize more complex mental constructs, regardless of their possible independent existence in an objective reality. Truth and proof The fundamental distinguishing characteristic of intuitionism is its interpretation of what it means for a mathematical statement to be true. In Luitzen Egbertus Jan Brouwer, Brouwer's original intuitionism, the truth of a mathematical statement is a subjective claim: a mathematical statement corresponds to a mental construc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
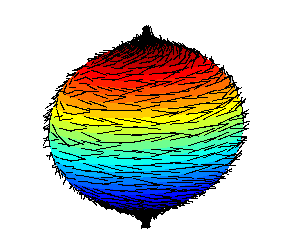
Hairy Ball Theorem
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous function, continuous tangent vector field on even-dimensional n‑sphere, ''n''-spheres. For the ordinary sphere, or 2‑sphere, if ''f'' is a continuous function that assigns a Vector (geometric), vector in to every point ''p'' on a sphere such that ''f''(''p'') is always tangent to the sphere at ''p'', then there is at least one pole, a point where the field vanishes (a ''p'' such that ''f''(''p'') = Null vector, 0). The theorem was first proved by Henri Poincaré for the 2-sphere in 1885, and extended to higher even dimensions in 1912 by Luitzen Egbertus Jan Brouwer. The theorem has been expressed colloquially as "you can't comb a hairy ball flat without creating a cowlick" or "you can't comb the hair on a coconut". Counting zeros Every zero of a vector field has a (non-zero) "Vector field#Index of a vector field, index", and it ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |