|
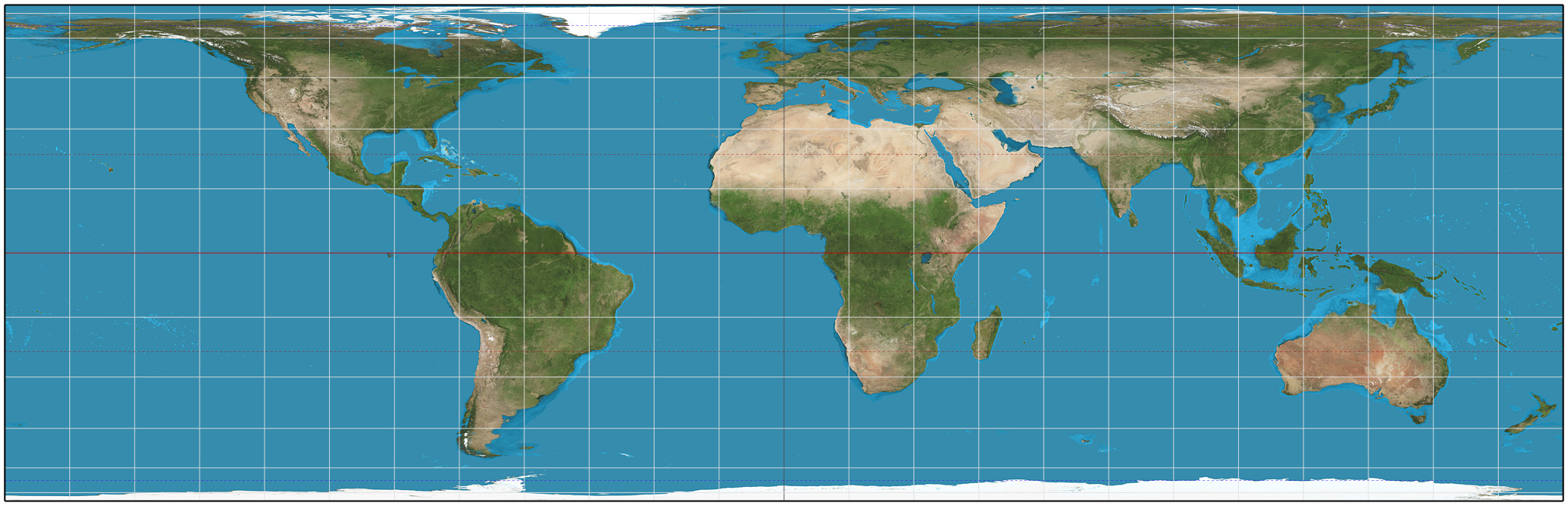
Loximuthal Projection
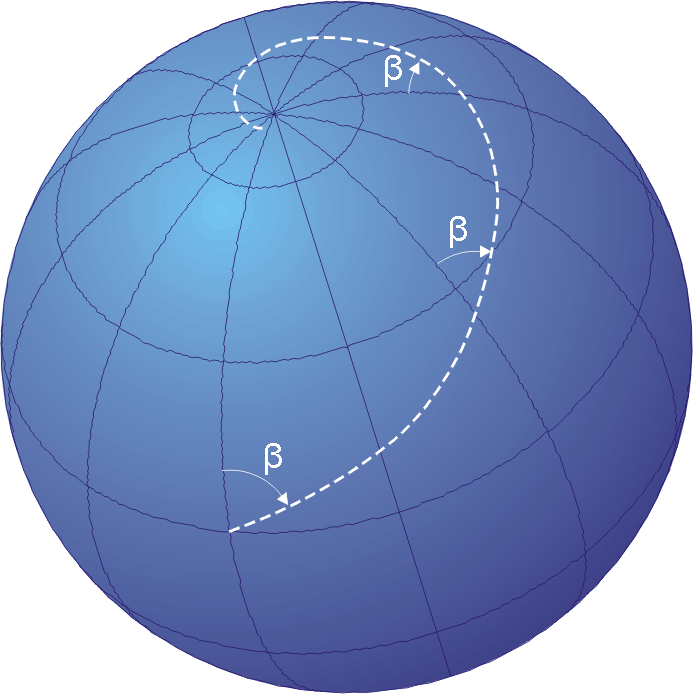
In cartography, the loximuthal projection is a map projection introduced by Karl Siemon in 1935, and independently in 1966 by Waldo R. Tobler, who named it. It is characterized by the fact that loxodromes (rhumb lines) from one chosen central point (the intersection of the central meridian and central latitude) are shown straight lines, correct in azimuth from the center, and are "true to scale" in the sense that distances measured along such lines are proportional to lengths of the corresponding rhumb lines on the surface of the Earth. It is neither an equal-area projection nor conformal. Description A loxodrome on the surface of the Earth is a curve of constant bearing: it meets every parallel of latitude at the same angle. Suppose its bearing is ''θ'' north of east, so, for example, due east is ''θ'' = 0; due north is ''θ'' = a right angle; due west is ''θ'' = a half circle. The loxodrome's whole length as it goes fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartography
Cartography (; from grc, χάρτης , "papyrus, sheet of paper, map"; and , "write") is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can be modeled in ways that communicate spatial information effectively. The fundamental objectives of traditional cartography are to: * Set the map's agenda and select traits of the object to be mapped. This is the concern of map editing. Traits may be physical, such as roads or land masses, or may be abstract, such as toponyms or political boundaries. * Represent the terrain of the mapped object on flat media. This is the concern of map projections. * Eliminate characteristics of the mapped object that are not relevant to the map's purpose. This is the concern of generalization. * Reduce the complexity of the characteristics that will be mapped. This is also the concern of generalization. * Orchestrate the elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characterization (mathematics)
In mathematics, a characterization of an object is a set of conditions that, while different from the definition of the object, is logically equivalent to it. To say that "Property ''P'' characterizes object ''X''" is to say that not only does ''X'' have property ''P'', but that ''X'' is the ''only'' thing that has property ''P'' (i.e., ''P'' is a defining property of ''X''). Similarly, a set of properties ''P'' is said to characterize ''X'', when these properties distinguish ''X'' from all other objects. Even though a characterization identifies an object in a unique way, several characterizations can exist for a single object. Common mathematical expressions for a characterization of ''X'' in terms of ''P'' include "''P'' is necessary and sufficient for ''X''", and "''X'' holds if and only if ''P''". It is also common to find statements such as "Property ''Q'' characterizes ''Y'' up to isomorphism". The first type of statement says in different words that the extension of ''P' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loxodrome
In navigation, a rhumb line, rhumb (), or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north. Introduction The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese mathematician Pedro Nunes in 1537, in his ''Treatise in Defense of the Marine Chart'', with further mathematical development by Thomas Harriot in the 1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature, whereas a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian (geography)
In geography and geodesy, a meridian is the locus connecting points of equal longitude, which is the angle (in degrees or other units) east or west of a given prime meridian (currently, the IERS Reference Meridian). In other words, it is a line of longitude. The position of a point along the meridian is given by that longitude and its latitude, measured in angular degrees north or south of the Equator. On a Mercator projection or on a Gall-Peters projection, each meridian is perpendicular to all circles of latitude. A meridian is half of a great circle on Earth's surface. The length of a meridian on a modern ellipsoid model of Earth ( WGS 84) has been estimated as . Pre-Greenwich The first prime meridian was set by Eratosthenes in 200 BCE. This prime meridian was used to provide measurement of the earth, but had many problems because of the lack of latitude measurement. Many years later around the 19th century there were still concerns of the prime meridian. Multiple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or '' normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the oce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuth
An azimuth (; from ar, اَلسُّمُوت, as-sumūt, the directions) is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north. Mathematically, the relative position vector from an observer ( origin) to a point of interest is projected perpendicularly onto a reference plane (the horizontal plane); the angle between the projected vector and a reference vector on the reference plane is called the azimuth. When used as a celestial coordinate, the azimuth is the horizontal direction of a star or other astronomical object in the sky. The star is the point of interest, the reference plane is the local area (e.g. a circular area with a 5 km radius at sea level) around an observer on planetary surface, Earth's surface, and the reference vector points to true north. The azimuth is the angle between the north vector and the star's vector on the horizontal plane In astronomy, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal-area Projection
In cartography, an equal-area projection is a map projection that preserves area measure, generally distorting shapes in order to do that. Equal-area maps are also called equivalent or authalic. An equal-area map projection cannot be conformal, nor can a conformal map projection be equal-area. Several equivalent projections were developed in an attempt to minimize the distortion of countries and continents of planet Earth, keeping the area constant. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, etc. Description Equal area representation implies that a region of interest in a particular portion of the map will share the same proportion of area as in any other part of the map. Statistical grid The term "statistical grid" refers to a discrete grid (global or local) of an equal-area surface representation, used for data visualization, geocode and statistical spatial analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Of Latitude
A circle of latitude or line of latitude on Earth is an abstract east–west small circle connecting all locations around Earth (ignoring elevation) at a given latitude coordinate line. Circles of latitude are often called parallels because they are parallel to each other; that is, planes that contain any of these circles never intersect each other. A location's position along a circle of latitude is given by its longitude. Circles of latitude are unlike circles of longitude, which are all great circles with the centre of Earth in the middle, as the circles of latitude get smaller as the distance from the Equator increases. Their length can be calculated by a common sine or cosine function. The 60th parallel north or south is half as long as the Equator (disregarding Earth's minor flattening by 0.335%). On the Mercator projection or on the Gall-Peters projection, a circle of latitude is perpendicular to all meridians. On the ellipsoid or on spherical projection, all circles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable Notability is the property of being worthy of notice, having fame, or being considered to be of a high degree of interest, significance, or distinction. It also refers to the capacity to be such. Persons who are notable due to public responsibi .... Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection ; Cylindrical: In standard presentation, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In standard presentation, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In standard presentation, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |