|
Logarithmic Sobolev Inequalities
In mathematics, logarithmic Sobolev inequalities are a class of inequalities involving the norm of a function ''f'', its logarithm, and its gradient \nabla f . These inequalities were discovered and named by Leonard Gross, who established them in dimension-independent form, in the context of constructive quantum field theory. Similar results were discovered by other mathematicians before and many variations on such inequalities are known. Gross proved the inequality: \int_\big, f(x)\big, ^2 \log\big, f(x)\big, \,d\nu(x) \leq \int_\big, \nabla f(x)\big, ^2 \,d\nu(x) +\, f\, _2^2\log \, f\, _2, where \, f\, _2 is the L^2(\nu)-norm of f, with \nu being standard Gaussian measure on \mathbb^n. Unlike classical Sobolev inequalities, Gross's log-Sobolev inequality does not have any dimension-dependent constant, which makes it applicable in the infinite-dimensional limit. Entropy functional Define the entropy functional\operatorname_\mu(f) = \int (f \ln f) d\mu - \int f \ln ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonard Gross
Leonard Gross (born February 24, 1931) is an American mathematician and Professor Emeritus of Mathematics at Cornell University. Gross has made fundamental contributions to mathematics and the mathematically rigorous study of quantum field theory. Education and career Leonard Gross graduated from James Madison High School in December 1948. He was awarded an Emil Schweinberg scholarship that enabled him to attend college. He studied at City College of New York for one term and then studied electrical engineering at Cooper Union for two years. He then transferred to the University of Chicago, where he obtained a master's degree in physics and mathematics (1954) and a Ph.D. in mathematics (1958). Gross taught at Yale University and was awarded a National Science Foundation Fellowship in 1959. He joined the faculty of the mathematics department of Cornell University in 1960. Gross was a member of the Institute for Advanced Study in 1959 and in 1983 and has held other visiting posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructive Quantum Field Theory
In mathematical physics, constructive quantum field theory is the field devoted to showing that quantum field theory can be defined in terms of precise mathematical structures. This demonstration requires new mathematics, in a sense analogous to classical real analysis, putting calculus on a mathematically rigorous foundation. Weak, strong, and electromagnetic forces of nature are believed to have their natural description in terms of quantum fields. Attempts to put quantum field theory on a basis of completely defined concepts have involved most branches of mathematics, including functional analysis, differential equations, probability theory, representation theory, geometry, and topology. It is known that a ''quantum field'' is inherently hard to handle using conventional mathematical techniques like explicit estimates. This is because a quantum field has the general nature of an operator-valued distribution, a type of object from mathematical analysis. The existence the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space \mathbb^n, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces. Gaussian measures are named after the German mathematician Carl Friedrich Gauss. One reason why Gaussian measures are so ubiquitous in probability theory is the central limit theorem. Loosely speaking, it states that if a random variable X is obtained by summing a large number N of independent random variables with variance 1, then X has variance N and its law is approximately Gaussian. Definitions Let n \in N and let B_0(\mathbb^n) denote the completion of the Borel \sigma-algebra on \mathbb^n. Let \lambda^n : B_0(\mathbb^n) \to , +\infty/math> denote the usual n-dimensional Lebesgue measure. Then the standard Gaussian measure \gamma^n : B_0(\mathbb^n) \to , 1/math> is defined by \gamma^ (A) = \frac \int_ \exp \left( - \frac \left\, x \right\, _^ \right) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sobolev Inequalities
In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under slightly stronger conditions some Sobolev spaces are compactly embedded in others. They are named after Sergei Lvovich Sobolev. Sobolev embedding theorem Let denote the Sobolev space consisting of all real-valued functions on whose weak derivatives up to order are functions in . Here is a non-negative integer and . The first part of the Sobolev embedding theorem states that if , and are two real numbers such that :\frac-\frac = \frac -\frac, (given n, p, k and \ell this is satisfied for some q \in [1, \infty) provided (k- \ell) p n, the embedding criterion will hold with r=0 and some positive value of \alpha. That is, for a function f on \mathbb R^n, if f has k derivatives in L^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
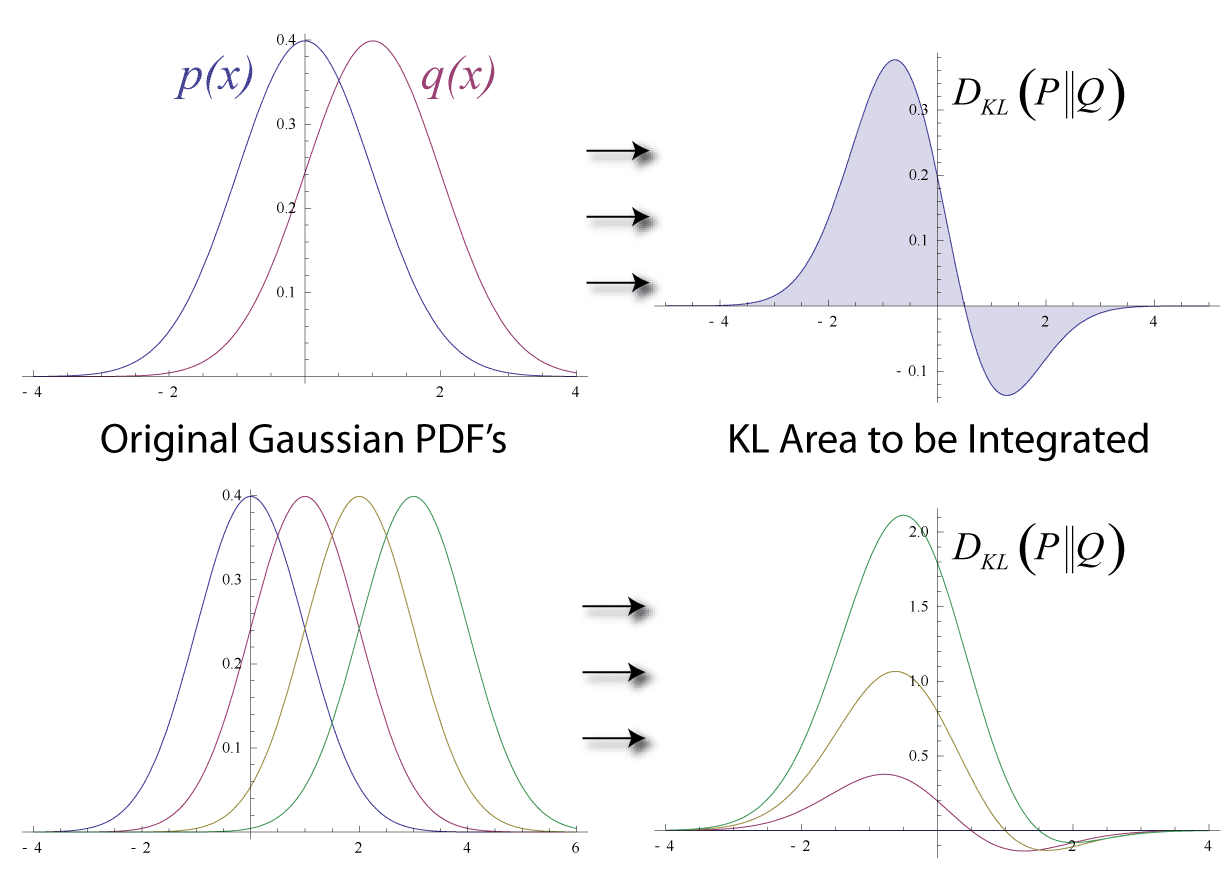
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiomatic Quantum Field Theory
Axiomatic quantum field theory is a mathematical discipline which aims to describe quantum field theory in terms of rigorous axioms. It is strongly associated with functional analysis and operator algebras, but has also been studied in recent years from a more geometric and functorial perspective. There are two main challenges in this discipline. First, one must propose a set of axioms which describe the general properties of any mathematical object that deserves to be called a "quantum field theory". Then, one gives rigorous mathematical constructions of examples satisfying these axioms. Analytic approaches Wightman axioms The first set of axioms for quantum field theories, known as the Wightman axioms, were proposed by Arthur Wightman in the early 1950s. These axioms attempt to describe QFTs on flat Minkowski spacetime by regarding quantum fields as operator-valued distributions acting on a Hilbert space. In practice, one often uses the Wightman reconstruction theorem, whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sobolev Spaces
In mathematics, a Sobolev space is a vector space of functions equipped with a normed space, norm that is a combination of Lp norm, ''Lp''-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak derivative, weak sense to make the space Complete metric space, complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function. Sobolev spaces are named after the Russian mathematician Sergei Lvovich Sobolev, Sergei Sobolev. Their importance comes from the fact that Weak solution, weak solutions of some important partial differential equations exist in appropriate Sobolev spaces, even when there are no strong solutions in spaces of continuous functions with the derivatives understood in the classical sense. Motivat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |