|
Line-cylinder Intersection
Line-cylinder intersection is the calculation of any points of Intersection (geometry), intersection, given an analytic geometry description of a Line (geometry), line and a Cylinder (geometry), cylinder in 3d space. An arbitrary line and cylinder may have no intersection at all. Or there may be one or two points of intersection. Or a line may lie along the surface of a cylinder, parallel to its axis, resulting in infinitely many points of intersection. The method described here distinguishes between these cases, and when intersections exist, computes their positions. The term “cylinder” can refer to a Solid geometry, three-dimensional solid or, as in this article, only the curved external Surface#In mathematics, surface of the solid. This is why a line piercing a cylinder's volume is considered to have two points of intersection: the surface point where it enters and the one where it leaves. See #End caps, § end caps. A key intuition of this sort of intersection problem is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Simulation
A simulation is an imitative representation of a process or system that could exist in the real world. In this broad sense, simulation can often be used interchangeably with model. Sometimes a clear distinction between the two terms is made, in which simulations require the use of models; the model represents the key characteristics or behaviors of the selected system or process, whereas the simulation represents the evolution of the model over time. Another way to distinguish between the terms is to define simulation as experimentation with the help of a model. This definition includes time-independent simulations. Often, computers are used to execute the simulation. Simulation is used in many contexts, such as simulation of technology for performance tuning or optimizing, safety engineering, testing, training, education, and video games. Simulation is also used with scientific modelling of natural systems or human systems to gain insight into their functioning, as in economic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry. Analytic geometry is used in physics and engineering, and also in aviation, Aerospace engineering, rocketry, space science, and spaceflight. It is the foundation of most modern fields of geometry, including Algebraic geometry, algebraic, Differential geometry, differential, Discrete geometry, discrete and computational geometry. Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and circles, often in two and sometimes three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space. As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometric shapes in a numerical way and extracting numerical information from shapes' numerical definitions and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eric Haines
Eric Haines is an American software engineer and expert in computer graphics, specifically image rendering. he is with NVIDIA Corporation as Distinguished Engineer. He is a co-author of the book ''Real-Time Rendering'', currently in its fourth edition.Tomas Akenine-Möller, Eric Haines, Naty Hoffman, Angelo Pesce, Michał Iwanicki, and Sébastien Hillaire''Real-Time Rendering'' A K Peters/CRC Press, 4th edition: 2018, 1198pp. * 3rd edition: Tomas Akenine-Möller, Eric Haines, and Naty Hoffman, ''Real-Time Rendering'', Natick: A.K. Peters Ltd., 3rd edition: 2008, 1045pp. * 2nd edition: Tomas Akenine-Möller, Eric Haines, ''Real-Time Rendering'', Natick: A.K. Peters Ltd., 2002, 900pp. * 1st edition: Tomas Möller, Eric Haines, ''Real-Time Rendering'', 1999, 512pp. Eric Haines earned an M.S. in 1986 from Cornell University. His thesis was ''The Light Buffer: A Ray Tracer Shadow Testing Accelerator''. An image created by software based on the thesis was used on the September ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line–plane Intersection
In analytic geometry, the intersection of a line and a plane in three-dimensional space can be the empty set, a point, or a line. It is the entire line if that line is embedded in the plane, and is the empty set if the line is parallel to the plane but outside it. Otherwise, the line cuts through the plane at a single point. Distinguishing these cases, and determining equations for the point and line in the latter cases, have use in computer graphics, motion planning, and collision detection. Algebraic form In vector notation, a plane can be expressed as the set of points \mathbf for which :(\mathbf-\mathbf)\cdot\mathbf = 0 where \mathbf is a normal vector to the plane and \mathbf is a point on the plane. (The notation \mathbf\cdot\mathbf denotes the dot product of the vectors \mathbf and \mathbf.) The vector equation for a line is :\mathbf = \mathbf + \mathbf\ d \quad d\in\mathbb where \mathbf is a unit vector in the direction of the line, \mathbf is a point on the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray Tracing (graphics)
In 3D computer graphics, ray tracing is a technique for modeling Light transport theory, light transport for use in a wide variety of Rendering (computer graphics), rendering algorithms for generating digital image, digital images. On a spectrum of Computation time, computational cost and visual fidelity, ray tracing-based rendering techniques, such as ray casting, #Recursive ray tracing algorithm, recursive ray tracing, Distributed ray tracing, distribution ray tracing, photon mapping and path tracing, are generally slower and higher fidelity than scanline rendering methods. Thus, ray tracing was first deployed in applications where taking a relatively long time to render could be tolerated, such as still computer-generated imagery, CGI images, and film and television visual effects (VFX), but was less suited to real-time computer graphics, real-time applications such as video games, where Frame rate, speed is critical in rendering each Film frame, frame. Since 2018, however, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Equation
In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant coefficient'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the quadratic function on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evident (f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
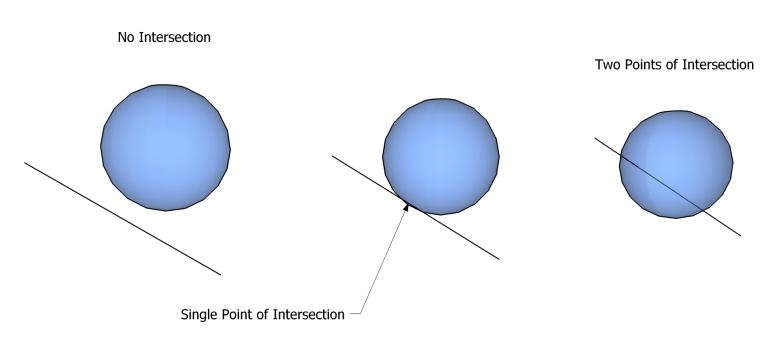
Line–sphere Intersection
In analytic geometry, a line and a sphere can intersect in three ways: # No intersection at all # Intersection in exactly one point # Intersection in two points. Methods for distinguishing these cases, and determining the coordinates for the points in the latter cases, are useful in a number of circumstances. For example, it is a common calculation to perform during ray tracing. Calculation using vectors in 3D In vector notation, the equations are as follows: Equation for a sphere :\left\Vert \mathbf - \mathbf \right\Vert^2=r^2 :*\mathbf : points on the sphere :*\mathbf : center point :*r : radius of the sphere Equation for a line starting at \mathbf :\mathbf=\mathbf + d\mathbf :*\mathbf : points on the line :*\mathbf : origin of the line :*d : distance from the origin of the line :*\mathbf : direction of line (a non-zero vector) Searching for points that are on the line and on the sphere means combining the equations and solving for d, involving the dot product of vector ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Modeling International
Shape Modeling International (SMI), also known as ''International Conference on Shape Modeling and Applications'' is an annual symposium whose goal is to promote the dissemination of new mathematical theories and novel computational techniques for modeling, simulating, and processing digital shape representations. Initiated in 1997 by Tosyiasu L. Kunii and Bianca Falcidieno, the symposium became an annual event in 2001 after its merge with the Eurographics / ACM SIGGRAPH Workshop on Implicit Surfaces. The venue of the symposium rotates in turn among Asia, Europe and America. Overview Since 2009, proceedings of SMI are published by Elsevier as a special issue of the '' Computers & Graphics'' journal. Proceedings until the year 2010 are available at DPLP, computer.org, and IEEE Explore.https://ieeexplore.ieee.org/xpl/conhome/1000664/all-proceedings See also *Symposium on Geometry Processing *SIGGRAPH *Solid modeling Solid modeling (or solid modelling) is a consistent set of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersection (geometry)
In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point (sometimes called a '' vertex'') or does not exist (if the lines are parallel). Other types of geometric intersection include: * Line–plane intersection * Line–sphere intersection * Intersection of a polyhedron with a line * Line segment intersection * Intersection curve Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |