|
Kanakanahalli Ramachandra
Kanakanahalli Ramachandra (18 August 1933 – 17 January 2011) was an Indian mathematician working in both analytic number theory and algebraic number theory. Early career Ramachandra went to the Tata Institute of Fundamental Research (TIFR), Bombay, for his graduate studies in 1958. He obtained his PhD from University of Mumbai in 1965; his doctorate was guided by K. G. Ramanathan. Later career Between the years 1965 and 1995 he worked at the Tata Institute of Fundamental Research and after retirement joined the National Institute of Advanced Studies, Bangalore where he worked till 2011, the year he died. During the course of his lifetime, he published over 200 articles, of which over 170 have been catalogued by Mathematical Reviews. His work was primarily in the area of prime number theory, working on the Riemann zeta function and allied functions. Apart from prime number theory, he made substantial contributions to the theory of transcendental number theory, in which he is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mandya
Mandya is a city in the state of Karnataka. It is the headquarter of Mandya district, Sugar factories contribute to the major economic output. It is also called Sugar City (Kannada: ''Sakkare Nagara'') because sugarcane is a major crop grown here. The district offices are located here. The city has been divided into 35 wards of the Mandya City Municipal Council. History Mandya celebrated its 75th year anniversary (''Amrutha Mahothsava'') in 2015. The KRS dam was built by Krishna Raja Wadiyar IV and M. Visvesvaraya in Mandya, opening in 1932. Mandya is home to a number of historically important sites. In 2016, Archaeological Survey of India (ASI) excavated another statue of Bahubali, a much revered figure among Jains. He was the son of Adinath, the first tirthankara of Jainism, and the younger brother of Bharata Chakravartin, identified with the 3rd – 9th centuries in Arthipura, Mandya district. The excavation is expected to be completed by 2018. The Archaeo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that many mathematicians consider th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2011 Deaths
This is a list of lists of deaths of notable people, organized by year. New deaths articles are added to their respective month (e.g., Deaths in ) and then linked below. 2025 2024 2023 2022 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996 1995 1994 1993 1992 1991 1990 1989 1988 1987 1986 Earlier years ''Deaths in years earlier than this can usually be found in the main articles of the years.'' See also * Lists of deaths by day * Deaths by year (category) {{DEFAULTSORT:deaths by year ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1933 Births
Events January * January 11 – Australian aviator Sir Charles Kingsford Smith makes the first commercial flight between Australia and New Zealand. * January 17 – The United States Congress votes in favour of Philippines independence, against the wishes of U.S. President Herbert Hoover. * January 28 – "Pakistan Declaration": Choudhry Rahmat Ali publishes (in Cambridge, UK) a pamphlet entitled ''Now or Never; Are We to Live or Perish Forever?'', in which he calls for the creation of a Muslim state in northwest India that he calls "Pakistan, Pakstan"; this influences the Pakistan Movement. * January 30 ** Nazi Party leader Adolf Hitler is appointed Chancellor of Germany (German Reich), Chancellor of Germany by President of Germany Paul von Hindenburg. ** Édouard Daladier forms a government in France in succession to Joseph Paul-Boncour. He is succeeded on October 26 by Albert Sarraut and on November 26 by Camille Chautemps. February * February 1 – Adolf Hitle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
21st-century Indian Mathematicians
File:1st century collage.png, From top left, clockwise: Jesus is crucified by Roman authorities in Judaea (17th century painting). Four different men ( Galba, Otho, Vitellius, and Vespasian) claim the title of Emperor within the span of a year; The Great Fire of Rome (18th-century painting) sees the destruction of two-thirds of the city, precipitating the empire's first persecution against Christians, who are blamed for the disaster; The Roman Colosseum is built and holds its inaugural games; Roman forces besiege Jerusalem during the First Jewish–Roman War (19th-century painting); The Trưng sisters lead a rebellion against the Chinese Han dynasty (anachronistic depiction); Boudica, queen of the British Iceni leads a rebellion against Rome (19th-century statue); Knife-shaped coin of the Xin dynasty., 335px rect 30 30 737 1077 Crucifixion of Jesus rect 767 30 1815 1077 Year of the Four Emperors rect 1846 30 3223 1077 Great Fire of Rome rect 30 1108 1106 2155 Boudican re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
People From Mandya
The term "the people" refers to the public or common mass of people of a polity. As such it is a concept of human rights law, international law as well as constitutional law, particularly used for claims of popular sovereignty. In contrast, a people is any plurality of persons considered as a whole. Used in politics and law, the term "a people" refers to the collective or community of an ethnic group or nation. Concepts Legal Chapter One, Article One of the Charter of the United Nations states that "peoples" have the right to self-determination. Though the mere status as peoples and the right to self-determination, as for example in the case of Indigenous peoples (''peoples'', as in all groups of indigenous people, not merely all indigenous persons as in ''indigenous people''), does not automatically provide for independent sovereignty and therefore secession. Indeed, judge Ivor Jennings identified the inherent problems in the right of "peoples" to self-determination, as i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hardy–Ramanujan Journal
The ''Hardy–Ramanujan Journal'' is a mathematics journal covering prime numbers, Diophantine equations, and transcendental numbers. It is named for G. H. Hardy and Srinivasa Ramanujan. Together with the '' Ramanujan Journal'' and the ''Journal of the Ramanujan Mathematical Society'', it is one of three journals named after Ramanujan. It was established in 1978 by R. Balasubramanian and K. Ramachandra and is published once a year on Ramanujan's birthday December 22. It is indexed in MathSciNet.Journal Information for "Hardy-Ramanujan Journal" MathSciNet
MathSciNet is a searchable online bibliographic database created by the American Mat ...
[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Serge Lang
Serge Lang (; May 19, 1927 – September 12, 2005) was a French-American mathematician and activist who taught at Yale University for most of his career. He is known for his work in number theory and for his mathematics textbooks, including the influential ''Algebra''. He received the Frank Nelson Cole Prize in 1960 and was a member of the Bourbaki group. As an activist, Lang campaigned against the Vietnam War, and also successfully fought against the nomination of the political scientist Samuel P. Huntington to the National Academies of Science. Later in his life, Lang was an HIV/AIDS denialist. He claimed that HIV had not been proven to cause AIDS and protested Yale's research into HIV/AIDS. Early life Lang was born in Saint-Germain-en-Laye, close to Paris, in 1927. He had a twin brother who became a basketball coach and a sister who became an actress. Lang moved with his family to California as a teenager, where he graduated in 1943 from Beverly Hills High School. Afte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
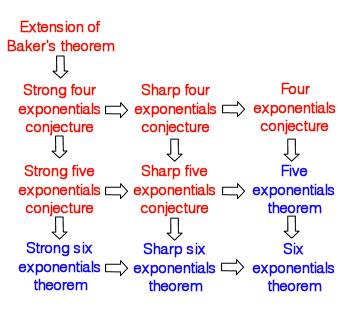
Six Exponentials Theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of six exponentials. Statement : If x_1, x_2, x_3 are three complex numbers that are linearly independent over the rational numbers, and y_1, y_2 are two complex numbers that are also linearly independent over the rational numbers, then at least one of the following numbers is transcendental: e^, e^, e^, e^, e^, e^. The theorem can be stated in terms of logarithms by introducing the set ''L'' of logarithms of algebraic numbers: :\mathcal=\. The theorem then says that if \lambda_ are elements of ''L'' for i = 1,2, j = 1,2,3 such that \lambda_, \lambda_, \lambda_ are linearly independent over the rational numbers, and λ11 and λ21 are also linearly independent over the rational numbers, then the matrix :M=\begin\lambda_&\lambda_&\lambda_ \\ \lambda_&\lambda_&\lambda_\end ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Number Theory
Transcendental number theory is a branch of number theory that investigates transcendental numbers (numbers that are not solutions of any polynomial equation with rational coefficients), in both qualitative and quantitative ways. Transcendence The fundamental theorem of algebra tells us that if we have a non-constant polynomial with rational coefficients (or equivalently, by clearing denominators, with integer coefficients) then that polynomial will have a root in the complex numbers. That is, for any non-constant polynomial P with rational coefficients there will be a complex number \alpha such that P(\alpha)=0. Transcendence theory is concerned with the converse question: given a complex number \alpha, is there a polynomial P with rational coefficients such that P(\alpha)=0? If no such polynomial exists then the number is called transcendental. More generally the theory deals with algebraic independence of numbers. A set of numbers is called algebraically independen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Reviews
''Mathematical Reviews'' is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet, which contains an electronic version of ''Mathematical Reviews''. Reviews Mathematical Reviews was founded by Otto E. Neugebauer in 1940 as an alternative to the German journal '' Zentralblatt für Mathematik'', which Neugebauer had also founded a decade earlier, but which under the Nazis had begun censoring reviews by and of Jewish mathematicians. The goal of the new journal was to give reviews of every mathematical research publication. As of November 2007, the ''Mathematical Reviews'' database contained information on over 2.2 million articles. The authors of reviews are volunteers, usually chosen by the editors because of some expertise in the area of the articl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |