|
Johnson–Lindenstrauss Lemma
In mathematics, the Johnson–Lindenstrauss lemma is a result named after William B. Johnson and Joram Lindenstrauss concerning low-distortion embeddings of points from high-dimensional into low-dimensional Euclidean space. The lemma states that a set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved. In the classical proof of the lemma, the embedding is a random orthogonal projection. The lemma has applications in compressed sensing, manifold learning, dimensionality reduction, graph embedding, and natural language processing. Much of the data stored and manipulated on computers, including text and images, can be represented as points in a high-dimensional space (see vector space model for the case of text). However, the essential algorithms for working with such data tend to become bogged down very quickly as dimension increases. It is therefore desirable to reduce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William B
William is a masculine given name of Germanic origin. It became popular in England after the Norman conquest in 1066,All Things William"Meaning & Origin of the Name"/ref> and remained so throughout the Middle Ages and into the modern era. It is sometimes abbreviated "Wm." Shortened familiar versions in English include Will or Wil, Wills, Willy, Willie, Bill, Billie, and Billy. A common Irish form is Liam. Scottish diminutives include Wull, Willie or Wullie (as in Oor Wullie). Female forms include Willa, Willemina, Wilma and Wilhelmina. Etymology William is related to the German given name ''Wilhelm''. Both ultimately descend from Proto-Germanic ''*Wiljahelmaz'', with a direct cognate also in the Old Norse name ''Vilhjalmr'' and a West Germanic borrowing into Medieval Latin ''Willelmus''. The Proto-Germanic name is a compound of *''wiljô'' "will, wish, desire" and *''helmaz'' "helm, helmet".Hanks, Hardcastle and Hodges, ''Oxford Dictionary of First Names'', Oxfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concentration Of Measure
In mathematics, concentration of measure (about a median) is a principle that is applied in measure theory, probability and combinatorics, and has consequences for other fields such as Banach space theory. Informally, it states that "A random variable that depends in a Lipschitz way on many independent variables (but not too much on any of them) is essentially constant". The concentration of measure phenomenon was put forth in the early 1970s by Vitali Milman in his works on the local theory of Banach spaces, extending an idea going back to the work of Paul Lévy. It was further developed in the works of Milman and Gromov, Maurey, Pisier, Schechtman, Talagrand, Ledoux, and others. The general setting Let (X, d) be a metric space with a measure \mu on the Borel sets with \mu(X) = 1. Let :\alpha(\varepsilon) = \sup \left\, where :A_\varepsilon = \left\ is the \varepsilon-''extension'' (also called \varepsilon-fattening in the context of the Hausdorff distance) of a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Kernel
In machine learning, the polynomial kernel is a kernel function commonly used with support vector machines (SVMs) and other Kernel trick, kernelized models, that represents the similarity of vectors (training samples) in a feature space over polynomials of the original variables, allowing learning of non-linear models. Intuitively, the polynomial kernel looks not only at the given features of input samples to determine their similarity, but also combinations of these. In the context of regression analysis, such combinations are known as interaction features. The (implicit) feature space of a polynomial kernel is equivalent to that of polynomial regression, but without the combinatorial blowup in the number of parameters to be learned. When the input features are binary-valued (booleans), then the features correspond to logical conjunctions of input features.Yoav Goldberg and Michael Elhadad (2008). splitSVM: Fast, Space-Efficient, non-Heuristic, Polynomial Kernel Computation for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hadamard Product (matrices)
In mathematics, the Hadamard product (also known as the element-wise product, entrywise product or Schur product) is a binary operation that takes in two Matrix (mathematics), matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the Matrix multiplication, matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German mathematician Issai Schur. The Hadamard product is associative and Distributive property, distributive. Unlike the matrix product, it is also commutative. Definition For two matrices and of the same dimension , the Hadamard product A \odot B (sometimes A \circ B) is a matrix of the same dimension as the operands, with elements given by :(A \odot B)_ = (A)_ (B)_. For matrices of different dimensions ( and , where or ), the Hadamard product is undefined. An example of the Hadamard product for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
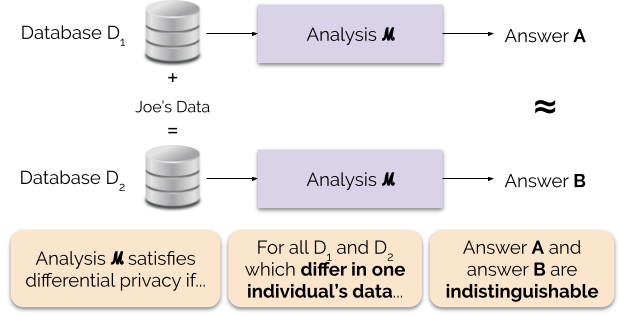
Differential Privacy
Differential privacy (DP) is a mathematically rigorous framework for releasing statistical information about datasets while protecting the privacy of individual data subjects. It enables a data holder to share aggregate patterns of the group while limiting information that is leaked about specific individuals. This is done by injecting carefully calibrated noise into statistical computations such that the utility of the statistic is preserved while provably limiting what can be inferred about any individual in the dataset. Another way to describe differential privacy is as a constraint on the algorithms used to publish aggregate information about a statistical database which limits the disclosure of private information of records in the database. For example, differentially private algorithms are used by some government agencies to publish demographic information or other statistical aggregates while ensuring confidentiality of survey responses, and by companies to collect informa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Antenna Array
Digital antenna array (DAA) is a smart antenna with multi channels digital beamforming, usually by using fast Fourier transform (FFT). The development and practical realization of digital antenna arrays theory started in 1962 under the guidance of Vladimir Varyukhin (USSR). History The history of the DAA was started to emerge as a theory of multichannel analysis in the 1920s.Slyusar V. I. Origins of the Digital Antenna Array Theory.// International Conference on Antenna Theory and Techniques, 24–27 May 2017, Kyiv, Ukraine. – Pp. 199 - 20/ref> In the 1940s this theory evolved to the theory of three-channel antenna analyzers. The implementation of effective signal processing in radars by the end of the 1950s predetermined the use of electronic computers in this field. In 1957, Ben S. Meltont and Leslie F. Bailey published article regarding using algebraic operations for signal processing with the help of electronic circuits or analog computer. Three years after in 1960 th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radar
Radar is a system that uses radio waves to determine the distance ('' ranging''), direction ( azimuth and elevation angles), and radial velocity of objects relative to the site. It is a radiodetermination method used to detect and track aircraft, ships, spacecraft, guided missiles, motor vehicles, map weather formations, and terrain. The term ''RADAR'' was coined in 1940 by the United States Navy as an acronym for "radio detection and ranging". The term ''radar'' has since entered English and other languages as an anacronym, a common noun, losing all capitalization. A radar system consists of a transmitter producing electromagnetic waves in the radio or microwave domain, a transmitting antenna, a receiving antenna (often the same antenna is used for transmitting and receiving) and a receiver and processor to determine properties of the objects. Radio waves (pulsed or continuous) from the transmitter reflect off the objects and return to the receiver, giving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
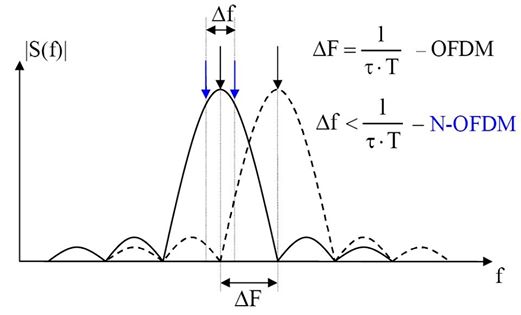
Vadym Slyusar
Vadym Slyusar (born 15 October 1964, vil. Kolotii, Reshetylivka Raion, Poltava region, Ukraine) is a Soviet and Ukrainian scientist, Professor, Doctor of Technical Sciences, Honored Scientist and Technician of Ukraine, founder of tensor-matrix theory of digital antenna arrays (DAAs), N-OFDM and other theories in fields of radar systems, smart antennas for wireless communications and digital beamforming. Scientific results N-OFDM theory In 1992 Vadym Slyusar patented the 1st optimal demodulation method for N-OFDM signals after Fast Fourier transform (FFT).RU2054684 (C1) G01R 23/16. Amplitude-frequency response measurement technique// Slyusar V. – Appl. Number SU 19925055759, Priority Data: 19920722. – Official Publication Data: 1996-02-2/ref> From this patent was started the history of N-OFDM signals theory. In this regard, W. Kozek and A. F. Molisch wrote in 1998 about N-OFDM signals with the sub-carrier spacing \alpha before the conference paper of I. Darwazeh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Khatri–Rao Product
In mathematics, the Khatri–Rao product or block Kronecker product of two partitioned matrix, partitioned matrices \mathbf and \mathbf is defined as : \mathbf \ast \mathbf = \left(\mathbf_ \otimes \mathbf_\right)_ in which the ''ij''-th block is the sized Kronecker product of the corresponding blocks of A and B, assuming the number of row and column partitions of both Matrix (mathematics), matrices is equal. The size of the product is then . For example, if A and B both are partitioned matrices e.g.: : \mathbf = \left[ \begin \mathbf_ & \mathbf_ \\ \hline \mathbf_ & \mathbf_ \end \right] = \left[ \begin 1 & 2 & 3 \\ 4 & 5 & 6 \\ \hline 7 & 8 & 9 \end \right] ,\quad \mathbf = \left[ \begin \mathbf_ & \mathbf_ \\ \hline \mathbf_ & \mathbf_ \end \right] = \left[ \begin 1 & 4 & 7 \\ \hline 2 & 5 & 8 \\ 3 & 6 & 9 \end \right] , we obtain: : \mathbf \ast \mathbf = \left[ \begin \mathbf_ \otimes \mathbf_ & \mathbf_ \otimes \mathbf_ \\ \hline \mathbf_ \otimes \mathbf_ & \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The ACM
The ''Journal of the ACM'' (''JACM'') is a peer-reviewed scientific journal covering computer science in general, especially theoretical aspects. It is an official journal of the Association for Computing Machinery. Its current editor-in-chief is Venkatesan Guruswami. The journal was established in 1954 and "computer scientists universally hold the ''Journal of the ACM'' in high esteem". See also * ''Communications of the ACM ''Communications of the ACM'' (''CACM'') is the monthly journal of the Association for Computing Machinery (ACM). History It was established in 1958, with Saul Rosen as its first managing editor. It is sent to all ACM members. Articles are i ...'' References External links * {{DEFAULTSORT:Journal Of The Acm Academic journals established in 1954 Computer science journals Association for Computing Machinery academic journals Bimonthly journals English-language journals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernard Chazelle
Bernard Chazelle (born November 5, 1955) is a French computer scientist. He is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he is known for his study of algorithms, such as linear-time triangulation of a simple polygon, as well as major complexity results, such as lower bound techniques based on discrepancy theory. He is also known for his invention of the soft heap data structure and the most asymptotically efficient known deterministic algorithm for finding minimum spanning trees. Early life Chazelle was born in Clamart, France, the son of Marie-Claire (née Blanc) and Jean Chazelle. He grew up in Paris, France, where he received his bachelor's degree and master's degree in applied mathematics at the École des mines de Paris in 1977. Then, at the age of 21, he attended Yale University in the United States, where he received his PhD in computer science in 1980 under the supervision of David ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sub-Gaussian Distribution
In probability theory, a subgaussian distribution, the distribution of a subgaussian random variable, is a probability distribution with strong tail decay. More specifically, the tails of a subgaussian distribution are dominated by (i.e. decay at least as fast as) the tails of a Gaussian distribution, Gaussian. This property gives subgaussian distributions their name. Often in analysis, we divide an object (such as a random variable) into two parts, a central bulk and a distant tail, then analyze each separately. In probability, this division usually goes like "Everything interesting happens near the center. The tail event is so rare, we may safely ignore that." Subgaussian distributions are worthy of study, because the gaussian distribution is well-understood, and so we can give sharp bounds on the rarity of the tail event. Similarly, the Subexponential distribution (light-tailed), subexponential distributions are also worthy of study. Formally, the probability distribution of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |