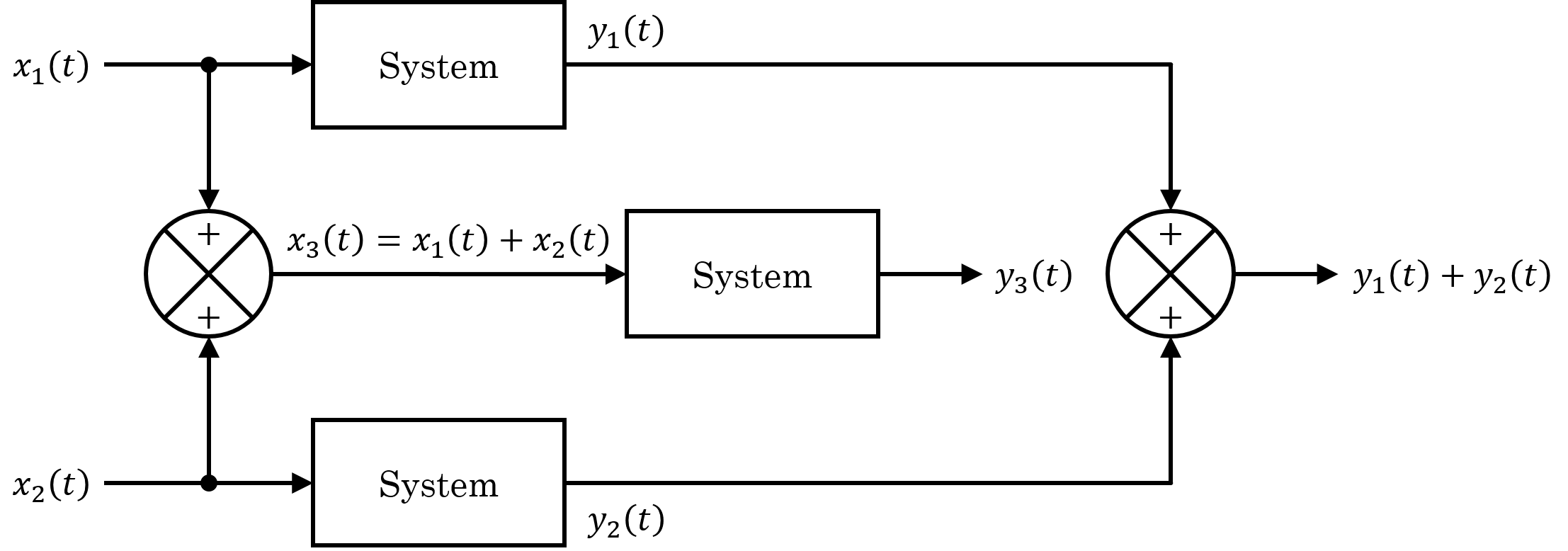
|
Iterative Rational Krylov Algorithm
The iterative rational Krylov algorithm (IRKA), is an iterative algorithm, useful for model order reduction (MOR) of single-input single-output (SISO) linear time-invariant dynamical systems. At each iteration, IRKA does an Hermite type interpolation of the original system transfer function. Each interpolation requires solving r shifted pairs of linear systems, each of size n \times n; where n is the original system order, and r is the desired reduced model order (usually r \ll n). The algorithm was first introduced by Gugercin, Antoulas and Beattie in 2008. It is based on a first order necessary optimality condition, initially investigated by Meier and Luenberger in 1967. The first convergence proof of IRKA was given by Flagg, Beattie and Gugercin in 2012, for a particular kind of systems. MOR as an optimization problem Consider a SISO linear time-invariant dynamical system, with input v(t), and output y(t): : \begin \dot(t) = A x(t) + b v(t)\\ y(t) = c^T x(t) \end \qquad A \i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Order Reduction
Model order reduction (MOR) is a technique for reducing the computational complexity of mathematical models in numerical simulations. As such it is closely related to the concept of metamodeling, with applications in all areas of mathematical modelling. Overview Many modern mathematical models of real-life processes pose challenges when used in numerical simulations, due to complexity and large size (dimension). Model order reduction aims to lower the computational complexity of such problems, for example, in simulations of large-scale dynamical systems and control systems. By a reduction of the model's associated state space dimension or degrees of freedom, an approximation to the original model is computed which is commonly referred to as a reduced order model. Reduced order models are useful in settings where it is often unfeasible to perform numerical simulations using the complete full order model. This can be due to limitations in computational resources or the requirement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-input Single-output
In control engineering, a single-input and single-output (SISO) system is a simple single variable control system with one input and one output. In radio it is the use of only one antenna both in the transmitter and receiver. Details SISO systems are typically less complex than multiple-input multiple-output (MIMO) systems. Usually, it is also easier to make order of magnitude or trending predictions "on the fly" or "back of the envelope". MIMO systems have too many interactions for most of us to trace through them quickly, thoroughly, and effectively in our heads. Frequency domain techniques for analysis and controller design dominate SISO control system theory. Bode plot, Nyquist stability criterion, Nichols plot, and root locus are the usual tools for SISO system analysis. Controllers can be designed through the polynomial design, root locus design methods to name just two of the more popular. Often SISO controllers will be PI, PID, or lead-lag. See also * Control theory * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, that maps an input, as a function of to an output, a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear combin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform that converts a function of a real variable (usually t, in the ''time domain'') to a function of a complex variable s (in the complex frequency domain, also known as ''s''-domain, or s-plane). The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions ''f'', the Laplace transform is the integral \mathcal\(s) = \int_0^\infty f(t)e^ \, dt. History The Laplace transform is named after mathematician and astronomer Pierre-Simon, marquis de Laplace, who used a similar transform in his work on probability theory. Laplace wrote extensively about the use of generating functions in ''Essai philosophique sur les probabilités'' (1814), and the integral form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a mathematical function that theoretically models the system's output for each possible input. They are widely used in electronics and control systems. In some simple cases, this function is a two-dimensional graph of an independent scalar input versus the dependent scalar output, called a transfer curve or characteristic curve. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. The dimensions and units of the transfer function model the output response of the device for a range of possible inputs. For example, the transfer function of a two-port electronic circuit like an amplifier might be a two-dimensional graph of the scalar voltage at the output as a function of the scalar voltage applied to the input; the transfer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, optimization includes finding "best available" values of some objective function given a def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric field, electric and magnetic fields are generated by electric charge, charges, electric current, currents, and changes of the fields.''Electric'' and ''magnetic'' fields, according to the theory of relativity, are the components of a single electromagnetic field. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiple-input Multiple-output
In radio, multiple-input and multiple-output, or MIMO (), is a method for multiplying the capacity of a radio link using multiple transmission and receiving antennas to exploit multipath propagation. MIMO has become an essential element of wireless communication standards including IEEE 802.11n (Wi-Fi 4), IEEE 802.11ac (Wi-Fi 5), HSPA+ (3G), WiMAX, and LTE (telecommunication), Long Term Evolution (LTE). More recently, MIMO has been applied to power-line communication for three-wire installations as part of the ITU G.hn standard and of the HomePlug AV2 specification. At one time, in wireless the term "MIMO" referred to the use of multiple antennas at the transmitter and the receiver. In modern usage, "MIMO" specifically refers to a class of techniques for sending and receiving more than one data signal simultaneously over the same radio channel by exploiting multipath propagation. Additionally, modern MIMO usage often refers to multiple data signals sent to different receiver ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Order Reduction
Model order reduction (MOR) is a technique for reducing the computational complexity of mathematical models in numerical simulations. As such it is closely related to the concept of metamodeling, with applications in all areas of mathematical modelling. Overview Many modern mathematical models of real-life processes pose challenges when used in numerical simulations, due to complexity and large size (dimension). Model order reduction aims to lower the computational complexity of such problems, for example, in simulations of large-scale dynamical systems and control systems. By a reduction of the model's associated state space dimension or degrees of freedom, an approximation to the original model is computed which is commonly referred to as a reduced order model. Reduced order models are useful in settings where it is often unfeasible to perform numerical simulations using the complete full order model. This can be due to limitations in computational resources or the requirement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |