|
Interacting Particle System
In probability theory, an interacting particle system (IPS) is a stochastic process (X(t))_ on some configuration space \Omega= S^G given by a site space, a countably-infinite-order graph G and a local state space, a compact metric space S . More precisely IPS are continuous-time Markov jump processes describing the collective behavior of stochastically interacting components. IPS are the continuous-time analogue of stochastic cellular automata. Among the main examples are the voter model, the contact process, the asymmetric simple exclusion process (ASEP), the Glauber dynamics and in particular the stochastic Ising model. IPS are usually defined via their Markov generator giving rise to a unique Markov process using Markov semigroups and the Hille-Yosida theorem. The generator again is given via so-called transition rates c_\Lambda(\eta,\xi)>0 where \Lambda\subset G is a finite set of sites and \eta,\xi\in\Omega with \eta_i=\xi_i for all i\notin\Lambda. The rates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ising Model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent Nuclear magnetic moment, magnetic dipole moments of atomic "spins" that can be in one of two states (+1 or −1). The spins are arranged in a Graph (abstract data type), graph, usually a lattice (group), lattice (where the local structure repeats periodically in all directions), allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases.The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition. Though it is a highly simplified model of a magnetic material, the Ising model can sti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Systems Theory
A complex system is a system composed of many components that may interact with one another. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, complex software and electronic systems, social and economic organizations (like cities), an ecosystem, a living cell, and, ultimately, for some authors, the entire universe. The behavior of a complex system is intrinsically difficult to model due to the dependencies, competitions, relationships, and other types of interactions between their parts or between a given system and its environment. Systems that are " complex" have distinct properties that arise from these relationships, such as nonlinearity, emergence, spontaneous order, adaptation, and feedback loops, among others. Because such systems appear in a wide variety of fields, the commonalities among them have become the topic of their independent area of research. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-organization
Self-organization, also called spontaneous order in the social sciences, is a process where some form of overall order and disorder, order arises from local interactions between parts of an initially disordered system. The process can be spontaneous when sufficient energy is available, not needing control by any external agent. It is often triggered by seemingly random Statistical fluctuations, fluctuations, amplified by positive feedback. The resulting organization is wholly decentralized, :wikt:distribute, distributed over all the components of the system. As such, the organization is typically Robustness, robust and able to survive or self-healing material, self-repair substantial perturbation theory, perturbation. Chaos theory discusses self-organization in terms of islands of predictability in a sea of chaotic unpredictability. Self-organization occurs in many physics, physical, chemistry, chemical, biology, biological, robotics, robotic, and cognitive systems. Examples of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Models
Lattice may refer to: Arts and design * Latticework, an ornamental criss-crossed framework, an arrangement of crossing laths or other thin strips of material * Lattice (music), an organized grid model of pitch ratios * Lattice (pastry), an ornamental pattern of crossing strips of pastry Companies * Lattice Engines, a technology company specializing in business applications for marketing and sales * Lattice Group, a former British gas transmission business * Lattice Semiconductor, a US-based integrated circuit manufacturer Science, technology, and mathematics Mathematics * Lattice (group), a repeating arrangement of points ** Lattice (discrete subgroup), a discrete subgroup of a topological group whose quotient carries an invariant finite Borel measure ** Lattice (module), a module over a ring that is embedded in a vector space over a field ** Lattice graph, a graph that can be drawn within a repeating arrangement of points ** Lattice-based cryptography, encryp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas M
Thomas may refer to: People * List of people with given name Thomas * Thomas (name) * Thomas (surname) * Saint Thomas (other) * Thomas Aquinas (1225–1274) Italian Dominican friar, philosopher, and Doctor of the Church * Thomas the Apostle * Thomas (bishop of the East Angles) (fl. 640s–650s), medieval Bishop of the East Angles * Thomas (Archdeacon of Barnstaple) (fl. 1203), Archdeacon of Barnstaple * Thomas, Count of Perche (1195–1217), Count of Perche * Thomas (bishop of Finland) (1248), first known Bishop of Finland * Thomas, Earl of Mar (1330–1377), 14th-century Earl, Aberdeen, Scotland Geography Places in the United States * Thomas, Idaho * Thomas, Illinois * Thomas, Oklahoma * Thomas, Oregon * Thomas, South Dakota * Thomas, Virginia * Thomas, Washington * Thomas, West Virginia * Thomas County (other) * Thomas Township (other) Elsewhere * Thomas Glacier (Greenland) Arts and entertainment * ''Thomas'' (Burton novel), a 196 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rick Durrett
Richard Timothy Durrett is an American mathematician known for his research and books on mathematical probability theory, stochastic processes and their application to mathematical ecology and population genetics. Education and career He received his BS and MS at Emory University in 1972 and 1973 and his Ph.D. at Stanford University in 1976 under advisor Donald Iglehart. From 1976 to 1985 he taught at UCLA. From 1985 until 2010 was on the faculty at Cornell University, where his students included Claudia Neuhauser. Since 2010, Durrett has been a professor at Duke University. He was elected to the United States National Academy of Sciences in 2007. In 2012 he became a fellow of the American Mathematical Society The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, .... Durrett is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Functions
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semigroups
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it. The binary operation of a semigroup is most often denoted multiplicatively (just notation, not necessarily the elementary arithmetic multiplication): , or simply ''xy'', denotes the result of applying the semigroup operation to the ordered pair . Associativity is formally expressed as that for all ''x'', ''y'' and ''z'' in the semigroup. Semigroups may be considered a special case of magmas, where the operation is associative, or as a generalization of groups, without requiring the existence of an identity element or inverses. As in the case of groups or magmas, the semigroup operation need not be commutative, so is not necessarily equal to ; a well-known example of an operation that is associative but non-commutative is matrix multiplication. If the semigroup operation is commutative, then the semigroup is called a ''commutative semigroup'' o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal Generator (stochastic Processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a Feller process (i.e. a continuous-time Markov process satisfying certain regularity conditions) is a Fourier multiplier operator that encodes a great deal of information about the process. The generator is used in evolution equations such as the Kolmogorov backward equation, which describes the evolution of statistics of the process; its ''L''2 Hermitian adjoint is used in evolution equations such as the Fokker–Planck equation, also known as Kolmogorov forward equation, which describes the evolution of the probability density functions of the process. The Kolmogorov forward equation in the notation is just \partial_t \rho = \mathcal A^* \rho, where \rho is the probability density function, and \mathcal A^* is the adjoint of the infinitesimal generator of the underlying stochastic process. The Klein–Kramers equation is a special case of that. Definition General case For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
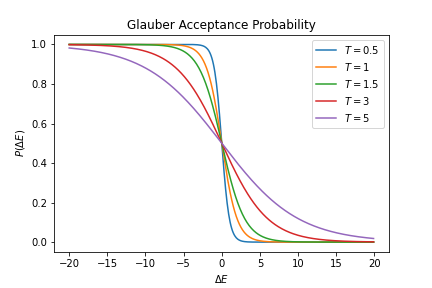
Glauber Dynamics
In statistical physics, Glauber dynamics is a way to simulate the Ising model (a model of magnetism) on a computer. The algorithm is named after Roy J. Glauber. The algorithm The Ising model is an abstract model for the magnetic interaction of neighboring atoms. It is conventionally considered on a two-dimensional square lattice, with magnetic interactions occurring only between nearest neighbors. In this model, each lattice site is given a spin \sigma_ that is either up (+1) or down (-1); the x and y are the grid coordinates. Glauber's algorithm becomes: # Choose a location x,y at random. # Sum the spins of the nearest-neighbors. For a two-D square lattice, there are four: S = \sigma_ + \sigma_ + \sigma_ + \sigma_. # Compute the change in energy if the spin at x, y were to flip. This is given by the Hamiltonian for the Ising model; it is \Delta E = 2\sigma_ S. # Flip the spin with probability given by the Fermi function p(\Delta E) = 1/(1 + e^), where T is the temperature. # Go ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |