|
I-shaped
Many shapes have metaphorical names, i.e., their names are metaphors: these shapes are named after a most common object that has it. For example, "U-shape" is a shape that resembles the letter U, a bell-shaped curve has the shape of the vertical cross section of a bell, etc. These terms may variously refer to objects, their cross sections or projections. Types of shapes Some of these names are "classical terms", i.e., words of Latin or Ancient Greek etymology. Others are English language constructs (although the base words may have non-English etymology). In some disciplines, where shapes of subjects in question are a very important consideration, the shape naming may be quite elaborate, see, e.g., the taxonomy of shapes of plant leaves in botany. * Astroid * Aquiline, shaped like an eagle's beak (as in a Roman nose) * Bell-shaped curve * Biconic shape, a shape in a way opposite to the hourglass: it is based on two oppositely oriented cones or truncated cones with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian 2d
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below. There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymous adjective ''Gaussian'' is pronounced . Mathematics Algebra and linear algebra Geometry and differential geometry Number theory Cyclotomic fields * Gaussian period * Gaussian rational * Gauss sum, an exponential sum over Dirichlet characters ** Elliptic Gauss sum, an analog of a Gauss sum ** Quadratic Gauss sum Analysis, numerical analysis Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ..., vector calculus and calculus of variations Complex analysis and convex analysis * Gauss–Lucas theorem * Gau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Botany
Botany, also called plant science, is the branch of natural science and biology studying plants, especially Plant anatomy, their anatomy, Plant taxonomy, taxonomy, and Plant ecology, ecology. A botanist or plant scientist is a scientist who specialises in this field. "Plant" and "botany" may be defined more narrowly to include only land plants and their study, which is also known as phytology. Phytologists or botanists (in the strict sense) study approximately 410,000 species of Embryophyte, land plants, including some 391,000 species of vascular plants (of which approximately 369,000 are flowering plants) and approximately 20,000 bryophytes. Botany originated as history of herbalism#Prehistory, prehistoric herbalism to identify and later cultivate plants that were edible, poisonous, and medicinal, making it one of the first endeavours of human investigation. Medieval physic gardens, often attached to Monastery, monasteries, contained plants possibly having medicinal benefit. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Egg-shaped
An oval () is a closed curve in a plane (geometry), plane which resembles the outline of an egg. The term is not very specific, but in some areas of mathematics (projective geometry, technical drawing, etc.), it is given a more precise definition, which may include either one or two axes of symmetry of an ellipse. In common English, the term is used in a broader sense: any shape which reminds one of an egg. The three-dimensional version of an oval is called an ovoid. Oval in geometry The term oval when used to describe curves in geometry is not well-defined, except in the context of projective geometry. Many distinct curves are commonly called ovals or are said to have an "oval shape". Generally, to be called an oval, a Plane (geometry), plane curve should ''resemble'' the outline of an egg (food), egg or an ellipse. In particular, these are common traits of ovals: * they are curve, differentiable (smooth-looking), curve, simple (not self-intersecting), Convex curve, convex, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pine Cone
A conifer cone, or in formal botanical usage a strobilus, : strobili, is a seed-bearing organ on gymnosperm plants, especially in conifers and cycads. They are usually woody and variously conic, cylindrical, ovoid, to globular, and have scales and bracts arranged around a central axis, but can be fleshy and berry-like. The cone of Pinophyta (conifer clade) contains the reproductive structures. The woody cone is the female cone, which produces seeds. The male cone, which produces pollen, is usually ephemeral and much less conspicuous even at full maturity. The name "cone" derives from Greek ''konos'' (pine cone), which also gave name to the geometric cone. The individual plates of a cone are known as ''scales''. In conifers where the cone develops over more than one year (such as pines), the first year's growth of a seed scale on the cone, showing up as a protuberance at the end of the two-year-old scale, is called an ''umbo'', while the second year's growth is called the '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
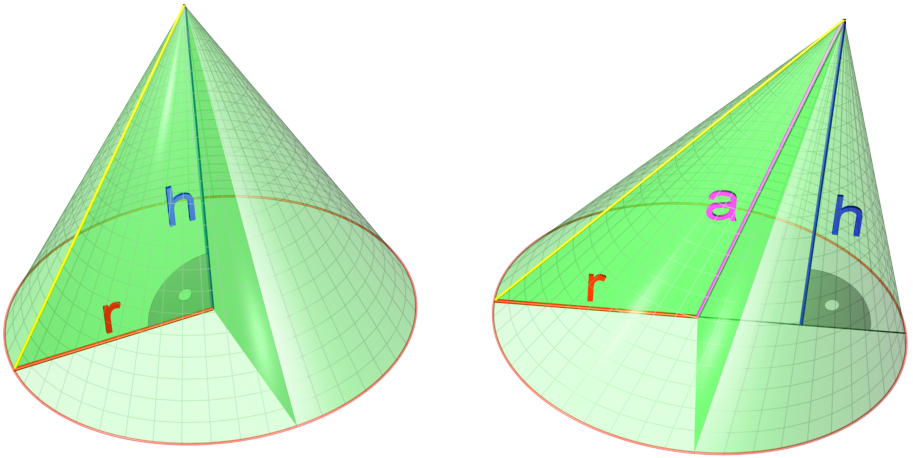
Cone (geometry)
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterfly Curve (algebraic)
In mathematics, the algebraic butterfly curve is a plane algebraic curve of degree six, given by the equation :x^6 + y^6 = x^2. The butterfly curve has a single singularity with delta invariant three, which means it is a curve of genus seven. The only plane curves of genus seven are singular, since seven is not a triangular number, and the minimum degree for such a curve is six. The butterfly curve has branching number and multiplicity two, and hence the singularity link has two components, pictured at right. The area of the algebraic butterfly curve is given by (with gamma function \Gamma) :4 \cdot \int_0^1 (x^2 - x^6)^ dx = \frac \approx 2.804, and its arc length Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the ... ''s'' by :s \approx 9.017. See also * Butterfly curve (t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bow Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Twenty-eight bi-tangents * Three ordinary double points. One may also consider quartic curves over oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ramjet
A ramjet is a form of airbreathing jet engine that requires forward motion of the engine to provide air for combustion. Ramjets work most efficiently at supersonic speeds around and can operate up to . Ramjets can be particularly appropriate in uses requiring a compact mechanism for high-speed, such as missiles. Weapons designers are investigating ramjet technology for use in artillery shells to increase range; a 120 mm ramjet-assisted mortar shell is thought to be able to travel . They have been used, though not efficiently, as tip jets on the ends of helicopter rotors. History France Cyrano de Bergerac ''L'Autre Monde: ou les États et Empires de la Lune ( Comical History of the States and Empires of the Moon)'' (1657) was the first of three satirical novels written by Cyrano de Bergerac that are considered among the first science fiction stories. Arthur C Clarke credited this book with conceiving the ramjet, and as the first fictional example of rocket-powered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inlet Cone
Inlet cones (sometimes called shock cones or inlet centerbodies) are a component of some supersonic aircraft and missiles. They are primarily used on ramjets, such as the D-21 Tagboard and Lockheed X-7. Some turbojet aircraft including the Su-7, MiG-21, English Electric Lightning, and SR-71 also use an inlet cone. Purpose An inlet cone, as part of an Oswatitsch-type inlet used on a supersonic aircraft or missile, is the 3D-surface on which supersonic ram compression for a gas turbine engine or ramjet combustor takes place through oblique shock waves. Slowing the air to low supersonic speeds using a cone minimizes loss in total pressure (increases pressure recovery). Also, the cone, together with the inlet cowl lip, determine the area which regulates the flow entering the inlet. If the flow is more than that required by the engine then shock position instability (buzz) can occur. If less than that required then the pressure recovery is lower which reduces engine thrust. An in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Reentry
Atmospheric entry (sometimes listed as Vimpact or Ventry) is the movement of an object from outer space into and through the gases of an atmosphere of a planet, dwarf planet, or natural satellite. Atmospheric entry may be ''uncontrolled entry,'' as in the entry of astronomical objects, space debris, or bolides. It may be ''controlled entry'' (or ''reentry'') of a spacecraft that can be navigated or follow a predetermined course. Methods for controlled atmospheric ''entry, descent, and landing'' of spacecraft are collectively termed as ''EDL''. Objects entering an atmosphere experience Drag (physics), atmospheric drag, which puts mechanical stress on the object, and aerodynamic heating—caused mostly by compression of the air in front of the object, but also by drag. These forces can cause loss of mass (ablation) or even complete disintegration of smaller objects, and objects with lower compressive strength can explode. Objects have reentered with speeds ranging from 7.8&n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |