|
H. F. Baker
Henry Frederick Baker Royal Society, FRS Royal Society of Edinburgh, FRSE (3 July 1866 – 17 March 1956) was a British mathematician, working mainly in algebraic geometry, but also remembered for contributions to partial differential equations (related to what would become known as solitons), and Lie groups. Early life He was born in Cambridge the son of Henry Baker, a butler, and Sarah Ann Britham. Education He was educated at The Perse School before winning a scholarship to St John's College, Cambridge in October 1884. Baker graduated as Senior Wrangler in 1887, bracketed with 3 others. His doctoral advisor was Arthur Cayley. Career Baker was elected Fellow of St John's in 1888 where he remained for 68 years. In June 1898, he was elected a Fellow of the Royal Society. In 1911, he gave the presidential address to the London Mathematical Society. Baker was one of the mathematicians (along with E. W. Hobson) to whom Srinivasa Ramanujan wrote before G. H. Hardy but his pape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
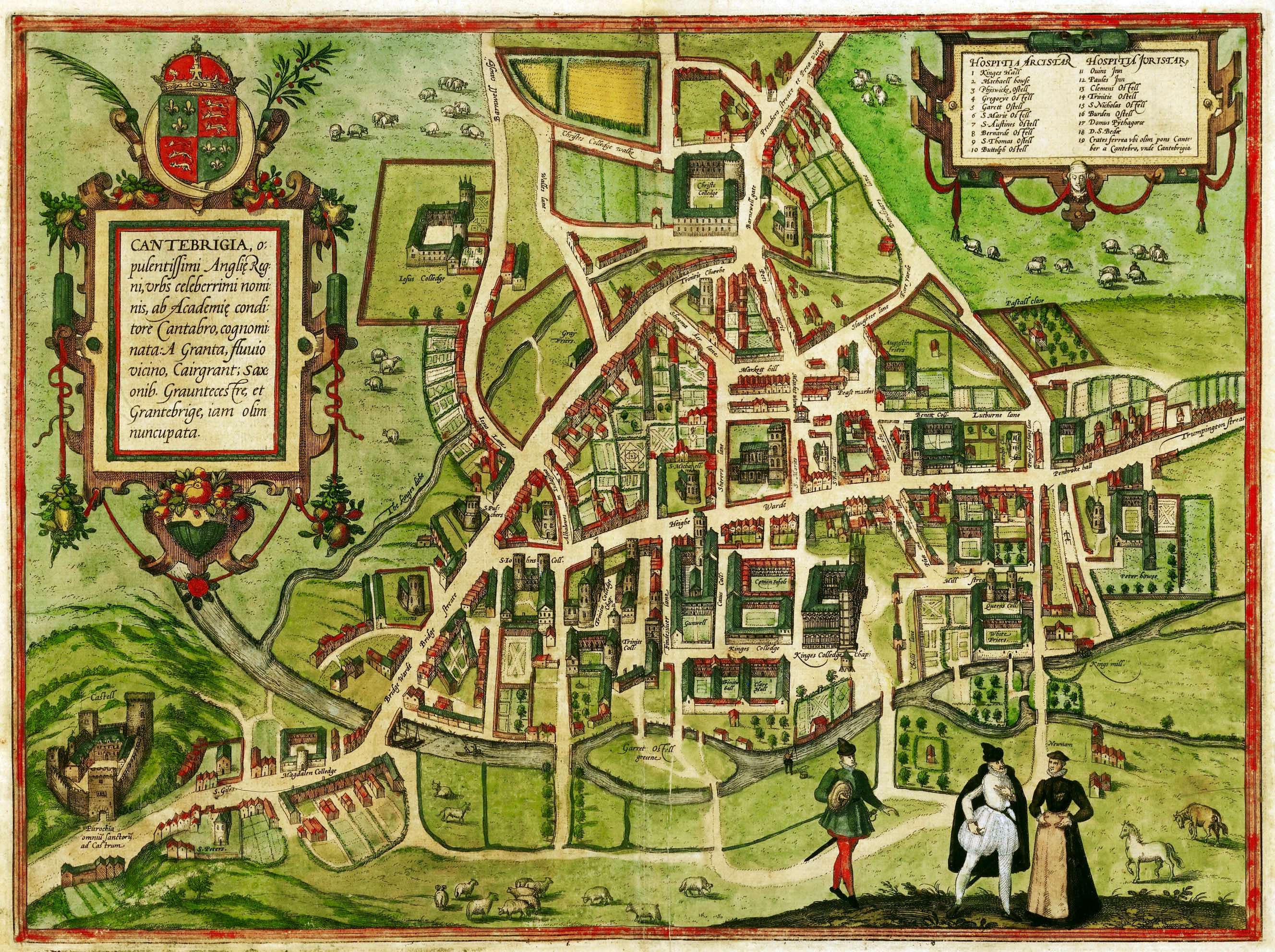
Cambridge
Cambridge ( ) is a List of cities in the United Kingdom, city and non-metropolitan district in the county of Cambridgeshire, England. It is the county town of Cambridgeshire and is located on the River Cam, north of London. As of the 2021 United Kingdom census, the population of the City of Cambridge was 145,700; the population of the wider built-up area (which extends outside the city council area) was 181,137. (2021 census) There is archaeological evidence of settlement in the area as early as the Bronze Age, and Cambridge became an important trading centre during the Roman Britain, Roman and Viking eras. The first Town charter#Municipal charters, town charters were granted in the 12th century, although modern city status was not officially conferred until 1951. The city is well known as the home of the University of Cambridge, which was founded in 1209 and consistently ranks among the best universities in the world. The buildings of the university include King's College Chap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smith's Prize
Smith's Prize was the name of each of two prizes awarded annually to two research students in mathematics and theoretical physics at the University of Cambridge from 1769. Following the reorganization in 1998, they are now awarded under the names Smith-Knight Prize and Rayleigh-Knight Prize. History The Smith Prize fund was founded by bequest of Robert Smith (mathematician), Robert Smith upon his death in 1768, having by his will left £3,500 of South Sea Company stock to the University. Every year two or more junior Bachelor of Arts students who had made the greatest progress in mathematics and natural philosophy were to be awarded a prize from the fund. The prize was awarded every year from 1769 to 1998 except 1917. From 1769 to 1885, the prize was awarded for the best performance in a series of examinations. In 1854 Sir George Stokes, 1st Baronet, George Stokes included an examination question on a particular theorem that William Thomson, 1st Baron Kelvin, William Thomson had ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Senior Wrangler
The Senior Wrangler is the top mathematics undergraduate at the University of Cambridge in England, a position which has been described as "the greatest intellectual achievement attainable in Britain". Specifically, it is the person who achieves the highest overall mark among the Wranglers – the students at Cambridge who gain first-class degrees in mathematics. The Cambridge undergraduate mathematics course, or Mathematical Tripos, is famously difficult. Many Senior Wranglers have become world-leading figures in mathematics, physics, and other fields. They include George Airy, Jacob Bronowski, Christopher Budd, Kevin Buzzard, Arthur Cayley, Henry Cotterill, Donald Coxeter, Arthur Eddington, Ben Green, John Herschel, James Inman, J. E. Littlewood, Lee Hsien Loong, Jayant Narlikar, William Paley, Morris Pell, John Polkinghorne, Frank Ramsey, Lord Rayleigh (John Strutt), Sir George Stokes, Isaac Todhunter, Sir Gilbert Walker, and James H. Wilkinson. Senior Wr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Perse School
The Perse School is a Private schools in the United Kingdom, private school (English Private schools in the United Kingdom, fee-charging Day school, day and, in the case of the Perse, a former boarding school) in Cambridge, England. Founded in 1615 by Stephen Perse, its motto is ''Qui facit per alium facit per se'', taken to mean 'He who does things for others does them for himself'. The Perse School took girls for Sixth form only from 1994, began accepting girls at 11 and 13+ in September 2010 and was fully co-educational by September 2012. 'Perse' is a member of the Headmasters' and Headmistresses' Conference, an association of UK independent schools. The organisation now comprises three schools, which together provide for children aged 3 through to 18. The Pelican is the Perse's nursery and pre-preparatory school, and accommodates pupils from 3–7. It is situated on Glebe Road, close to the main school site. Preparatory education for students aged 7 to 11 years old is prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (to allow division), or equivalently, the concept of addition and subtraction. Combining these two ideas, one obtains a continuous group where multiplying points and their inverses is continuous. If the multiplication and taking of inverses are smoothness, smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the circle group. Rotating a circle is an example of a continuous symmetry. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soliton
In mathematics and physics, a soliton is a nonlinear, self-reinforcing, localized wave packet that is , in that it preserves its shape while propagating freely, at constant velocity, and recovers it even after collisions with other such localized wave packets. Its remarkable stability can be traced to a balanced cancellation of nonlinear and dispersive effects in the medium.Dispersive effects are a property of certain systems where the speed of a wave depends on its frequency. Solitons were subsequently found to provide stable solutions of a wide class of weakly nonlinear dispersive partial differential equations describing physical systems. The soliton phenomenon was first described in 1834 by John Scott Russell who observed a solitary wave in the Union Canal in Scotland. He reproduced the phenomenon in a wave tank and named it the " Wave of Translation". The Korteweg–de Vries equation was later formulated to model such waves, and the term "soliton" was coined by Zabu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects. The fundamental objects of study in algebraic geometry are algebraic variety, algebraic varieties, which are geometric manifestations of solution set, solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are line (geometry), lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscate of Bernoulli, lemniscates and Cassini ovals. These are plane algebraic curves. A point of the plane lies on an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of points of special interest like singular point of a curve, singular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians was Thales of Miletus (); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem. The number of known mathematicians grew when Pythagoras of Samos () established the Pythagorean school, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Society Of Edinburgh
The Royal Society of Edinburgh (RSE) is Scotland's national academy of science and letters. It is a registered charity that operates on a wholly independent and non-partisan basis and provides public benefit throughout Scotland. It was established in 1783. , there are around 1,800 Fellows. The Society covers a broader range of fields than the Royal Society of London, including literature and history. The Fellowship includes people from a wide range of disciplines: science and technology, arts, humanities, medicine, social science, business, and public service. History At the start of the 18th century, Edinburgh's intellectual climate fostered many clubs and societies (see Scottish Enlightenment). Though there were several that treated the arts, sciences and medicine, the most prestigious was the Society for the Improvement of Medical Knowledge, commonly referred to as the Medical Society of Edinburgh, co-founded by the mathematician Colin Maclaurin in 1731. Maclaurin was u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biographical Memoirs Of Fellows Of The Royal Society
The ''Biographical Memoirs of Fellows of the Royal Society'' is an academic journal on the history of science published annually by the Royal Society. It publishes obituaries of Fellows of the Royal Society. It was established in 1932 as ''Obituary Notices of Fellows of the Royal Society'' and obtained its current title in 1955, with volume numbering restarting at 1. Prior to 1932, obituaries were published in the '' Proceedings of the Royal Society''. The memoirs are a significant historical record and most include a full bibliography of works by the subjects. The memoirs are often written by a scientist of the next generation, often one of the subject's own former students, or a close colleague. In many cases the author is also a Fellow. Notable biographies published in this journal include Albert Einstein, Alan Turing, Bertrand Russell Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British philosopher, logician, mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Society
The Royal Society, formally The Royal Society of London for Improving Natural Knowledge, is a learned society and the United Kingdom's national academy of sciences. The society fulfils a number of roles: promoting science and its benefits, recognising excellence in science, supporting outstanding science, providing scientific advice for policy, education and public engagement and fostering international and global co-operation. Founded on 28 November 1660, it was granted a royal charter by Charles II of England, King Charles II and is the oldest continuously existing scientific academy in the world. The society is governed by its Council, which is chaired by the society's president, according to a set of statutes and standing orders. The members of Council and the president are elected from and by its Fellows, the basic members of the society, who are themselves elected by existing Fellows. , there are about 1,700 fellows, allowed to use the postnominal title FRS (Fellow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |