|
Greenhouse–Geisser Correction
The Greenhouse–Geisser correction \widehat is a statistical method of adjusting for lack of sphericity in a repeated measures ANOVA. The correction functions as both an estimate of epsilon (sphericity) and a correction for lack of sphericity. The correction was proposed by Samuel Greenhouse and Seymour Geisser in 1959. The Greenhouse–Geisser correction is an estimate of sphericity (\widehat). If sphericity is met, then \varepsilon = 1 . If sphericity is not met, then epsilon will be less than 1 (and the degrees of freedom will be overestimated and the F-value will be inflated). To correct for this inflation, multiply the Greenhouse–Geisser estimate of epsilon to the degrees of freedom used to calculate the F critical value. An alternative correction that is believed to be less conservative is the Huynh–Feldt correction (1976). As a general rule of thumb, the Greenhouse–Geisser correction is the preferred correction method when the epsilon estimate is below 0.75. Other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mauchly's Sphericity Test
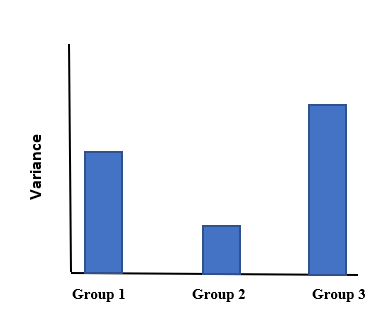
Mauchly's sphericity test or Mauchly's ''W'' is a statistical test used to validate a repeated measures analysis of variance (ANOVA). It was developed in 1940 by John Mauchly. Sphericity Sphericity is an important assumption of a repeated-measures ANOVA. It is the condition of equal variances among the differences between all possible pairs of within-subject conditions (i.e., levels of the independent variable). If sphericity is violated (i.e., if the variances of the differences between all combinations of the conditions are not equal), then the variance calculations may be distorted, which would result in an inflated F-ratio. Sphericity can be evaluated when there are three or more levels of a repeated measure factor and, with each additional repeated measures factor, the risk for violating sphericity increases. If sphericity is violated, a decision must be made as to whether a univariate or multivariate analysis is selected. If a univariate method is selected, the repeated-mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Repeated Measures ANOVA
A rerun or repeat is a rebroadcast of an episode of a radio or television program. The two types of reruns are those that occur during a hiatus and those that occur when a program is syndicated. Variations In the United Kingdom, the word "repeat" refers only to a single episode; "rerun" or "rerunning" is the preferred term for an entire series/season. A "repeat" is a single episode of a series that is broadcast outside its original timeslot on the same channel/network. The episode is usually the "repeat" of the scheduled episode that was broadcast in the original timeslot earlier the previous week. It allows viewers who were not able to watch the show in its timeslot to catch up before the next episode is broadcast. The term "rerun" can also be used in some respects as a synonym for "reprint", the equivalent term for print items; this is especially true for print items that are part of ongoing series such as comic strips. (''Peanuts'', for instance, has been in reruns since the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Samuel Greenhouse
Samuel W. Greenhouse (January 13, 1918 – September 29, 2000) was an American statistician who helped to pioneer the use of statistics in epidemiology. With Seymour Geisser, he developed the Greenhouse–Geisser correction, which is now widely used in the analysis of variance to correct for violations of the assumption of compound symmetry. Academic career Greenhouse was one of several founding statisticians at the National Institutes of Health (NIH), where, with Jerome Cornfield, Jacob Lieberman, Nathan Mantel, and Marvin Schneiderman, he co-founded the first biometry group in the National Cancer Institute in 1948. In 1954, Greenhouse became head of the theoretical statistics and applied mathematics section at the National Institute of Mental Health. He became chief of the National Institute of Child Health and Human Development's epidemiology and biometry branch in 1966, and continued to work there until 1974, when he joined the faculty of George Washington University (GWU) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seymour Geisser
Seymour Geisser (October 5, 1929 – March 11, 2004) was an American statistician noted for emphasizing predictive inference. In his book ''Predictive Inference: An Introduction'', he held that conventional statistical inference about unobservable population parameters amounts to inference about things that do not exist, following the work of Bruno de Finetti. He also pioneered the theory of cross-validation. With Samuel Greenhouse, he developed the Greenhouse–Geisser correction, which is now widely used in the analysis of variance to correct for violations of the assumption of compound symmetry. He testified as an expert on interpretation of DNA evidence in more than 100 civil and criminal trials. He held that prosecutors often relied on flawed statistical models. On that topic, he wrote "Statistics, Litigation and Conduct Unbecoming" in the book ''Statistical Science in the Courtroom'', edited by Joe oseph LouisGastwirth (Springer Verlag, 2000). Biography He was born in Ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Analysis Of Variance
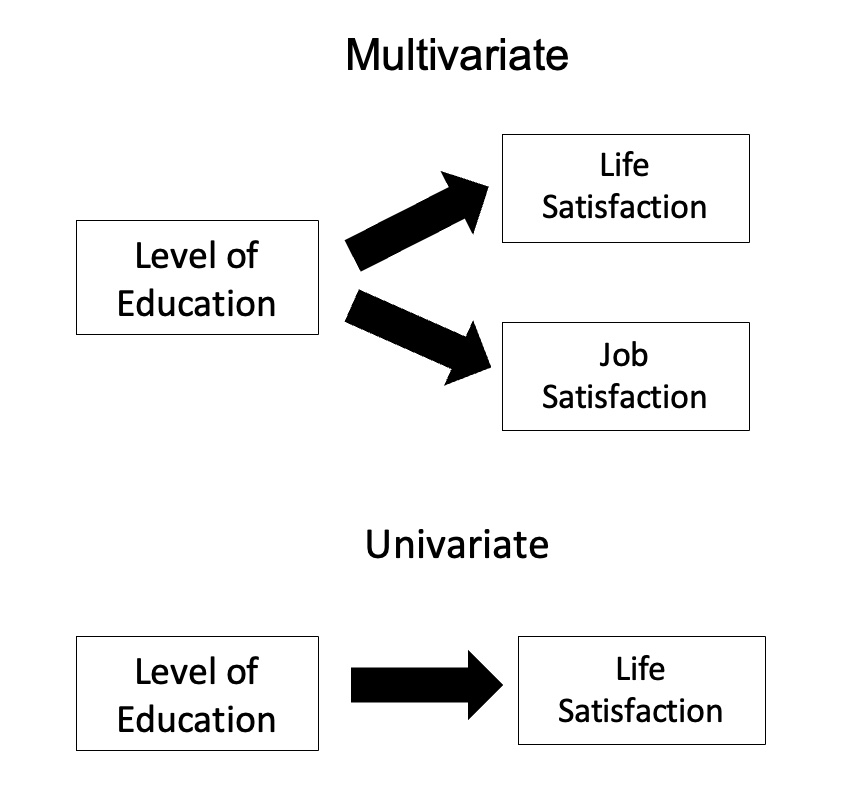
In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate random variable, multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests involving individual dependent variables separately. Without relation to the image, the dependent variables may be k life satisfactions scores measured at sequential time points and p job satisfaction scores measured at sequential time points. In this case there are k+p dependent variables whose linear combination follows a multivariate normal distribution, multivariate variance-covariance matrix homogeneity, and linear relationship, no multicollinearity, and each without outliers. Model Assume n q-dimensional observations, where the i’th observation y_i is assigned to the group g(i)\in \ and is distributed around the group center \mu^\in \mathbb R^q with Multivariate normal distribution, multivariate Ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |