|
Grashof Number
In fluid mechanics (especially fluid thermodynamics), the Grashof number (, after Franz Grashof) is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number (). Definition Heat transfer Free convection is caused by a change in density of a fluid due to a temperature change or gradient. Usually the density decreases due to an increase in temperature and causes the fluid to rise. This motion is caused by the buoyancy force. The major force that resists the motion is the viscous force. The Grashof number is a way to quantify the opposing forces. The Grashof number is: : \mathrm_L = \frac\, for vertical flat plates : \mathrm_D = \frac\, for pipes and bluff bodies where: * is gravitational acceleration due to Earth * is the coefficient of volume expansion (equal to approximately for ideal gases) * is the surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Mechanics
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasma (physics), plasmas) and the forces on them. Originally applied to water (hydromechanics), it found applications in a wide range of disciplines, including mechanical engineering, mechanical, aerospace engineering, aerospace, civil engineering, civil, chemical engineering, chemical, and biomedical engineering, as well as geophysics, oceanography, meteorology, astrophysics, and biology. It can be divided into ''fluid statics'', the study of various fluids at rest; and ''fluid dynamics'', the study of the effect of forces on fluid motion. It is a branch of ''continuum mechanics'', a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a macroscopic viewpoint rather than from microscopic. Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Transfer
Mass transfer is the net movement of mass from one location (usually meaning stream, phase, fraction, or component) to another. Mass transfer occurs in many processes, such as absorption, evaporation, drying, precipitation, membrane filtration, and distillation. Mass transfer is used by different scientific disciplines for different processes and mechanisms. The phrase is commonly used in engineering for physical processes that involve diffusive and convective transport of chemical species within physical systems. Some common examples of mass transfer processes are the evaporation of water from a pond to the atmosphere, the purification of blood in the kidneys and liver, and the distillation of alcohol. In industrial processes, mass transfer operations include separation of chemical components in distillation columns, absorbers such as scrubbers or stripping, adsorbers such as activated carbon beds, and liquid-liquid extraction. Mass transfer is often coupled to addit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Numbers Of Thermodynamics
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific units of volume used, such as in milliliters per milliliter (mL/mL). The number one is recognized as a dimensionless base quantity. Radians serve as dimensionless units for angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios in limits or derivatives often involve dimensionless quantities. In differential geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Numbers Of Fluid Mechanics
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into unit of measurement, units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined Unit of measurement, units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific Unit of volume, units of volume used, such as in milliliters per milliliter (mL/mL). The 1, number one is recognized as a dimensionless Base unit of measurement, base quantity. Radians serve as dimensionless units for Angle, angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyancy
Buoyancy (), or upthrust, is the force exerted by a fluid opposing the weight of a partially or fully immersed object (which may be also be a parcel of fluid). In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus, the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the Displacement (fluid), displaced fluid. For this reason, an object with average density greater than the surrounding fluid tends to sink because its weight is greater than the weight of the fluid it displaces. If the objec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buckingham π Theorem
In engineering, applied mathematics, and physics, the Buckingham theorem is a key theorem in dimensional analysis. It is a formalisation of Rayleigh's method of dimensional analysis. Loosely, the theorem states that if there is a physically meaningful equation involving a certain number ''n'' physical variables, then the original equation can be rewritten in terms of a set of ''p'' = ''n'' − ''k'' dimensionless parameters 1, 2, ..., ''p'' constructed from the original variables, where ''k'' is the number of physical dimensions involved; it is obtained as the rank of a particular matrix. The theorem provides a method for computing sets of dimensionless parameters from the given variables, or nondimensionalization, even if the form of the equation is still unknown. The Buckingham theorem indicates that validity of the laws of physics does not depend on a specific unit system. A statement of this theorem is that any physical law can be expressed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Volume
In thermodynamics, the specific volume of a substance (symbol: , nu) is the quotient of the substance's volume () to its mass (): :\nu = \frac It is a mass-specific intrinsic property of the substance. It is the reciprocal of density (rho) and it is also related to the molar volume and molar mass: :\nu = \rho^ = \frac The standard unit of specific volume is cubic meters per kilogram (m3/kg), but other units include ft3/lb, ft3/slug, or mL/g. Specific volume for an ideal gas is related to the molar gas constant () and the gas's temperature (), pressure (), and molar mass (): : \nu = \frac It's based on the ideal gas law, PV = , and the amount of substance In chemistry, the amount of substance (symbol ) in a given sample of matter is defined as a ratio () between the particle number, number of elementary entities () and the Avogadro constant (). The unit of amount of substance in the International ..., n = m/M Applications Specific volume is commonly applied to: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richardson Number
The Richardson number (Ri) is named after Lewis Fry Richardson (1881–1953). It is the dimensionless number that expresses the ratio of the buoyancy term to the flow velocity, flow shear (fluid), shear term: : \mathrm = \frac = \frac \frac where g is gravitational acceleration, gravity, \rho is density, u is a representative flow speed, and z is depth. The Richardson number, or one of several variants, is of practical importance in weather forecasting and in investigating density and turbidity currents in oceans, lakes, and reservoirs. When considering flows in which density differences are small (the Boussinesq approximation (buoyancy), Boussinesq approximation), it is common to use the Boussinesq approximation (buoyancy)#Advantages, reduced gravity ''g' '' and the relevant parameter is the densimetric Richardson number : \mathrm = \frac which is used frequently when considering atmospheric or oceanic flows. If the Richardson number is much less than unity, buoyancy is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combined Forced And Natural Convection
In fluid thermodynamics, combined forced convection and natural convection, or mixed convection, occurs when natural convection and forced convection mechanisms act together to transfer heat. This is also defined as situations where both pressure forces and buoyant forces interact. How much each form of convection contributes to the heat transfer is largely determined by the flow, temperature, geometry, and orientation. The nature of the fluid is also influential, since the Grashof number increases in a fluid as temperature increases, but is maximized at some point for a gas. Characterization Mixed convection problems are characterized by the Grashof number (for the natural convection) and the Reynolds number (for the forced convection). The relative effect of buoyancy on mixed convection can be expressed through the Richardson number: : \mathrm=\frac The respective length scales for each dimensionless number must be chosen depending on the problem, e.g. a vertical length for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
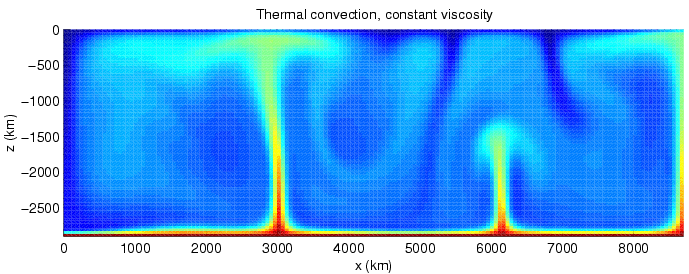
Rayleigh Number
In fluid mechanics, the Rayleigh number (, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108. The Rayleigh number is defined as the product of the Grashof number (), which describes the relationship between buoyancy and viscosity within a fluid, and the Prandtl number (), which describes the relationship between momentum diffusivity and thermal diffusivity: . Hence it may also be viewed as the ratio of buoyancy and viscosity forces multiplied by the ratio of momentum and thermal diffusivities: . It is closely related to the Nusselt number (). D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative density" or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |