|
Generalized Chi-squared Distribution
In probability theory and statistics, the generalized chi-squared distribution (or generalized chi-square distribution) is the distribution of a quadratic function of a multivariate normal distribution, multinormal variable (normal vector), or a linear combination of different normal variables and squares of normal variables. Equivalently, it is also a linear sum of independent noncentral chi-squared distribution, noncentral chi-square variables and a normal distribution, normal variable. There are several other such generalizations for which the same term is sometimes used; some of them are special cases of the family discussed here, for example the gamma distribution. Definition The generalized chi-squared variable may be described in multiple ways. One is to write it as a weighted sum of independent Noncentral chi-squared distribution, noncentral chi-square variables ^2 and a standard normal variable z: :\tilde(\boldsymbol, \boldsymbol, \boldsymbol,s,m)=\sum_i w_i ^2 (k_i,\la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Chi-square PDF
A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements (thus creating a conceptual model). As such, they are the essential basis of all valid deductive inferences (particularly in logic, mathematics and science), where the process of verification is necessary to determine whether a generalization holds true for any given situation. Generalization can also be used to refer to the process of identifying the parts of a whole, as belonging to the whole. The parts, which might be unrelated when left on their own, may be brought together as a group, hence belonging to the whole by establishing a common relation between them. However, the parts cannot be generalized into a whole—until a common relation is established among ''all'' parts. This does not mean that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
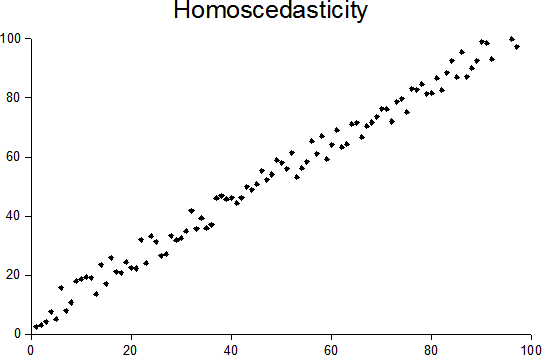
Heteroscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. “Skedasticity” comes from the Ancient Greek word “skedánnymi”, meaning “to scatter”. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Independence
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Normal Distribution
In probability theory, the family of complex normal distributions, denoted \mathcal or \mathcal_, characterizes complex random variables whose real and imaginary parts are jointly normal. The complex normal family has three parameters: ''location'' parameter ''μ'', ''covariance'' matrix \Gamma, and the ''relation'' matrix C. The standard complex normal is the univariate distribution with \mu = 0, \Gamma=1, and C=0. An important subclass of complex normal family is called the circularly-symmetric (central) complex normal and corresponds to the case of zero relation matrix and zero mean: \mu = 0 and C=0 . This case is used extensively in signal processing, where it is sometimes referred to as just complex normal in the literature. Definitions Complex standard normal random variable The standard complex normal random variable or standard complex Gaussian random variable is a complex random variable Z whose real and imaginary parts are independent normally distributed random v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wireless
Wireless communication (or just wireless, when the context allows) is the transfer of information (''telecommunication'') between two or more points without the use of an electrical conductor, optical fiber or other continuous guided transmission medium, medium for the transfer. The most common wireless technologies use radio waves. With radio waves, intended distances can be short, such as a few meters for Bluetooth, or as far as millions of kilometers for NASA Deep Space Network, deep-space radio communications. It encompasses various types of fixed, mobile, and portable applications, including two-way radios, Mobile phone, cellular telephones, personal digital assistants (PDAs), and wireless networking. Other examples of applications of radio ''wireless technology'' include Global Positioning System, GPS units, garage door openers, wireless Mouse (computing), computer mouse, Keyboard (computing), keyboards and Headset (audio), headsets, headphones, radio receivers, satelli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MIMO
In radio, multiple-input and multiple-output (MIMO) () is a method for multiplying the capacity of a radio link using multiple transmission and receiving antennas to exploit multipath propagation. MIMO has become an essential element of wireless communication standards including IEEE 802.11n (Wi-Fi 4), IEEE 802.11ac (Wi-Fi 5), HSPA+ (3G), WiMAX, and Long Term Evolution (LTE). More recently, MIMO has been applied to power-line communication for three-wire installations as part of the ITU G.hn standard and of the HomePlug AV2 specification. At one time, in wireless the term "MIMO" referred to the use of multiple antennas at the transmitter and the receiver. In modern usage, "MIMO" specifically refers to a class of techniques for sending and receiving more than one data signal simultaneously over the same radio channel by exploiting the difference in signal propagation between different antennas (e.g. due to multipath propagation). Additionally, modern MIMO usage often refer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renewal Theory
Renewal theory is the branch of probability theory that generalizes the Poisson process for arbitrary holding times. Instead of exponentially distributed holding times, a renewal process may have any independent and identically distributed (IID) holding times that have finite expectation. A renewal-reward process additionally has a random sequence of rewards incurred at each holding time, which are IID but need not be independent of the holding times. A renewal process has asymptotic properties analogous to the strong law of large numbers and central limit theorem. The renewal function m(t) (expected number of arrivals) and reward function g(t) (expected reward value) are of key importance in renewal theory. The renewal function satisfies a recursive integral equation, the renewal equation. The key renewal equation gives the limiting value of the convolution of m'(t) with a suitable non-negative function. The superposition of renewal processes can be studied as a special case of M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Classifier
In statistics, a quadratic classifier is a statistical classifier that uses a quadratic decision surface to separate measurements of two or more classes of objects or events. It is a more general version of the linear classifier. The classification problem Statistical classification considers a set of vectors of observations of an object or event, each of which has a known type . This set is referred to as the training set. The problem is then to determine, for a given new observation vector, what the best class should be. For a quadratic classifier, the correct solution is assumed to be quadratic in the measurements, so will be decided based on \mathbf + \mathbf + c In the special case where each observation consists of two measurements, this means that the surfaces separating the classes will be conic sections (i.e., either a line, a circle or ellipse, a parabola or a hyperbola). In this sense, we can state that a quadratic model is a generalization of the linear model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Form
In mathematics, a quadratic form is a polynomial with terms all of degree two (" form" is another name for a homogeneous polynomial). For example, 4x^2 + 2xy - 3y^2 is a quadratic form in the variables and . The coefficients usually belong to a fixed field , such as the real or complex numbers, and one speaks of a quadratic form ''over'' . Over the reals, a quadratic form is said to be '' definite'' if it takes the value zero only when all its variables are simultaneously zero; otherwise it is '' isotropic''. Quadratic forms occupy a central place in various branches of mathematics, including number theory, linear algebra, group theory ( orthogonal groups), differential geometry (the Riemannian metric, the second fundamental form), differential topology ( intersection forms of manifolds, especially four-manifolds), Lie theory (the Killing form), and statistics (where the exponent of a zero-mean multivariate normal distribution has the quadratic form -\mathbf^\math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |