|
GNOME Calculator
GNOME Calculator, formerly known as gcalctool, is the software calculator integrated with the GNOME, GNOME desktop environment. It is programmed in C (programming language), C and Vala (programming language), Vala and part of the GNOME Core Applications. Mathematics GNOME Calculator uses the MPFR library for extended precision arithmetic. It can support complex number arithmetic, perform factorization of integers, and define new functions by composition. Views While most functionality can be accessed by typing the function name into the input, Calculator provides different views for convenience. * ''Basic'' – interface for basic arithmetic, resembling a desk calculator. * ''Advanced'' – an interface with scientific functions, and support for custom variables. New functions can be defined by function composition. * ''Financial'' – financial calculation and currency converter, currency conversion. * ''Programming'' – a view with bitwise operators, bit manipulation operato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GNOME Core Applications
The GNOME Core Applications (also known as Apps for GNOME) are a software suite of software applications that are packaged as part of the standard free and open-source GNOME desktop environment. GNOME Core Applications have a consistent look and feel to the GNOME desktop, utilize the Adwaita (design language), Adwaita design language and tightly integrate with the GNOME desktop. GNOME Core Applications are developed and maintained through GNOME's official GitLab instance. A comprehensive list of these applications is available at Configuration * Settings – main interface to configure various aspects of GNOME. Diverse panels represent graphical front-ends to configure the NetworkManager, NetworkManager daemon and other daemons. Communication * Calls - initiating and answering Telephone call, phone calls and Voice over IP, VoIP calls (mainly utilized on Linux for mobile devices#Smartphones, Linux phones) * Contacts – the contacts book app Files * Document Scanner (S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
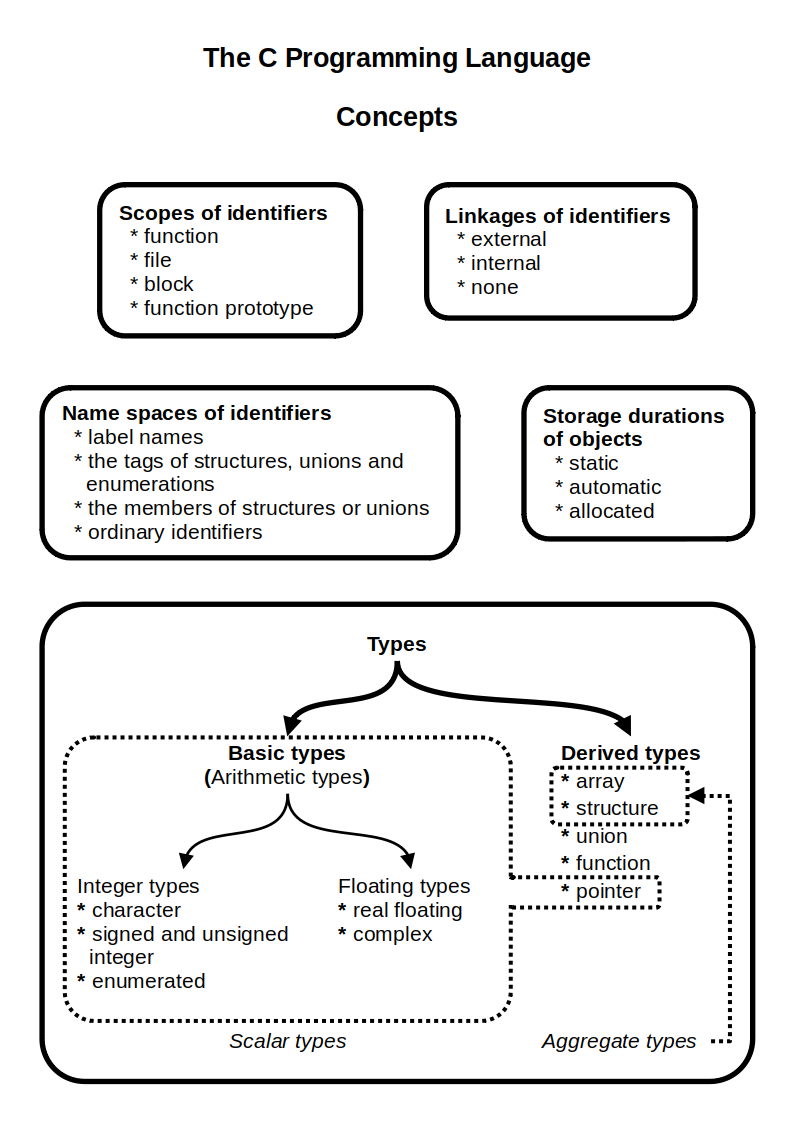
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Function
In mathematics, a binary function (also called bivariate function, or function of two variables) is a function that takes two inputs. Precisely stated, a function f is binary if there exists sets X, Y, Z such that :\,f \colon X \times Y \rightarrow Z where X \times Y is the Cartesian product of X and Y. Alternative definitions Set-theoretically, a binary function can be represented as a subset of the Cartesian product X \times Y \times Z, where (x,y,z) belongs to the subset if and only if f(x,y) = z. Conversely, a subset R defines a binary function if and only if for any x \in X and y \in Y, there exists a unique z \in Z such that (x,y,z) belongs to R. f(x,y) is then defined to be this z. Alternatively, a binary function may be interpreted as simply a function from X \times Y to Z. Even when thought of this way, however, one generally writes f(x,y) instead of f((x,y)). (That is, the same pair of parentheses is used to indicate both function application and the formation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Software That Uses Meson
Software consists of computer programs that instruct the execution of a computer. Software also includes design documents and specifications. The history of software is closely tied to the development of digital computers in the mid-20th century. Early programs were written in the machine language specific to the hardware. The introduction of high-level programming languages in 1958 allowed for more human-readable instructions, making software development easier and more portable across different computer architectures. Software in a programming language is run through a compiler or interpreter to execute on the architecture's hardware. Over time, software has become complex, owing to developments in networking, operating systems, and databases. Software can generally be categorized into two main types: # operating systems, which manage hardware resources and provide services for applications # application software, which performs specific tasks for users The rise of clou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
KCalc
KCalc is a scientific software calculator integrated with the KDE Gear. Functions KCalc includes trigonometric functions, logic operations, saved previous results, copy and paste, a configure UI, and statistical computations. The history function uses a stack method. KCalc also supports boolean operations. KCalc does not support graphing. Since version 2 (included in KDE 3.5) KCalc offers arbitrary precision. Gallery File:KCalc 21.12.0 science mode screenshot.png, Science mode File:KCalc 21.12.0 statistic mode screenshot.png, Statistic mode File:KCalc 21.12.0 numeral system mode screenshot.png, Numeral System mode See also * Comparison of software calculators * GNOME Calculator GNOME Calculator, formerly known as gcalctool, is the software calculator integrated with the GNOME, GNOME desktop environment. It is programmed in C (programming language), C and Vala (programming language), Vala and part of the GNOME Core Appli ... External links The KCalc Handbook Refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Of Software Calculators
This is a list of notable software calculators. Immediate execution calculators (button-oriented) , - Age Calculator (Gregorian & Hijri)ref> , Public domain , Web , Date-level (Gregorian & Hijri) , No , No , No Expression or formula calculators (command-line oriented) See also * Software calculator * Calculator input methods * Formula calculator * Calculator * Graphing calculator * Scientific calculator A scientific calculator is an Electronics, electronic calculator, either desktop or handheld, designed to perform calculations using basic (addition, subtraction, multiplication, Division (mathematics), division) and advanced (Trigonometric fun ... References {{DEFAULTSORT:Comparison Of Software Calculators Software calculators Comparisons of mathematical software ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numeric Keypad
A numeric keypad, number pad, numpad, or ten key, is the calculator-style group of ten numeric keys accompanied by other keys, usually on the far right side of computer keyboard. This grouping allows quick number entry with right hand, without the need to use both hands on number row of main keyboard. On a standard IBM PC keyboard, numpad has 17 keys, including digits to , (addition), (subtraction), (multiplication), and (Division (mathematics), division) symbols, (decimal point), , and keys. On smaller keyboards (such as those found on Laptop, laptops), the numeric keypad can be implemented as alternative markings on alphabetic keys (usually --, --, --) or added as a separate unit, that can be connected to a device by means such as USB; some of these may include keys not found on a standard numpad, such as a spacebar or a (or ) key. Sometimes it is necessary to distinguish between a key on the numpad and an equivalent key elsewhere on the keyboard. For example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unary Function
In mathematics, a unary function is a function that takes one argument. A unary operator belongs to a subset of unary functions, in that its codomain coincides with its domain. In contrast, a unary function's domain need not coincide with its range. Examples The successor function, denoted \operatorname, is a unary operator. Its domain and codomain are the natural numbers; its definition is as follows: : \begin \operatorname : \quad & \mathbb \rightarrow \mathbb \\ & n \mapsto (n + 1) \end In some programming languages such as C, executing this operation is denoted by postfixing to the operand, i.e. the use of is equivalent to executing the assignment n:= \operatorname(n). Many of the elementary functions are unary functions, including the trigonometric functions, logarithm with a specified base, exponentiation to a particular power or base, and hyperbolic functions. See also * Arity * Binary function * Binary operation * Iterated binary operation * Ternar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Postfix Notation
Reverse Polish notation (RPN), also known as reverse Łukasiewicz notation, Polish postfix notation or simply postfix notation, is a mathematical notation in which Operation (mathematics), operators ''follow'' their operands, in contrast to prefix notation, prefix or Polish notation (PN), in which operators ''precede'' their operands. The notation does not need any parentheses for as long as each operator has a fixed arity, number of operands. The term ''postfix notation'' describes the general scheme in mathematics and computer sciences, whereas the term ''reverse Polish notation'' typically refers specifically to the method used to enter calculations into hardware or software calculators, which often have additional side effect (computer science), side effects and implications depending on the actual implementation involving a stack (data structure), stack. The description "Polish" refers to the nationality of logician Jan Łukasiewicz, who invented Polish notation in 1924. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |