|
Formalism (linguistics)
In linguistics, the term formalism is used in a variety of meanings which relate to formal linguistics in different ways. In common usage, it is merely synonymous with a grammatical model or a syntactic model: a method for analyzing sentence structures. Such formalisms include different methodologies of generative grammar which are especially designed to produce grammatically correct strings of words; or the likes of Functional Discourse Grammar which builds on predicate logic. Additionally, ''formalism'' can be thought of as a theory of language. This is most commonly a reference to mathematical formalism which argues that syntax is purely axiomatic being based on sequences generated by mathematical operations. This idea stands in contradistinction to psychologism and logicism which, respectively, argue that syntax is based on human psychology; or on semantic a priori structures which exist independently of humans. Definitions Rudolph Carnap defined the meaning of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
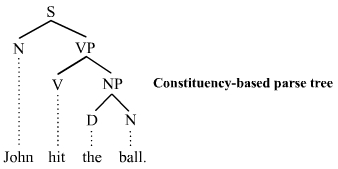
Parse Tree 1
Parsing, syntax analysis, or syntactic analysis is a process of analyzing a string of symbols, either in natural language, computer languages or data structures, conforming to the rules of a formal grammar by breaking it into parts. The term ''parsing'' comes from Latin ''pars'' (''orationis''), meaning part (of speech). The term has slightly different meanings in different branches of linguistics and computer science. Traditional sentence parsing is often performed as a method of understanding the exact meaning of a sentence or word, sometimes with the aid of devices such as sentence diagrams. It usually emphasizes the importance of grammatical divisions such as subject and predicate. Within computational linguistics the term is used to refer to the formal analysis by a computer of a sentence or other string of words into its constituents, resulting in a parse tree showing their syntactic relation to each other, which may also contain semantic information. Some parsing algori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Human Psychology
Psychology is the scientific study of mind and behavior. Its subject matter includes the behavior of humans and nonhumans, both conscious and unconscious phenomena, and mental processes such as thoughts, feelings, and motives. Psychology is an academic discipline of immense scope, crossing the boundaries between the natural and social sciences. Biological psychologists seek an understanding of the emergent properties of brains, linking the discipline to neuroscience. As social scientists, psychologists aim to understand the behavior of individuals and groups.Hockenbury & Hockenbury. Psychology. Worth Publishers, 2010. A professional practitioner or researcher involved in the discipline is called a psychologist. Some psychologists can also be classified as behavioral or cognitive scientists. Some psychologists attempt to understand the role of mental functions in individual and social behavior. Others explore the physiological and neurobiological processes that underli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formalism (philosophy Of Mathematics)
In the philosophy of mathematics, formalism is the view that holds that statements of mathematics and logic can be considered to be statements about the consequences of the manipulation of strings (alphanumeric sequences of symbols, usually as equations) using established manipulation rules. A central idea of formalism "is that mathematics is not a body of propositions representing an abstract sector of reality, but is much more akin to a game, bringing with it no more commitment to an ontology of objects or properties than ludo or chess." According to formalism, mathematical statements are not "about" numbers, sets, triangles, or any other mathematical objects in the way that physical statements are about material objects. Instead, they are purely syntactic expressions—formal strings of symbols manipulated according to explicit rules without inherent meaning. These symbolic expressions only acquire interpretation (or semantics) when we choose to assign it, similar to how che ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ferdinand De Saussure
Ferdinand Mongin de Saussure (; ; 26 November 185722 February 1913) was a Swiss linguist, semiotician and philosopher. His ideas laid a foundation for many significant developments in both linguistics and semiotics in the 20th century. He is widely considered one of the founders of 20th-century linguistics and one of two major founders (together with Charles Sanders Peirce) of semiotics, or ''semiology'', as Saussure called it. One of his translators, Roy Harris, summarized Saussure's contribution to linguistics and the study of "the whole range of human sciences. It is particularly marked in linguistics, philosophy, psychoanalysis, psychology, sociology and anthropology." Although they have undergone extension and critique over time, the dimensions of organization introduced by Saussure continue to inform contemporary approaches to the phenomenon of language. As Leonard Bloomfield stated after reviewing Saussure's work: "he has given us the theoretical basis for a science of h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Course In General Linguistics
''Course in General Linguistics'' () is a book compiled by Charles Bally and Albert Sechehaye from notes on lectures given by historical-comparative linguist Ferdinand de Saussure at the University of Geneva between 1906 and 1911. It was published in 1916, after Saussure's death, and is generally regarded as the starting point of structural linguistics, an approach to linguistics that was established in the first half of the 20th century by the Prague linguistic circle. One of Saussure's translators, Roy Harris, summarized Saussure's contribution to linguistics and the study of language in the following way: Although Saussure's perspective was in historical linguistics, the ''Course'' develops a theory of semiotics that is generally applicable. A manuscript containing Saussure's original notes was found in 1996, and later published as ''Writings in General Linguistics''. The task of linguistics Following a brief introduction to the history of linguistics, Saussure sets the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thought
In their most common sense, the terms thought and thinking refer to cognitive processes that can happen independently of sensory stimulation. Their most paradigmatic forms are judging, reasoning, concept formation, problem solving, and deliberation. But other mental processes, like considering an idea, memory, or imagination, are also often included. These processes can happen internally independent of the sensory organs, unlike perception. But when understood in the widest sense, any mental event may be understood as a form of thinking, including perception and unconscious mental processes. In a slightly different sense, the term ''thought'' refers not to the mental processes themselves but to mental states or systems of ideas brought about by these processes. Various theories of thinking have been proposed, some of which aim to capture the characteristic features of thought. '' Platonists'' hold that thinking consists in discerning and inspecting Platonic forms and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Proposition
A proposition is a statement that can be either true or false. It is a central concept in the philosophy of language, semantics, logic, and related fields. Propositions are the object s denoted by declarative sentences; for example, "The sky is blue" expresses the proposition that the sky is blue. Unlike sentences, propositions are not linguistic expressions, so the English sentence "Snow is white" and the German "Schnee ist weiß" denote the same proposition. Propositions also serve as the objects of belief and other propositional attitudes, such as when someone believes that the sky is blue. Formally, propositions are often modeled as functions which map a possible world to a truth value. For instance, the proposition that the sky is blue can be modeled as a function which would return the truth value T if given the actual world as input, but would return F if given some alternate world where the sky is green. However, a number of alternative formalizations have been pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Logic
Mathematical logic is the study of Logic#Formal logic, formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory (also known as computability theory). Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics. Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and Mathematical analysis, analysis. In the early 20th century it was shaped by David Hilbert's Hilbert's program, program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that represents removal of objects from a collection. For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches. Therefore, the ''difference'' of 5 and 2 is 3; that is, . While primarily associated with natural numbers in arithmetic, subtraction can also represent removing or decreasing physical and abstract quantities using different kinds of objects including negative numbers, Fraction (mathematics), fractions, irrational numbers, Euclidean vector, vectors, decimals, functions, and matrices. In a sense, subtraction is the inverse of addition. That is, if and only if . In words: the difference of two numbers is the number that gives the first one when added to the second one. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), division. The addition of two Natural number, whole numbers results in the total or ''summation, sum'' of those values combined. For example, the adjacent image shows two columns of apples, one with three apples and the other with two apples, totaling to five apples. This observation is expressed as , which is read as "three plus two Equality (mathematics), equals five". Besides counting items, addition can also be defined and executed without referring to concrete objects, using abstractions called numbers instead, such as integers, real numbers, and complex numbers. Addition belongs to arithmetic, a branch of mathematics. In algebra, another area of mathematics, addition can also be performed on abstract objects such as Euclidean vector, vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Number
In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter \aleph (aleph) marked with subscript indicating their rank among the infinite cardinals. Cardinality is defined in terms of bijective functions. Two sets have the same cardinality if, and only if, there is a one-to-one correspondence (bijection) between the elements of the two sets. In the case of finite sets, this agrees with the intuitive notion of number of elements. In the case of infinite sets, the behavior is more complex. A fundamental theorem due to Georg Cantor shows that it is possible for two infinite sets to have different cardinalities, and in particular the cardinality of the set of real numbers is gre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edmund Husserl
Edmund Gustav Albrecht Husserl (; 8 April 1859 – 27 April 1938) was an Austrian-German philosopher and mathematician who established the school of Phenomenology (philosophy), phenomenology. In his early work, he elaborated critiques of historicism and of psychologism in logic based on analyses of intentionality. In his mature work, he sought to develop a systematic foundational science based on the so-called Bracketing (phenomenology), phenomenological reduction. Arguing that Transcendence (philosophy), transcendental consciousness sets the limits of all possible knowledge, Husserl redefined phenomenology as a Transcendental idealism, transcendental-idealist philosophy. Husserl's thought profoundly influenced 20th-century philosophy, and he remains a notable figure in contemporary philosophy and beyond. Husserl studied mathematics, taught by Karl Weierstrass and Leo Königsberger, and philosophy taught by Franz Brentano and Carl Stumpf. He taught philosophy as a ''Privatdozent' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |