|
Exact Test
An exact (significance) test is a statistical test such that if the null hypothesis is true, then all assumptions made during the derivation of the distribution of the test statistic are met. Using an exact test provides a significance test that maintains the type I error rate of the test (\alpha) at the desired significance level of the test. For example, an exact test at a significance level of \alpha = 5\%, when repeated over many samples where the null hypothesis is true, will reject at most 5\% of the time. This is in contrast to an ''approximate test'' in which the desired type I error rate is only approximately maintained (i.e.: the test might reject > 5% of the time), while this approximation may be made as close to \alpha as desired by making the sample size sufficiently large. Exact tests that are based on discrete test statistics may be conservative, indicating that the actual rejection rate lies below the nominal significance level \alpha. As an example, this is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
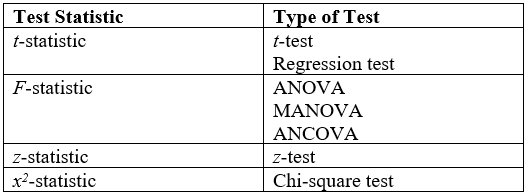 |
Statistical Test
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Permutation Test
A permutation test (also called re-randomization test or shuffle test) is an exact statistical hypothesis test. A permutation test involves two or more samples. The (possibly counterfactual) null hypothesis is that all samples come from the same distribution H_0: F=G. Under the null hypothesis, the distribution of the test statistic is obtained by calculating all possible values of the test statistic under possible rearrangements of the observed data. Permutation tests are, therefore, a form of resampling. Permutation tests can be understood as surrogate data testing where the surrogate data under the null hypothesis are obtained through permutations of the original data. In other words, the method by which treatments are allocated to subjects in an experimental design is mirrored in the analysis of that design. If the labels are exchangeable under the null hypothesis, then the resulting tests yield exact significance levels; see also exchangeability. Confidence intervals can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Statistical Methods For Research Workers
''Statistical Methods for Research Workers'' is a classic book on statistics, written by the statistician R. A. Fisher. It is considered by some to be one of the 20th century's most influential books on statistical methods, together with his '' The Design of Experiments'' (1935). It was originally published in 1925, by Oliver & Boyd (Edinburgh); the final and posthumous 14th edition was published in 1970. The impulse to write a book on the statistical methodology he had developed came not from Fisher himself but from D. Ward Cutler, one of the two editors of a series of "Biological Monographs and Manuals" being published by Oliver and Boyd. Reviews According to Denis Conniffe: Ronald A. Fisher was "interested in application and in the popularization of statistical methods and his early book ''Statistical Methods for Research Workers'', published in 1925, went through many editions and motivated and influenced the practical use of statistics in many fields of study. His ''Design ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Optimal Discriminant Analysis
Optimal Discriminant Analysis (ODA)Provider: John Wiley & Sons, Ltd Content:text/plain; charset="UTF-8" TY - JOUR AU - Yarnold, Paul R. AU - Soltysik, Robert C. TI - Theoretical Distributions of Optima for Univariate Discrimination of Random Data* JO - Decision Sciences VL - 22 IS - 4 PB - Blackwell Publishing Ltd SN - 1540-5915 UR - https://dx.doi.org/10.1111/j.1540-5915.1991.tb00362.x DO - 10.1111/j.1540-5915.1991.tb00362.x SP - 739 EP - 752 KW - Discrete Programming KW - Linear Statistical Models KW - Mathematical Programming KW - and Statistical Techniques PY - 1991 ER -1.tb00362.x and the related classification tree analysis (CTA) are exact statistical methods that maximize predictive accuracy. For any specific sample and exploratory or confirmatory hypothesis, optimal discriminant analysis (ODA) identifies the statistical model that yields maximum predictive accuracy, assesses the exact Type I error rate, and evaluates potential cross-generalizability. Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Exact Statistics
Exact statistics, such as that described in exact test, is a branch of statistics that was developed to provide more accurate results pertaining to statistical testing and interval estimation by eliminating procedures based on asymptotic and approximate statistical methods. The main characteristic of exact methods is that statistical tests and confidence intervals are based on exact probability statements that are valid for any sample size. Exact statistical methods help avoid some of the unreasonable assumptions of traditional statistical methods, such as the assumption of equal variances in classical ANOVA. They also allow exact inference on variance components of mixed models. When exact ''p''-values and confidence intervals are computed under a certain distribution, such as the normal distribution, then the underlying methods are referred to as exact parametric methods. The exact methods that do not make any distributional assumptions are referred to as exact nonparametric m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, Fisher was the one to most comprehensively combine the ideas of Gregor Mendel and Charles Darwin, as his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the Modern synthesis (20th century), modern synthesis. For his contributions to biology, Richard Dawkins declared Fisher to be the greatest of Darwin's successors. He is also considered one of the founding fathers of Neo-Darwinism. According to statistician Jeffrey T. Leek, Fisher is the most in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Likelihood-ratio Test
In statistics, the likelihood-ratio test is a hypothesis test that involves comparing the goodness of fit of two competing statistical models, typically one found by maximization over the entire parameter space and another found after imposing some constraint, based on the ratio of their likelihoods. If the more constrained model (i.e., the null hypothesis) is supported by the observed data, the two likelihoods should not differ by more than sampling error. Thus the likelihood-ratio test tests whether this ratio is significantly different from one, or equivalently whether its natural logarithm is significantly different from zero. The likelihood-ratio test, also known as Wilks test, is the oldest of the three classical approaches to hypothesis testing, together with the Lagrange multiplier test and the Wald test. In fact, the latter two can be conceptualized as approximations to the likelihood-ratio test, and are asymptotically equivalent. In the case of comparing two mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Pearson's Chi-squared Test
Pearson's chi-squared test or Pearson's \chi^2 test is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to ''Pearson χ-squared'' test or statistic are used. It is a p-value test. The setup is as follows: * Before the experiment, the experimenter fixes a certain number N of samples to take. * The observed data is (O_1, O_2, ..., O_n), the count number of samples from a finite set of given categories. They satisfy \sum_i O_i = N. * The null hypothesis is that the count numbers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
P-value
In null-hypothesis significance testing, the ''p''-value is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. A very small ''p''-value means that such an extreme observed outcome would be very unlikely ''under the null hypothesis''. Even though reporting ''p''-values of statistical tests is common practice in academic publications of many quantitative fields, misinterpretation and misuse of p-values is widespread and has been a major topic in mathematics and metascience. In 2016, the American Statistical Association (ASA) made a formal statement that "''p''-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone" and that "a ''p''-value, or statistical significance, does not measure the size of an effect or the importance of a result" or "evidence regarding a model or hypothesis". That ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |