|
Eugenia Cheng
Eugenia Loh-Gene Cheng is a British mathematician, educator and concert pianist. Her mathematical interests include higher category theory, and as a pianist she specialises in lieder and art song. She is also known for explaining mathematics to non-mathematicians to combat math phobia, often using analogies with food and baking. Cheng is a scientist-in-residence at the School of the Art Institute of Chicago. Early life and education Cheng was born in Hampshire, England. She moved to Sussex at the age of one. Her family is originally from Hong Kong. Her interest in mathematics stemmed from a young age thanks largely to her mother who made mathematics a part of life. Cheng attended Roedean School. She studied the Mathematical Tripos at the University of Cambridge, where she was a student of Gonville and Caius College, Cambridge. Her postgraduate research was supervised by Martin Hyland. Career and research As of 2020, Cheng is a scientist-in-residence at the School of the Ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phi Beta Kappa
The Phi Beta Kappa Society () is the oldest academic honor society in the United States. It was founded in 1776 at the College of William & Mary in Virginia. Phi Beta Kappa aims to promote and advocate excellence in the liberal arts and sciences, and to induct outstanding students of arts and sciences at select American colleges and universities. Since its inception, its inducted members include 17 President of the United States, United States presidents, 42 Supreme Court of the United States, United States Supreme Court justices, and 136 Nobel Prize, Nobel laureates. History Origins The Phi Beta Kappa Society had its first meeting on December 5, 1776, at the College of William & Mary in Williamsburg, Virginia by five students, with John Heath as its first President. The society established the precedent for naming American college societies after the initial letters of a secret Greek motto. The group consisted of students who frequented the Raleigh Tavern as a common meeting ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sussex
Sussex (Help:IPA/English, /ˈsʌsɪks/; from the Old English ''Sūþseaxe''; lit. 'South Saxons'; 'Sussex') is an area within South East England that was historically a kingdom of Sussex, kingdom and, later, a Historic counties of England, county. It includes the Ceremonial counties of England, ceremonial counties of East Sussex and West Sussex. The area borders the English Channel to the south, and the Ceremonial counties of England, ceremonial counties of Surrey to the north, Kent to the north-east, and Hampshire to the west. Sussex contains the city of Brighton and Hove and its wider Greater Brighton City Region, city region, as well as the South Downs National Park and the National Landscapes of the High Weald National Landscape, High Weald and Chichester Harbour. Its coastline is long. The Kingdom of Sussex emerged in the fifth century in the area that had previously been inhabited by the Regni tribe in the Roman Britain, Romano-British period. In about 827, shortly a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Same-sex Marriage
Same-sex marriage, also known as gay marriage, is the marriage of two people of the same legal Legal sex and gender, sex. marriage between same-sex couples is legally performed and recognized in 38 countries, with a total population of 1.5 billion people (20% of the world's population). The most recent jurisdiction to legalize same-sex marriage is Recognition of same-sex unions in Thailand, Thailand. Same-sex marriage is legally recognized in a large majority of the world's developed country, developed countries; notable exceptions are Recognition of same-sex unions in Italy, Italy, Recognition of same-sex unions in Japan, Japan, Recognition of same-sex unions in South Korea, South Korea and the Recognition of same-sex unions in the Czech Republic, Czech Republic. Same-sex adoption, Adoption rights are not necessarily covered, though most states with same-sex marriage allow those couples to jointly adopt as other married couples can. Some countries, such as Nigeria and Russ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Society Prizes For Science Books
The Royal Society Science Book Prize is an annual £25,000 prize awarded by the Royal Society to celebrate outstanding popular science books from around the world. It is open to authors of science books written for a non-specialist audience, and since it was established in 1988 has championed writers such as Stephen Hawking, Jared Diamond, Stephen Jay Gould and Bill Bryson. In 2015 ''The Guardian'' described the prize as "the most prestigious science book prize in Britain". History The Royal Society established the Science Books Prize in 1988 with the aim of encouraging the writing, publishing and reading of good and accessible popular science books. Its name has varied according to sponsorship agreements. Judging process A panel of judges decides the shortlist and the winner of the Prize each year. The panel is chaired by a fellow of the Royal Society and includes authors, scientists and media personalities. The judges for the 2016 prize included author Bill Bryson, theoretic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
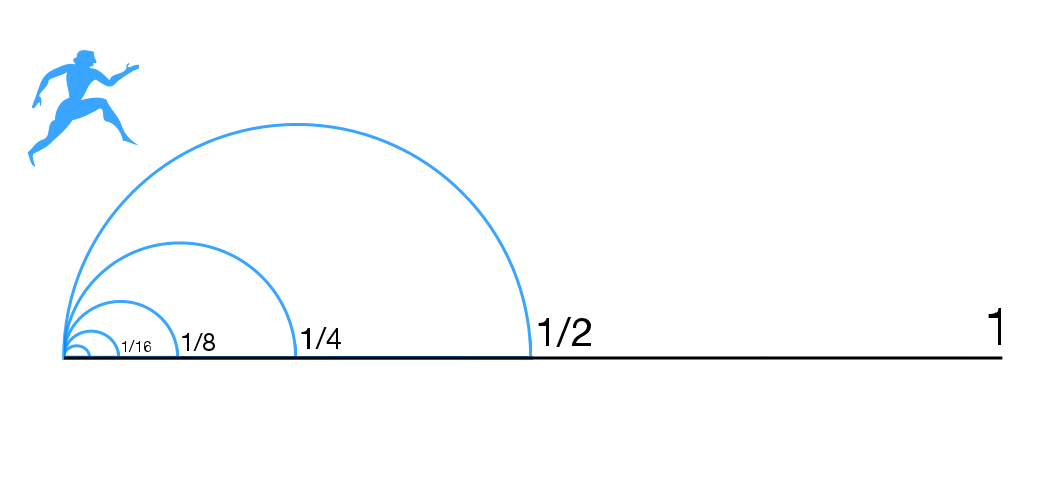
Zeno's Paradoxes
Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through the works of Plato, Aristotle, and later commentators like Simplicius of Cilicia. Zeno devised these paradoxes to support his teacher Parmenides's philosophy of monism, which posits that despite people's sensory experiences, reality is singular and unchanging. The paradoxes famously challenge the notions of plurality (the existence of many things), motion, space, and time by suggesting they lead to logical contradictions. Zeno's work, primarily known from second-hand accounts since his original texts are lost, comprises forty "paradoxes of plurality," which argue against the coherence of believing in multiple existences, and several arguments against motion and change. Of these, only a few are definitively known today, including the renowned "Achilles Paradox", which illustrates the problematic concept of infinite divisibi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cantor's Diagonal Argument
Cantor's diagonal argument (among various similar namesthe diagonalisation argument, the diagonal slash argument, the anti-diagonal argument, the diagonal method, and Cantor's diagonalization proof) is a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbersinformally, that there are sets which in some sense contain more elements than there are positive integers. Such sets are now called uncountable sets, and the size of infinite sets is treated by the theory of cardinal numbers, which Cantor began. Georg Cantor published this proof in 1891, English translation: but it was not his first proof of the uncountability of the real numbers, which appeared in 1874. However, it demonstrates a general technique that has since been used in a wide range of proofs, including the first of Gödel's incompleteness theorems and Turing's answer to the ''Entscheidungsproblem''. Diagonalization arguments ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Theory
Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathematics – is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of ''naive set theory''. After the discovery of Paradoxes of set theory, paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beyond Infinity (mathematics Book)
Beyond Infinity may refer to: *"Beyond Infinity", science fiction radio play by Villiers Gerson, aired in 1950 as an episode of ''Dimension X'' * ''Beyond Infinity'' (short story collection), a collection of science fiction stories by Robert Spencer Carr, published in 1951 *'' Beyond Infinity'', alternative title of 1961 science fiction anthology by Alan E. Nourse *Beyond Infinity, the distribution company for the 1987 science fiction comedy film ''Galactic Gigolo'' *'' Beyond Infinity'', science fiction novel by Gregory Benford *'' Beyond Infinity'', anime adaption of manga series ''Babel II'' *"Beyond Infinity", track on 2008 synth concept album '' Reality After Midnight'' by William C. Woxlin *" Beyond Infinity", 2011 Brazilian death metal track by Thyresis * ''Beyond Infinity'' (mathematics book), nonfiction book about infinity by Eugenia Cheng, published in 2017 See also *''Au-delà de l'Infini'' 'Beyond Infinity'' 1952 French science fiction novel by Henri René Guieu *''Slav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The New York Times
''The New York Times'' (''NYT'') is an American daily newspaper based in New York City. ''The New York Times'' covers domestic, national, and international news, and publishes opinion pieces, investigative reports, and reviews. As one of the longest-running newspapers in the United States, the ''Times'' serves as one of the country's Newspaper of record, newspapers of record. , ''The New York Times'' had 9.13 million total and 8.83 million online subscribers, both by significant margins the List of newspapers in the United States, highest numbers for any newspaper in the United States; the total also included 296,330 print subscribers, making the ''Times'' the second-largest newspaper by print circulation in the United States, following ''The Wall Street Journal'', also based in New York City. ''The New York Times'' is published by the New York Times Company; since 1896, the company has been chaired by the Ochs-Sulzberger family, whose current chairman and the paper's publ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kirkus Reviews
''Kirkus Reviews'' is an American book review magazine founded in 1933 by Virginia Kirkus. The magazine's publisher, Kirkus Media, is headquartered in New York City. ''Kirkus Reviews'' confers the annual Kirkus Prize to authors of fiction, nonfiction, and young readers' literature. ''Kirkus Reviews'', published on the first and 15th of each month, previews books before their publication. ''Kirkus'' reviews over 10,000 titles per year. History Virginia Kirkus was hired by Harper & Brothers to establish a children's book department in 1926. In 1932, the department was eliminated as an economic measure. However, within a year, Louise Raymond, the secretary Kirkus hired, had the department running again. Kirkus, however, had left and soon established her own book review service. Initially, she arranged to get galley proofs of "20 or so" books in advance of their publication; almost 80 years later, the service was receiving hundreds of books weekly and reviewing about 100. Ini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in most areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient space (other), quotient spaces, direct products, completion, and duality (mathematics), duality. Many areas of computer science also rely on category theory, such as functional programming and Semantics (computer science), semantics. A category (mathematics), category is formed by two sorts of mathematical object, objects: the object (category theory), objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. Metapho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Notes In Theoretical Computer Science
''Electronic Notes in Theoretical Computer Science'' is an electronic computer science journal published by Elsevier, started in 1995. Its issues include many post-proceedings for workshops, etc. The journal is abstracted and indexed in Scopus and Science Citation Index The Science Citation Index Expanded (SCIE) is a citation index owned by Clarivate and previously by Thomson Reuters. It was created by the Eugene Garfield at the Institute for Scientific Information, launched in 1964 as Science Citation Index ( .... Electronic Notes in Theoretical Computer Science has been discontinued as of 2021. References Computer science journals Elsevier academic journals Academic journals established in 1995 {{comp-sci-theory-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |