|
Ellipsoidal Latitude
The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an '' oblate ellipsoid'', a slightly flattened sphere. A ''geodesic'' is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry . If the Earth is treated as a sphere, the geodesics are great circles (all of which are closed) and the problems reduce to ones in spherical trigonometry. However, showed that the effect of the rotation of the Earth results in its resembling a slightly oblate ellipsoid: in this case, the equator and the meridians are the only simple closed geodesics. Furthermore, the shortest path between two points on the equator does not necessarily run along the equator. Finally, if the ellipsoid is further perturbed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long Geodesic On An Oblate Ellipsoid
Long may refer to: Measurement * Long, characteristic of something of great duration * Long, characteristic of something of great length * Longitude (abbreviation: long.), a geographic coordinate * Longa (music), note value in early music mensural notation Places Asia * Long District, Laos * Long District, Phrae, Thailand * Longjiang (other) or River Long (lit. "dragon river"), one of several rivers in China * Yangtze River or Changjiang (lit. "Long River"), China Elsewhere * Long, Somme, France People * Long (Chinese surname) * Long (Western surname) Fictional characters * Long (''Bloody Roar''), in the video game series * Long, Aeon of Permanence in Honkai: Star Rail Sports * Long, a fielding term in cricket * Long, in tennis and similar games, beyond the service line during a serve and beyond the baseline during play Other uses * , a U.S. Navy ship name * Long (finance), a position in finance, especially stock markets * Lòng, name for a laneway in S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic Problem On An Ellipsoid
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun ''geodesic'' and the adjective '' geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clairaut's Relation
In classical differential geometry, Clairaut's relation, named after Alexis Claude de Clairaut, is a formula that characterizes the great circle paths on the unit sphere. The formula states that if γ is a parametrization of a great circle then : \rho(\gamma(t)) \sin \psi(\gamma(t)) = \text,\, where ''ρ''(''P'') is the distance from a point ''P'' on the great circle to the ''z''-axis, and ''ψ''(''P'') is the angle between the great circle and the meridian through the point ''P''. The relation remains valid for a geodesic on an arbitrary surface of revolution. A statement of the general version of Clairaut's relation is: Pressley (p. 185) explains this theorem as an expression of conservation of angular momentum Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ... abou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beltrami Identity
The Beltrami identity, named after Eugenio Beltrami, is a special case of the Euler–Lagrange equation in the calculus of variations. The Euler–Lagrange equation serves to extremize action functionals of the form :I \int_a^b L ,u(x),u'(x)\, dx \, , where a and b are constants and u'(x) = \frac. If \frac = 0, then the Euler–Lagrange equation reduces to the Beltrami identity, where is a constant.Weisstein, Eric W"Euler-Lagrange Differential Equation." FroMathWorld-A Wolfram Web Resource. See Eq. (5).Thus, the Legendre transform of the Lagrangian, the Hamiltonian, is constant along the dynamical path. Derivation By the chain rule, the derivative of is : \frac = \frac \frac + \frac \frac + \frac \frac \, . Because \frac = 0 , we write : \frac = \frac u' + \frac u'' \, . We have an expression for \frac from the Euler–Lagrange equation, : \frac = \frac \frac \, that we can substitute in the above expression for \frac to obtain : \frac =u'\frac \frac + u''\frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or variational calculus) is a field of mathematical analysis that uses variations, which are small changes in Function (mathematics), functions and functional (mathematics), functionals, to find maxima and minima of functionals: Map (mathematics), mappings from a set of Function (mathematics), functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, ''Mécanique analytique''. Lagrangian mechanics describes a mechanical system as a pair consisting of a configuration space (physics), configuration space ''M'' and a smooth function L within that space called a ''Lagrangian''. For many systems, , where ''T'' and ''V'' are the Kinetic energy, kinetic and Potential energy, potential energy of the system, respectively. The stationary action principle requires that the Action (physics)#Action (functional), action functional of the system derived from ''L'' must remain at a stationary point (specifically, a Maximum and minimum, maximum, Maximum and minimum, minimum, or Saddle point, saddle point) throughout the time evoluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth Radius
Earth radius (denoted as ''R''🜨 or ''R''E) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid (an oblate ellipsoid), the radius ranges from a maximum (equatorial radius, denoted ''a'') of about to a minimum (polar radius, denoted ''b'') of nearly . A globally-average value is usually considered to be with a 0.3% variability (±10 km) for the following reasons. The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the ''mean radius'' (''R'') of three radii measured at two equator points and a pole; the ''authalic radius'', which is the radius of a sphere with the same surface area (''R''); and the ''volumetric radius'', which is the radius of a sphere having the same volume as the ellipsoid (''R''). All three values are about . Other ways to define and measure the Earth's radius involve either the spheroid's radius of curvature or the actual topography. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (mathematics)
In mathematics, the eccentricity of a Conic section#Eccentricity, conic section is a non-negative real number that uniquely characterizes its shape. One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular: * The eccentricity of a circle is 0. * The eccentricity of a non-circular ellipse is between 0 and 1. * The eccentricity of a parabola is 1. * The eccentricity of a hyperbola is greater than 1. * The eccentricity of a pair of Line (geometry), lines is \infty. Two conic sections with the same eccentricity are similarity (geometry), similar. Definitions Any conic section can be defined as the Locus (mathematics), locus of points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. That ratio is called the ''eccentricity'', commonly denoted as . The eccentricity can also be defined in terms of the intersection of a plane and a Cone (geometry), double-napped cone associated with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great-circle Navigation
Great-circle navigation or orthodromic navigation (related to orthodromic course; ) is the practice of navigating a vessel (a ship or aircraft) along a great circle. Such routes yield the shortest distance between two points on the globe. Course The great circle path may be found using spherical trigonometry; this is the spherical version of the ''inverse geodetic problem''. If a navigator begins at ''P''1 = (φ1,λ1) and plans to travel the great circle to a point at point ''P''2 = (φ2,λ2) (see Fig. 1, φ is the latitude, positive northward, and λ is the longitude, positive eastward), the initial and final courses α1 and α2 are given by formulas for solving a spherical triangle :\begin \tan\alpha_1&=\frac,\\ \tan\alpha_2&=\frac,\\ \end where λ12 = λ2 − λ1In the article on great-circle distances, the notation Δλ = λ12 and Δσ&n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
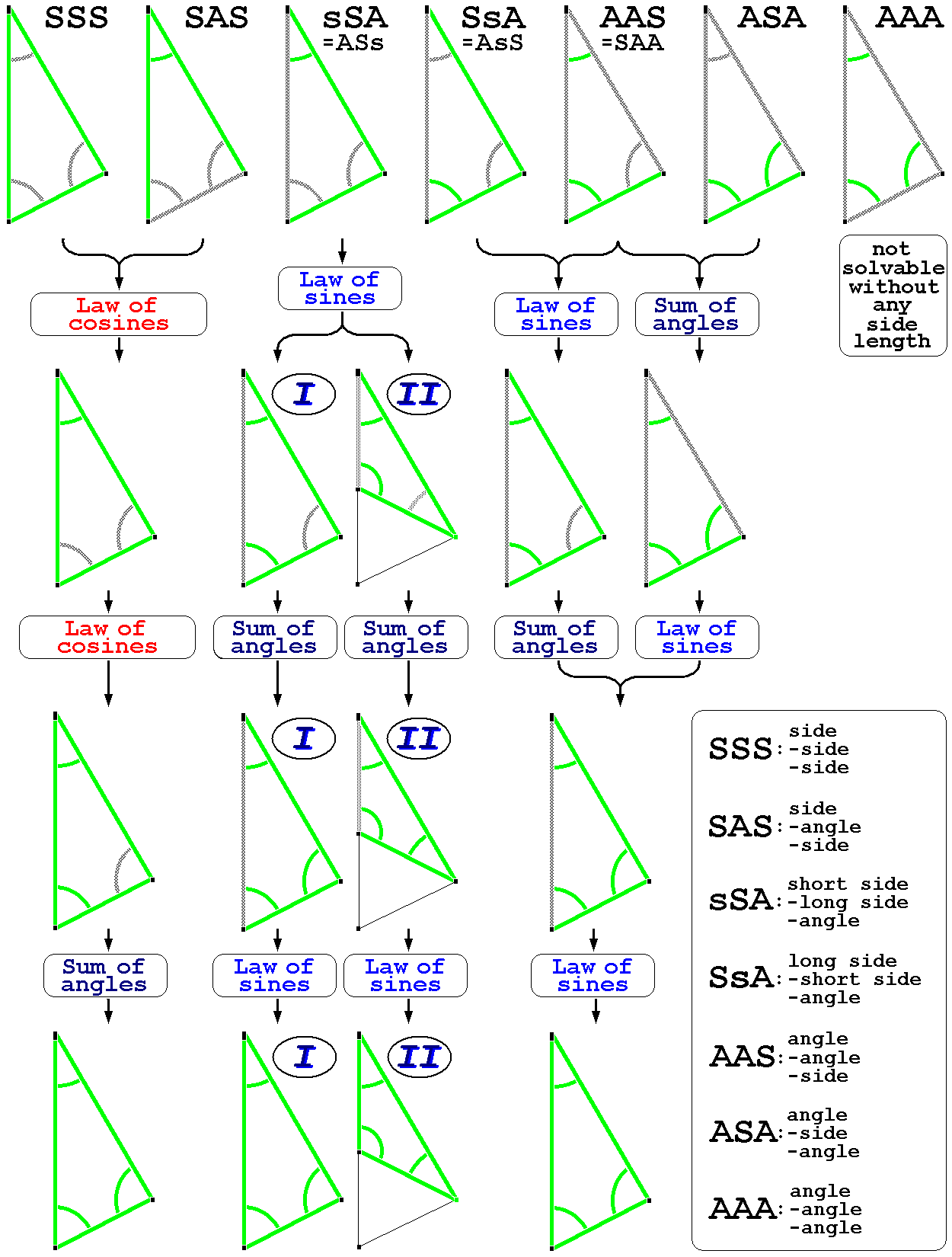
Solution Of Triangles
Solution of triangles () is the main trigonometric problem of finding the characteristics of a triangle (angles and lengths of sides), when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation. Solving plane triangles A general form triangle has six main characteristics (see picture): three linear (side lengths ) and three angular (). The classical plane trigonometry problem is to specify three of the six characteristics and determine the other three. A triangle can be uniquely determined in this sense when given any of the following: *Three sides (SSS) *Two sides and the included angle (SAS, side-angle-side) *Two sides and an angle not included between them (SSA), if the side length adjacent to the angle is shorter than the other side length. *A side and the two angles adjacent to it (ASA) *A side, the angle opposite to it and an angle adjacent to it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |