|
Elasticity (physics)
In physics and materials science, elasticity is the ability of a body to resist a distorting influence and to return to its original size and shape when that influence or force is removed. Solid objects will deform when adequate loads are applied to them; if the material is elastic, the object will return to its initial shape and size after removal. This is in contrast to ''plasticity'', in which the object fails to do so and instead remains in its deformed state. The physical reasons for elastic behavior can be quite different for different materials. In metals, the Crystal structure, atomic lattice changes size and shape when forces are applied (energy is added to the system). When forces are removed, the lattice goes back to the original lower energy state. For rubber elasticity, rubbers and other polymers, elasticity is caused by the stretching of polymer chains when forces are applied. Hooke's law states that the force required to deform elastic objects should be Prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Mechanics
Solid mechanics (also known as mechanics of solids) is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation (mechanics), deformation under the action of forces, temperature changes, phase (chemistry), phase changes, and other external or internal agents. Solid mechanics is fundamental for civil engineering, civil, Aerospace engineering, aerospace, nuclear engineering, nuclear, Biomedical engineering, biomedical and mechanical engineering, for geology, and for many branches of physics and chemistry such as materials science. It has specific applications in many other areas, such as understanding the anatomy of living beings, and the design of dental prosthesis, dental prostheses and surgical implants. One of the most common practical applications of solid mechanics is the Euler–Bernoulli beam theory, Euler–Bernoulli beam equation. Solid mechanics extensively uses tensors to describe stresses, strains, and the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young's Modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio of the stress (force per unit area) applied to the object and the resulting axial strain (displacement or deformation) in the linear elastic region of the material. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experiments that used the concept of Young's modulus in its modern form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years. The term modulus is derived from the Latin root term '' modus'', which means ''measure''. Definition Young's modulus, E, quantifies the relationship between tensile or compressive stress \sigma (force per unit ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain (engineering)
In engineering, deformation (the change in size or shape of an object) may be ''elastic'' or ''plastic''. If the deformation is negligible, the object is said to be ''rigid''. Main concepts Occurrence of deformation in engineering applications is based on the following background concepts: * ''Displacements'' are any change in position of a point on the object, including whole-body translations and rotations ( rigid transformations). * ''Deformation'' are changes in the relative position between internals points on the object, excluding rigid transformations, causing the body to change shape or size. * ''Strain'' is the ''relative'' ''internal'' deformation, the dimensionless change in shape of an infinitesimal cube of material relative to a reference configuration. Mechanical strains are caused by mechanical stress, ''see stress-strain curve''. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while ''strain'' is the measure of the relative deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
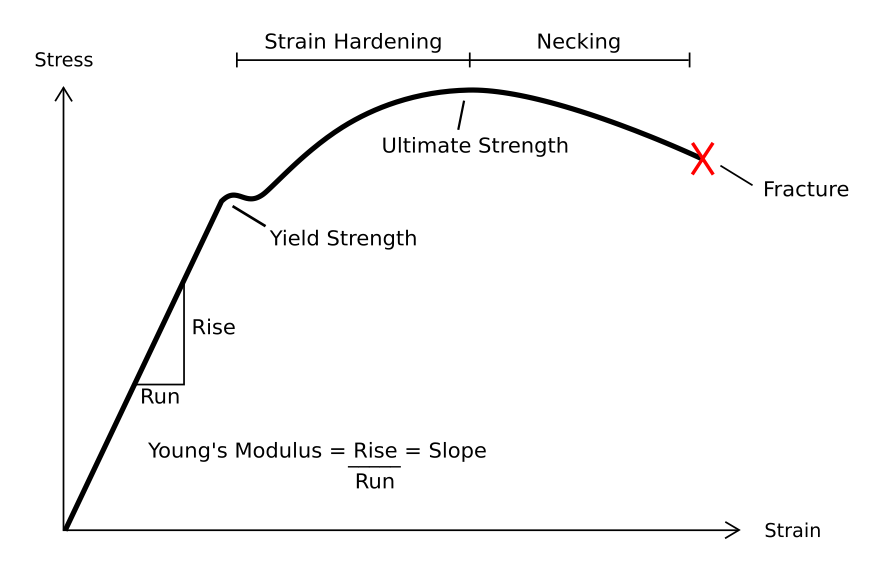
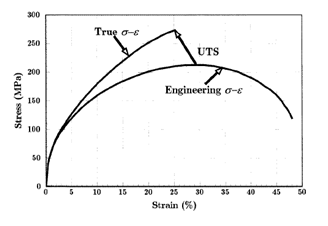
Stress–strain Curve
In engineering and materials science, a stress–strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined (see tensile testing). These curves reveal many of the properties of a material, such as the Young's modulus, the yield strength and the ultimate tensile strength. Definition Generally speaking, curves that represent the relationship between stress and strain in any form of deformation can be regarded as stress–strain curves. The stress and strain can be normal, shear, or a mixture, and can also be uniaxial, biaxial, or multiaxial, and can even change with time. The form of deformation can be compression, stretching, torsion, rotation, and so on. If not mentioned otherwise, stress–strain curve typically refers to the relationship between axial normal stress and axial normal strain of materials measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shearing (physics)
In continuum mechanics, shearing refers to the occurrence of a shear strain, which is a deformation of a material substance in which parallel internal surfaces slide past one another. It is induced by a shear stress in the material. Shear strain is distinguished from volumetric strain. The change in a material's volume in response to stress and change of angle is called the angle of shear. Overview Often, the verb ''shearing'' refers more specifically to a mechanical process that causes a plastic shear strain in a material, rather than causing a merely elastic one. A plastic shear strain is a continuous (non-fracturing) deformation that is irreversible, such that the material does not recover its original shape. It occurs when the material is yielding. The process of shearing a material may induce a volumetric strain along with the shear strain. In soil mechanics, the volumetric strain associated with shearing is known as Reynolds' dilation if it increases the volume, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. Definition The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Elastic constants and moduli Elastic constants are specific parameters that quantify the stiffness of a material in response to applied stresses and are fundamental in defining the elastic pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yield Strength
In materials science and engineering, the yield point is the point on a stress–strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation. The yield strength or yield stress is a material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable load in a mechanical component, since it represents the upper limit to forces that can be applied without producing permanent deformation. For most metals, such as aluminium and cold-worked steel, there is a gradual onset of non-linear behavior, and no precise yield point. In such a case, the offset yield p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal (unit)
The pascal (symbol: Pa) is the unit of pressure in the International System of Units (SI). It is also used to quantify internal pressure, stress, Young's modulus, and ultimate tensile strength. The unit, named after Blaise Pascal, is an SI coherent derived unit defined as one newton per square metre (N/m2). It is also equivalent to 10 barye (10 Ba) in the CGS system. Common multiple units of the pascal are the hectopascal (1 hPa = 100 Pa), which is equal to one millibar, and the kilopascal (1 kPa = 1000 Pa), which is equal to one centibar. The unit of measurement called '' standard atmosphere (atm)'' is defined as . Meteorological observations typically report atmospheric pressure in hectopascals per the recommendation of the World Meteorological Organization, thus a standard atmosphere (atm) or typical sea-level air pressure is about 1013 hPa. Reports in the United States typically use inches of mercury or millibars (hectopascals). In Cana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International System Of Units
The International System of Units, internationally known by the abbreviation SI (from French ), is the modern form of the metric system and the world's most widely used system of measurement. It is the only system of measurement with official status in nearly every country in the world, employed in science, technology, industry, and everyday commerce. The SI system is coordinated by the International Bureau of Weights and Measures, which is abbreviated BIPM from . The SI comprises a coherent system of units of measurement starting with seven base units, which are the second (symbol s, the unit of time), metre (m, length), kilogram (kg, mass), ampere (A, electric current), kelvin (K, thermodynamic temperature), mole (mol, amount of substance), and candela (cd, luminous intensity). The system can accommodate coherent units for an unlimited number of additional quantities. These are called coherent derived units, which can always be represented as products of powers of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (engineering)
In engineering, deformation (the change in size or shape of an object) may be ''elastic'' or ''plastic''. If the deformation is negligible, the object is said to be ''rigid''. Main concepts Occurrence of deformation in engineering applications is based on the following background concepts: * ''Displacements'' are any change in position of a point on the object, including whole-body translations and rotations ( rigid transformations). * ''Deformation'' are changes in the relative position between internals points on the object, excluding rigid transformations, causing the body to change shape or size. * ''Strain'' is the ''relative'' ''internal'' deformation, the dimensionless change in shape of an infinitesimal cube of material relative to a reference configuration. Mechanical strains are caused by mechanical stress, ''see stress-strain curve''. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |