|
Divisor Sum
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder. Definition An integer is divisible by a nonzero integer if there exists an integer such that n=km. This is written as :m\mid n. Other ways of saying the same thing are that divides , is a divisor of , is a factor of , and is a multiple of . If does not divide , then the notation is m\not\mid n. Usually, is required to be nonzero, but is allowed to be zero. With this convention, m \mid 0 for every nonzero integer . Some definitions omit the requirement that m be nonzero. General Divisors can be negative as well as positive, although sometimes the term is restricted to positive divisors. For example, there are six divisors of 4; they are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuisenaire Ten
Cuisenaire rods are mathematics learning aids for students that provide an interactive, hands-on way to explore mathematics and learn mathematical concepts, such as the four basic arithmetical operations, working with fractions and finding divisors. In the early 1950s, Caleb Gattegno popularised this set of coloured number rods created by Georges Cuisenaire (1891–1975), a Belgan primary school teacher, who called the rods ''réglettes''. According to Gattegno, "Georges Cuisenaire showed in the early 1950s that students who had been taught traditionally, and were rated 'weak', took huge strides when they shifted to using the material. They became 'very good' at traditional arithmetic when they were allowed to manipulate the rods." History The educationalists Maria Montessori and Friedrich Fröbel had used rods to represent numbers, but it was Georges Cuisenaire who introduced the rods that were to be used across the world from the 1950s onwards. In 1952 he published ''Les nombre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid's Lemma
In algebra and number theory, Euclid's lemma is a lemma that captures a fundamental property of prime numbers, namely: For example, if , , , then , and since this is divisible by 19, the lemma implies that one or both of 133 or 143 must be as well. In fact, . If the premise of the lemma does not hold, i.e., is a composite number, its consequent may be either true or false. For example, in the case of , , , composite number 10 divides , but 10 divides neither 4 nor 15. This property is the key in the proof of the fundamental theorem of arithmetic. It is used to define prime elements, a generalization of prime numbers to arbitrary commutative rings. Euclid's Lemma shows that in the integers irreducible elements are also prime elements. The proof uses induction so it does not apply to all integral domains. Formulations Euclid's lemma is commonly used in the following equivalent form: Euclid's lemma can be generalized as follows from prime numbers to any integers. This is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partially Ordered Set
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-negative
In mathematics, the sign of a real number is its property of being either positive, negative, or zero. Depending on local conventions, zero may be considered as being neither positive nor negative (having no sign or a unique third sign), or it may be considered both positive and negative (having both signs). Whenever not specifically mentioned, this article adheres to the first convention. In some contexts, it makes sense to consider a signed zero (such as floating-point representations of real numbers within computers). In mathematics and physics, the phrase "change of sign" is associated with the generation of the additive inverse (negation, or multiplication by −1) of any object that allows for this construction, and is not restricted to real numbers. It applies among other objects to vectors, matrices, and complex numbers, which are not prescribed to be only either positive, negative, or zero. The word "sign" is also often used to indicate other binary aspects of mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Highly Composite Number
__FORCETOC__ A highly composite number is a positive integer with more divisors than any smaller positive integer has. The related concept of largely composite number refers to a positive integer which has at least as many divisors as any smaller positive integer. The name can be somewhat misleading, as the first two highly composite numbers (1 and 2) are not actually composite numbers; however, all further terms are. The late mathematician Jean-Pierre Kahane has suggested that Plato must have known about highly composite numbers as he deliberately chose 5040 as the ideal number of citizens in a city as 5040 has more divisors than any numbers less than it. Ramanujan wrote and titled his paper on the subject in 1915. Examples The initial or smallest 38 highly composite numbers are listed in the table below . The number of divisors is given in the column labeled ''d''(''n''). Asterisks indicate superior highly composite numbers. The divisors of the first 15 highly composite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
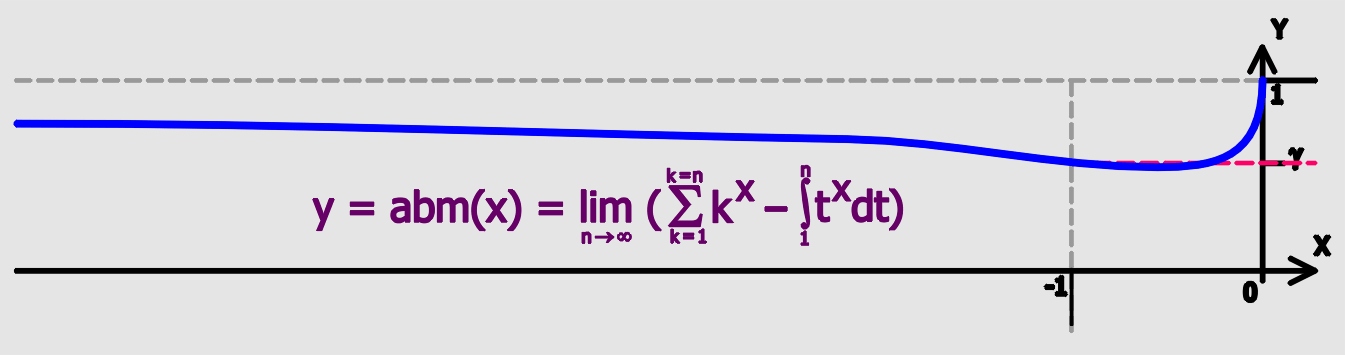
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization. When the numbers are sufficiently large, no efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty of this problem is important for the algorithms used in cryptography such as RSA public-key encryption and the RSA digital signature. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing. In 2019, Fabrice Boudot, Pierrick Gaudry, Aurore Guillevic, Nadia Heninger, Emmanuel Thomé and Paul Zimmermann factored a 240-digit (795-bit) number ( RSA-240) utilizing approximately 900 core-years of computing power. The researchers estimated that a 1024-bit R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function σ''z''(''n''), for a real or complex number ''z'', is defined as the sum of the ''z''th powers of the positive divisors of ''n''. It can be expressed in sigma notation as :\sigma_z(n)=\sum_ d^z\,\! , where is shorthand for "''d' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relatively Prime
In mathematics, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also '' is prime to '' or '' is coprime with ''. The numbers 8 and 9 are coprime, despite the fact that neither considered individually is a prime number, since 1 is their only common divisor. On the other hand, 6 and 9 are not coprime, because they are both divisible by 3. The numerator and denominator of a reduced fraction are coprime, by definition. Notation and testing Standard notations for relatively prime integers and are: and . In their 1989 textbook ''Concrete Mathematics'', Ronald Graham, Donald Knuth, and Oren Patashnik proposed that the notation a\perp b be used to indicate that and are relatively prime and that the term "prime" be used instead of coprime (a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Function
In number theory, a multiplicative function is an arithmetic function ''f''(''n'') of a positive integer ''n'' with the property that ''f''(1) = 1 and f(ab) = f(a)f(b) whenever ''a'' and ''b'' are coprime. An arithmetic function ''f''(''n'') is said to be completely multiplicative (or totally multiplicative) if ''f''(1) = 1 and ''f''(''ab'') = ''f''(''a'')''f''(''b'') holds ''for all'' positive integers ''a'' and ''b'', even when they are not coprime. Examples Some multiplicative functions are defined to make formulas easier to write: * 1(''n''): the constant function, defined by 1(''n'') = 1 (completely multiplicative) * Id(''n''): identity function, defined by Id(''n'') = ''n'' (completely multiplicative) * Id''k''(''n''): the power functions, defined by Id''k''(''n'') = ''n''''k'' for any complex number ''k'' (completely multiplicative). As special cases we have ** Id0(''n'') = 1(''n'') and ** Id1(''n'') = Id(''n''). * ''ε''(''n''): the function defined by ''ε''(''n' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abundant Number
In number theory, an abundant number or excessive number is a number for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example. Definition A number ''n'' for which the ''sum'' ''of'' ''divisors'' ''σ''(''n'') > 2''n'', or, equivalently, the sum of proper divisors (or aliquot sum) ''s''(''n'') > ''n''. Abundance is the value ''σ''(''n'') − ''2n'' (or ''s''(''n'') − ''n''). Examples The first 28 abundant numbers are: :12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, ... . For example, the proper divisors of 24 are 1, 2, 3, 4, 6, 8, and 12, whose sum is 36. Because 36 is greater than 24, the number 24 is abundant. Its abundance is 36 − 24 = 12. Prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deficient Number
In number theory, a deficient number or defective number is a number ''n'' for which the sum of divisors of ''n'' is less than 2''n''. Equivalently, it is a number for which the sum of proper divisors (or aliquot sum) is less than ''n''. For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient. Denoting by ''σ''(''n'') the sum of divisors, the value 2''n'' − ''σ''(''n'') is called the number's deficiency. In terms of the aliquot sum ''s''(''n''), the deficiency is ''n'' − ''s''(''n''). Examples The first few deficient numbers are :1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 45, 46, 47, 49, 50, ... As an example, consider the number 21. Its divisors are 1, 3, 7 and 21, and their sum is 32. Because 32 is less than 42, the number 21 is deficient. Its deficiency is 2 × 21 − 32 = 10. Properties Since the aliquot s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |