|
Disphenoid Tetrahedral Honeycomb
The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an ''oblate tetrahedrille'' or shortened to ''obtetrahedrille''. Symmetry of Things, Table 21.1. Prime Architectonic and Catopric tilings of space, p. 293, 295. A cell can be seen as 1/12 of a translational cube, with its vertices centered on two faces and two edges. Four of its edges belong to 6 cells, and two edges belong to 4 cells. : The tetrahedral disphenoid honeycomb is the dual of the uniform bitruncated cubic honeycomb. Its vertices form the A / D lattice, which is also known as the body-centered cubic lattice. Geometry This honeycomb's vertex figure is a tetrakis cube: 24 disphenoids meet at each vertex. The union of these 24 disphenoids forms a rhombic dodecahedron. Each edge of the tessellation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or ''close packing'' of polyhedron, polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean geometry, Euclidean ("flat") space. They may also be constructed in non-Euclidean geometry, non-Euclidean spaces, such as #Hyperbolic honeycombs, hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of cube, cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a Self-dual tessellation, self-dual tessellation with Schläfli symbol . John Horton Conway called this honeycomb a cubille. Description The cubic honeycomb is a space-filling or three-dimensional tessellation consisting of many cubes that attach each other to the faces; the cube is known as Cell (geometry), cell of a honeycomb. The parallelepiped is the member of a parallelohedron, generated from three line segments that are not all parallel to a common plane. The cube is the special case of a parallelepiped for having the most symmetric form, generated by three perpendicular unit-length line segments. In three-dimensional space, the cubic honeycomb is the only proper regular space-f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
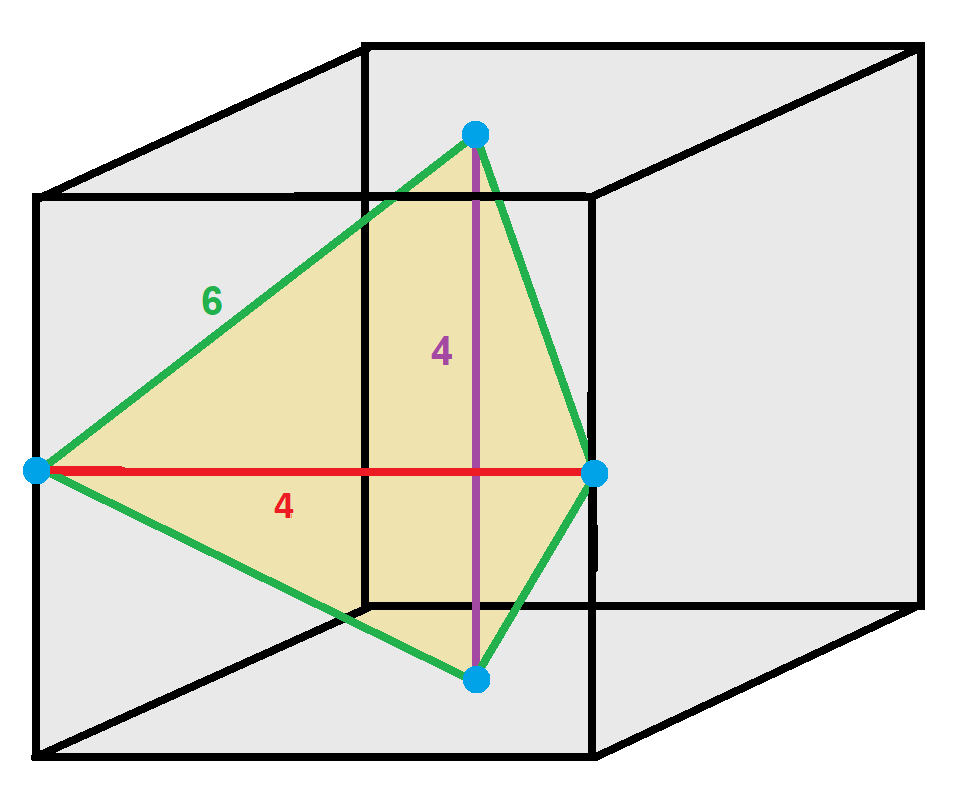
Disphenoid Tetrah Hc
In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron,. sphenoid,. bisphenoid, isosceles tetrahedron,. equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron. All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and its edges have three different lengths. Special cases and generalizations If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with Td tetrahedral symmetry, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles triangles, it is called a tetragonal disphenoid. In this c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonal Trapezohedron
In geometry, a trigonal trapezohedron is a polyhedron with six congruent quadrilateral faces, which may be scalene or rhomboid. The variety with rhombus-shaped faces faces is a rhombohedron. An alternative name for the same shape is the ''trigonal deltohedron''. Geometry Six identical rhombic faces can construct two configurations of trigonal trapezohedra. The ''acute'' or ''prolate'' form has three acute angle corners of the rhombic faces meeting at the two polar axis vertices. The ''obtuse'' or ''oblate'' or ''flat'' form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices. More strongly than having all faces congruent, the trigonal trapezohedra are isohedral figures, meaning that they have symmetries that take any face to any other face. Special cases A cube is a special case of a trigonal trapezohedron, since a square is a special case of a rhombus. A gyroelongated triangular bipyramid constructed with equilateral triangles can al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. Three equivalent definitions of ''parallelepiped'' are *a hexahedron with three pairs of parallel faces, *a polyhedron with six faces (hexahedron), each of which is a parallelogram, and *a prism (geometry), prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all special cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; traditionally it was because of its etymology in Ancient Greek, Greek παραλληλεπίπεδον ''parallelepipedon'' (with short -i-), a body "having parallel planes". Parallelepipeds are a subclass of the prismatoids. Properties Any of the three pairs of parallel faces can be viewed as the bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 types. As a Catalan solid, it is the dual polyhedron of the cuboctahedron. As a parallelohedron, the rhombic dodecahedron can be used to Honeycomb (geometry), tesselate its copies in space creating a rhombic dodecahedral honeycomb. There are some variations of the rhombic dodecahedron, one of which is the Bilinski dodecahedron. There are some stellations of the rhombic dodecahedron, one of which is the Escher's solid. The rhombic dodecahedron may also appear in nature (such as in the garnet crystal), the architectural philosophies, practical usages, and toys. As a Catalan solid Metric properties The rhombic dodecahedron is a polyhedron with twelve rhombus, rhombi, each of which long face-diagonal length is exactly \sqrt times the sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrakis Cube
In geometry, a tetrakis hexahedron (also known as a tetrahexahedron, hextetrahedron, tetrakis cube, and kiscube) is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be called a disdyakis hexahedron or hexakis tetrahedron as the dual of an omnitruncated tetrahedron, and as the barycentric subdivision of a tetrahedron. As a Kleetope The name "tetrakis" is used for the Kleetopes of polyhedra with square faces. Hence, the tetrakis hexahedron can be considered as a cube with square pyramids covering each square face, the Kleetope of the cube. The resulting construction can be either convex or non-convex, depending on the square pyramids' height. For the convex result, it comprises twenty-four isosceles triangles. A non-convex form of this shape, with equilateral triangle faces, has the same surface geometry as the regular octahedron, and a paper octahedron model can be re-folded into this shape. This form of the tetrakis hexahedron was illustr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tessellation, tilings or, by extension, to Honeycomb (geometry), space-filling tessellation with polytope Cell (geometry), cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges conn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc) Note: the term fcc is often used in synonym for the ''cubic close-packed'' or ccp structure occurring in metals. However, fcc stands for a face-centered cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais latices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated Cubic Honeycomb
The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of truncated octahedron, truncated octahedra (or, equivalently, Bitruncation (geometry), bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedron, truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 Convex uniform honeycomb, uniform honeycombs. John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an ''oblate tetrahedrille'', also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces. Geometry It can be realized as the Voronoi tessellation of the body-centred cubic lattice. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |