|
Diffusion Theory
Photon transport in biological tissue can be equivalently modeled numerically with Photon transport monte carlo, Monte Carlo simulations or analytically by the radiative transfer equation (RTE). However, the RTE is difficult to solve without introducing approximations. A common approximation summarized here is the diffusion approximation. Overall, solutions to the diffusion equation for photon transport are more computationally efficient, but less accurate than Monte Carlo simulations. Definitions The RTE can mathematically model the transfer of energy as photons move inside a tissue. The flow of radiation energy through a small area element in the radiation field can be characterized by radiance L(\vec,\hat,t) with units \frac. Radiance is defined as energy flow per unit normal area per unit solid angle per unit time. Here, \vec denotes position, \hat denotes unit direction vector and t denotes time (Figure 1). Several other important physical quantities are based on the defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photon Transport Monte Carlo
Modeling photon propagation with Monte Carlo methods is a flexible yet rigorous approach to simulate photon transport. In the method, local rules of photon transport are expressed as probability distributions which describe the step size of photon movement between sites of photon-matter interaction and the angles of deflection in a photon's trajectory when a scattering event occurs. This is equivalent to modeling photon transport analytically by the Radiative transfer equation and diffusion theory for photon transport in biological tissue, radiative transfer equation (RTE), which describes the motion of photons using a differential equation. However, closed-form solutions of the RTE are often not possible; for some geometries, the Radiative transfer equation and diffusion theory for photon transport in biological tissue, diffusion approximation can be used to simplify the RTE, although this, in turn, introduces many inaccuracies, especially near sources and boundaries. In contrast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiation) in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called ''diffuse reflections'' and unscattered reflections are called ''specular'' (mirror-like) reflections. Originally, the term was confined to light scattering (going back at least as far as Isaac Newton in the 17th century). As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" (not then recognized as electromagnetic in nature) in 1800. John Tyndall, a pioneer in light scattering research, noted the connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Coefficient
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fick's Law
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. ''Fick's first law'': Movement of particles from high to low concentration (diffusive flux) is directly proportional to the particle's concentration gradient. ''Fick's second law'': Prediction of change in concentration gradient with time due to diffusion. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Free Path
In physics, mean free path is the average distance over which a moving particle (such as an atom, a molecule, or a photon) travels before substantially changing its direction or energy (or, in a specific context, other properties), typically as a result of one or more successive collisions with other particles. Scattering theory Imagine a beam of particles being shot through a target, and consider an infinitesimally thin slab of the target (see the figure). The atoms (or particles) that might stop a beam particle are shown in red. The magnitude of the mean free path depends on the characteristics of the system. Assuming that all the target particles are at rest but only the beam particle is moving, that gives an expression for the mean free path: :\ell = (\sigma n)^, where is the mean free path, is the number of target particles per unit volume, and is the effective cross-sectional area for collision. The area of the slab is , and its volume is . The typical number of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radiant Exposure
In radiometry, radiant exposure or fluence is the radiant energy ''received'' by a ''surface'' per unit area, or equivalently the irradiance of a ''surface,'' integrated over time of irradiation, and spectral exposure is the radiant exposure per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The SI unit of radiant exposure is the joule per square metre (), while that of spectral exposure in frequency is the joule per square metre per hertz () and that of spectral exposure in wavelength is the joule per square metre per metre ()—commonly the joule per square metre per nanometre (). Mathematical definitions Radiant exposure Radiant exposure of a ''surface'', denoted ''H''e ("e" for "energetic", to avoid confusion with photometric quantities), is defined as H_\mathrm = \frac = \int_0^T E_\mathrm(t)\, \mathrmt, where *∂ is the partial derivative symbol; *''Q''e is the radiant energy; *''A'' is the area; *''T'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Harmonics
In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics. Since the spherical harmonics form a complete set of orthogonal functions and thus an orthonormal basis, every function defined on the surface of a sphere can be written as a sum of these spherical harmonics. This is similar to periodic functions defined on a circle that can be expressed as a sum of circular functions (sines and cosines) via Fourier series. Like the sines and cosines in Fourier series, the spherical harmonics may be organized by (spatial) angular frequency, as seen in the rows of functions in the illustration on the right. Further, spherical harmonics are basis functions for irreducible representations of SO(3), the group of rotations in three dimensions, and thus play a cen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
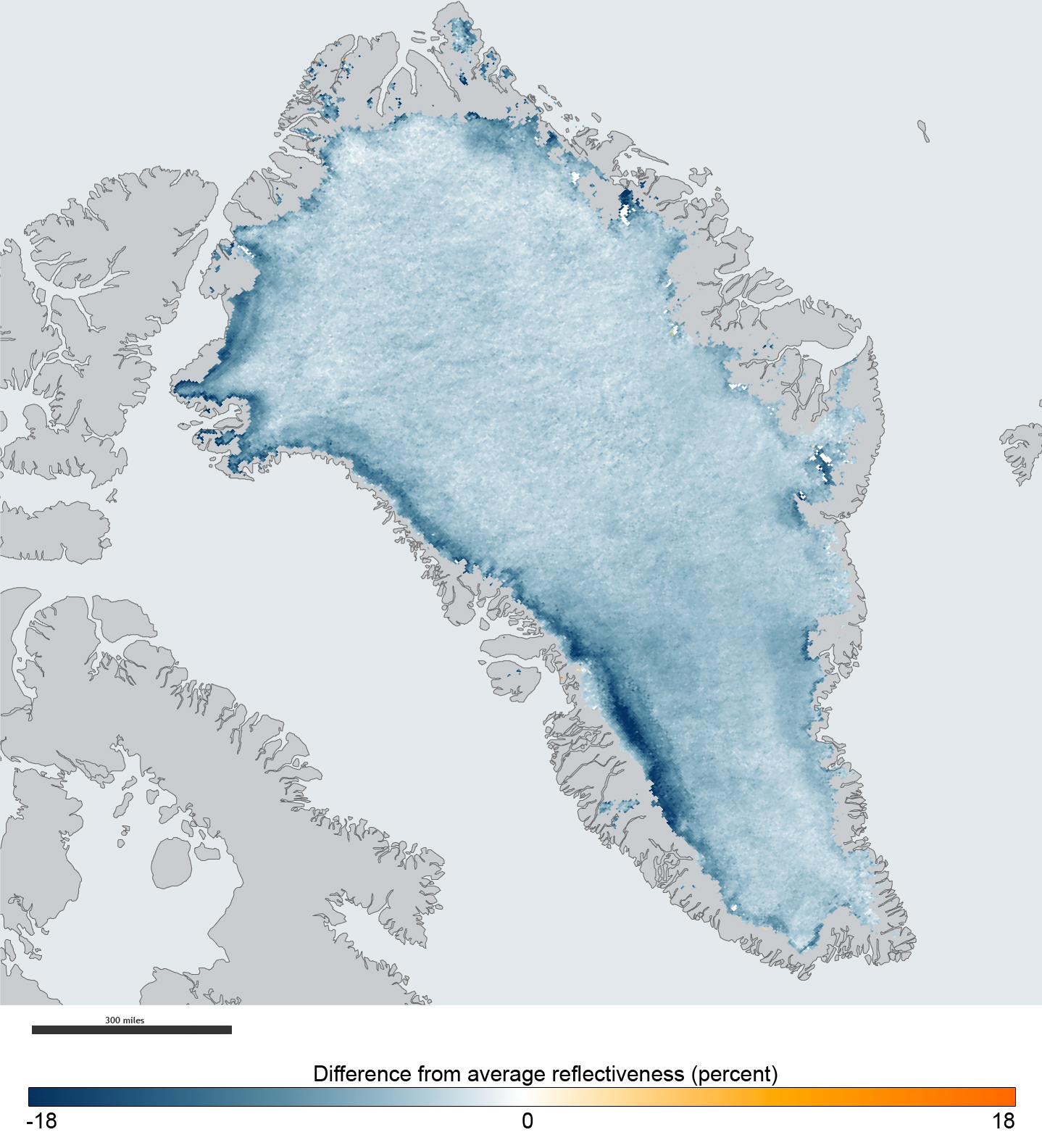
Albedo
Albedo ( ; ) is the fraction of sunlight that is Diffuse reflection, diffusely reflected by a body. It is measured on a scale from 0 (corresponding to a black body that absorbs all incident radiation) to 1 (corresponding to a body that reflects all incident radiation). ''Surface albedo'' is defined as the ratio of Radiosity (radiometry), radiosity ''J''e to the irradiance ''E''e (flux per unit area) received by a surface. The proportion reflected is not only determined by properties of the surface itself, but also by the spectral and angular distribution of solar radiation reaching the Earth's surface. These factors vary with atmospheric composition, geographic location, and time (see position of the Sun). While directional-hemispherical reflectance factor is calculated for a single angle of incidence (i.e., for a given position of the Sun), albedo is the directional integration of reflectance over all solar angles in a given period. The temporal resolution may range from seconds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photon Diffusion
Photon diffusion is a situation where photons travel through a material without being absorbed, but rather undergoing repeated scattering events which change the direction of their path. The path of any given photon is then effectively a random walk. A large ensemble of such photons can be said to exhibit diffusion in the material, and can be described with a diffusion equation. Astrophysics In astrophysics, photon diffusion occurs inside a stellar atmosphere. To describe this phenomenon, one should develop the transfer equation in moments and use the Eddington approximation to radiative transfer (i.e. the diffusion approximation). In 3D the results are two equations for the photon energy flux: :\vec F = -\frac\vec \nabla U, :\vec \nabla \cdot \vec F = 0, where \sigma is the opacity. By substituting the first equation into the second, one obtains the diffusion equation for the photon energy density: :\nabla^2 U -\frac\vec \nabla U \cdot \vec \nabla \sigma=0. Medical science In me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Coordinate System
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are * the radial distance along the line connecting the point to a fixed point called the origin; * the polar angle between this radial line and a given ''polar axis''; and * the azimuthal angle , which is the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (''r'', ''θ'', ''φ''), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the ''reference plane'' (sometimes '' fundamental plane''). Terminology The radial distance from the fixed point of origin is also called the ''radius'', or ''radial line'', or ''radial coor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Of Light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time interval of second. The speed of light is invariant (physics), the same for all observers, no matter their relative velocity. It is the upper limit for the speed at which Information#Physics_and_determinacy, information, matter, or energy can travel through Space#Relativity, space. All forms of electromagnetic radiation, including visible light, travel at the speed of light. For many practical purposes, light and other electromagnetic waves will appear to propagate instantaneously, but for long distances and sensitive measurements, their finite speed has noticeable effects. Much starlight viewed on Earth is from the distant past, allowing humans to study the history of the universe by viewing distant objects. When Data communication, comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Equation
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium; it was devised by Ludwig Boltzmann in 1872.Encyclopaedia of Physics (2nd Edition), R. G. Lerner, G. L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3. The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number. The equation arises not by analyzing the individual positions and momenta of each particle in the fluid but rather by considering a probability distribution for the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |