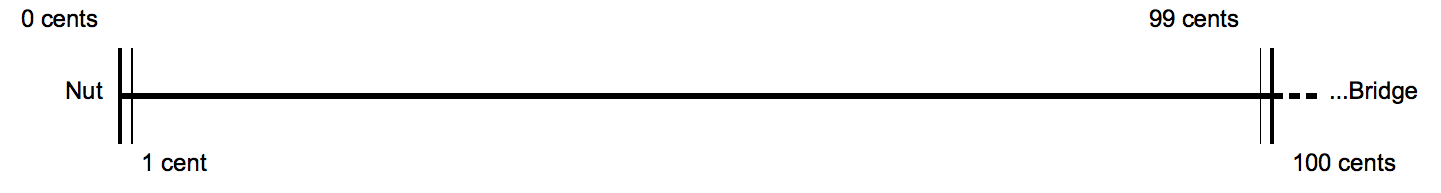|
Diesis
In classical music from Western culture, a diesis ( , plural dieses ( , "difference"; Greek: δίεσις "leak" or "escape"Benson, Dave (2006). ''Music: A Mathematical Offering'', p.171. . Based on the technique of playing the aulos, where pitch is raised a small amount by slightly raising the finger on the lowest closed hole, letting a small amount of air "escape".) is either an accidental (see sharp), or a very small musical interval, usually defined as the difference between an octave (in the ratio 2:1) and three justly tuned major thirds (tuned in the ratio 5:4), equal to 128:125 or about 41.06 cents. In 12-tone equal temperament (on a piano for example) three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C', and three justly tuned major thirds (5:4) span from C to B (namely, from C, to E, to G, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diesis On C
In classical music from Western culture, a diesis ( , plural dieses ( , "difference"; Greek: δίεσις "leak" or "escape"Benson, Dave (2006). ''Music: A Mathematical Offering'', p.171. . Based on the technique of playing the aulos, where pitch is raised a small amount by slightly raising the finger on the lowest closed hole, letting a small amount of air "escape".) is either an accidental (see sharp), or a very small musical interval, usually defined as the difference between an octave (in the ratio 2:1) and three justly tuned major thirds (tuned in the ratio 5:4), equal to 128:125 or about 41.06 cents. In 12-tone equal temperament (on a piano for example) three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C', and three justly tuned major thirds (5:4) span from C to B (namely, from C, to E, to G, to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lesser Diesis (difference M2-A1)
In classical music from Western culture, a diesis ( , plural dieses ( , "difference"; Greek: δίεσις "leak" or "escape"Benson, Dave (2006). ''Music: A Mathematical Offering'', p.171. . Based on the technique of playing the aulos, where pitch is raised a small amount by slightly raising the finger on the lowest closed hole, letting a small amount of air "escape".) is either an accidental (see sharp), or a very small musical interval, usually defined as the difference between an octave (in the ratio 2:1) and three justly tuned major thirds (tuned in the ratio 5:4), equal to 128:125 or about 41.06 cents. In 12-tone equal temperament (on a piano for example) three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C', and three justly tuned major thirds (5:4) span from C to B (namely, from C, to E, to G, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comma (music)
In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word ''comma'' used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning system, and another F tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B and A are both approximated by the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sharp (music)
In music, sharp, dièse (from French), or diesis (from Greek) means, "higher in pitch". More specifically, in musical notation, sharp means "higher in pitch by one semitone (half step)". Sharp is the opposite of flat, which is a lowering of pitch. A sharp symbol, , is used in key signatures or as an accidental. For instance, the music below has a key signature with three sharps (indicating either A major or F minor, the relative minor) and the note, A, has a sharp accidental. : Under twelve-tone equal temperament, B, for instance, sounds the same as, or is enharmonically equivalent to, C natural (C), and E is enharmonically equivalent to F. In other tuning systems, such enharmonic equivalences in general do not exist. To allow extended just intonation, composer Ben Johnston uses a sharp to indicate a note is raised 70.6 cents (ratio 25:24), or a flat to indicate a note is lowered 70.6 cents. In intonation, sharp can also mean "slightly higher in pitch" (by som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Treatise On Harmony
A treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject and its conclusions."Treatise." Merriam-Webster Online Dictionary. Accessed September 12, 2020. A monograph is a treatise on a specialized topic. Etymology The word 'treatise' first appeared in the fourteenth century as the Medieval English word ''tretis'', which evolved from the Medieval Latin ''tractatus'' and the Latin ''tractare'', meaning to treat or to handle. Historically significant treatises Table The works presented here have been identified as influential by scholars on the development of human civilization. Discussion of select examples Euclid's ''Elements'' Euclid's ''Elements'' has appeared in more editions than any other books except the ''Bible'' and is one of the most important mathematical treatises ever. It has been translated to nume ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rameau
Jean-Philippe Rameau (; – ) was a French composer and music theorist. Regarded as one of the most important French composers and music theorists of the 18th century, he replaced Jean-Baptiste Lully as the dominant composer of French opera and is also considered the leading French composer of his time for the harpsichord, alongside François Couperin. Little is known about Rameau's early years. It was not until the 1720s that he won fame as a major theorist of music with his '' Treatise on Harmony'' (1722) and also in the following years as a composer of masterpieces for the harpsichord, which circulated throughout Europe. He was almost 50 before he embarked on the operatic career on which his reputation chiefly rests today. His debut, '' Hippolyte et Aricie'' (1733), caused a great stir and was fiercely attacked by the supporters of Lully's style of music for its revolutionary use of harmony. Nevertheless, Rameau's pre-eminence in the field of French opera was soon acknowle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limma
The word limma or leimma (from Greek: λείμμα, ''leimma''; meaning "remnant") can refer to several different musical intervals, whose only common property is their small size. :More specifically, in Pythagorean tuning (i.e. 3-limit): :*The original Pythagorean limma, 256/243, a Pythagorean interval (). :and in 5-limit tuning: :*The 5-limit diatonic semitone, 16/15 (). Although closer in size to the Pythagorean apotome than to the limma, it has been so called because of its function as a diatonic semitone rather than a chromatic one. :*The 5-limit limma (now a diesis), 128/125, the amount by which three just major thirds fall short of an octave (). :*The major limma, 135/128, which is the difference between two major whole tones and a minor third In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philolaus
Philolaus (; grc, Φιλόλαος, ''Philólaos''; ) was a Greek Pythagorean and pre-Socratic philosopher. He was born in a Greek colony in Italy and migrated to Greece. Philolaus has been called one of three most prominent figures in the Pythagorean tradition and the most outstanding figure in the Pythagorean school. Pythagoras developed a school of philosophy that was dominated by both mathematics and mysticism. Most of what is known today about the Pythagorean astronomical system is derived from Philolaus's views. He may have been the first to write about Pythagorean doctrine. According to August Böckh (1819), who cites Nicomachus, Philolaus was the successor of Pythagoras. He argued that at the foundation of everything is the part played by the limiting and limitless, which combine in a harmony. With his assertions that the Earth was not the center of the universe ( geocentrism), he is credited with the earliest known discussion of concepts in the development of helioc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recte
The Latin adverb ''sic'' (; "thus", "just as"; in full: , "thus was it written") inserted after a quoted word or passage indicates that the quoted matter has been transcribed or translated exactly as found in the source text, complete with any erroneous, archaic, or otherwise nonstandard spelling, punctuation, or grammar. It also applies to any surprising assertion, faulty reasoning, or other matter that might be interpreted as an error of transcription. The typical usage is to inform the reader that any errors or apparent errors in quoted material do not arise from errors in the course of the transcription, but are intentionally reproduced, exactly as they appear in the source text. It is generally placed inside square brackets to indicate that it is not part of the quoted matter. ''Sic'' may also be inserted derisively or sarcastically, to call attention to the original writer's spelling mistakes or erroneous logic, or to show general disapproval or dislike of the material. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. . This ratio, also known as the " pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈702 cents wide. The system dates to Ancient Mesopotamia; see . The system is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


_-_001.jpg)